Fuerza entre dos cargas en movimiento

De Laplace

(Diferencias entre revisiones)

Revisión de 10:47 18 abr 2009

Contenido

1 Enunciado
2 Fuerza magnética
- 2.1 Directamente
- 2.2 Empleando el campo magnético
3 Comparación con la fuerza eléctrica
4 Cambio de signo
5 Velocidades perpendiculares
- 5.1 Directamente
- 5.2 Empleando el campo magnético
6 Observaciones

1 Enunciado

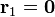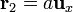Dos cargas puntuales iguales $q 1$ y $q 2$ se mueven con la misma celeridad $v$ de forma que en un instante se encuentran situadas en $\mathbf{r}_1=\mathbf{0}$ y $\mathbf{r}_2 = a\mathbf{u}_{x}$ , respectivamente.

Si las dos cargas se mueven con velocidades pequeñas 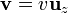$\mathbf{v} = v\mathbf{u}_{z}$ , calcule el valor aproximado de la fuerza eléctrica y de la fuerza magnética que ejerce cada carga sobre la otra. ¿Cuál es la proporción entre estas dos fuerzas?

¿Cómo cambian estas fuerzas si se cambia el signo de una de las cargas, el sentido de una de las velocidades, o ambas cosas a la vez?

Calcule el valor de estas fuerzas si 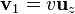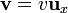$\mathbf{v}_1=v\mathbf{u}_{z}$ , $\mathbf{v}=v\mathbf{u}_{x}$ . ¿Se verifica la tercera ley de Newton?

2 Fuerza magnética

2.1 Directamente

Podemos hallar la fuerza magnética entre las dos cargas empleando la Ley de Biot y Savart para cargas puntuales. La fuerza que la carga 1 produce sobre la 2 es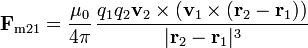 $\mathbf{F}_{\mathrm{m}21} = \frac{\mu_0}{4\pi}\,\frac{q_1q_2\mathbf{v}_2\times(\mathbf{v}_1\times(\mathbf{r}_2-\mathbf{r}_1))}{|\mathbf{r}_2-\mathbf{r}_1|^3}$

donde en nuestro caso tenemos, tomando como Z el que pasa por la carga 1 y paralelo a su velocidad, y como eje X el que va de la carga 1 a la 2,

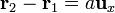
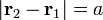
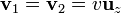
$\mathbf{r}_2-\mathbf{r}_1=a\mathbf{u}_x$ $|\mathbf{r}_2-\mathbf{r}_1|=a$ $\mathbf{v}_1=\mathbf{v}_2=v\mathbf{u}_z\,$

Sustituyendo nos queda

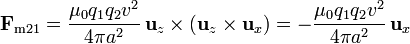
$\mathbf{F}_{\mathrm{m}21}= \frac{\mu_0q_1q_2v^2}{4\pi a^2}\,\mathbf{u}_z\times(\mathbf{u}_z\times\mathbf{u}_x) = -\frac{\mu_0q_1q_2v^2}{4\pi a^2}\,\mathbf{u}_x$

donde hemos usado los productos entre los vectores de la base. Esta fuerza sobre la carga 2 va en la dirección de la 1, es decir, es atractiva.

Para hallar la fuerza que la carga 2 produce sobre la 1, lo único que cambia es que el vector de posición relativo es ahora 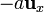$-a\mathbf{u}_x$ , por lo que resulta una fuerza

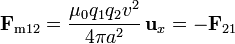
$\mathbf{F}_{\mathrm{m}12}=\frac{\mu_0q_1q_2v^2}{4\pi a^2}\,\mathbf{u}_x = -\mathbf{F}_{21}$

Esta fuerza es también atractiva, cumplie´ndose además la tercera ley de Newton.

Generalizando este resultado tenemos que las fuerzas entre corrientes paralelas y en el mismo sentido, son atractivas.

2.2 Empleando el campo magnético

Podemos escribir el resultado de una forma más clara, desglosando el cálculo con ayuda del campo magnético como intermediario. Consideramos que la carga 1 produce un campo magnético, que es percibido por la carga 2.

El campo magnético de la carga 1 en todo el espacio es

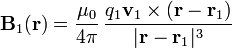
$\mathbf{B}_1(\mathbf{r})=\frac{\mu_0}{4\pi}\,\frac{q_1\mathbf{v}_1\times(\mathbf{r}-\mathbf{r}_1)}{|\mathbf{r}-\mathbf{r}_1|^3}$

y en la posición de la 2ª es

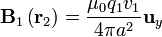
$\mathbf{B}_1\left(\mathbf{r}_2\right) = \frac{\mu _0q_1v_1}{4\pi a^2}\mathbf{u}_y$

La fuerza magnética sobre la carga 2, de acuerdo con la ley de Lorentz

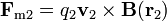
$\mathbf{F}_{\mathrm{m}2}=q_2\mathbf{v}_2\times\mathbf{B}(\mathbf{r}_2)$

que, sustituyendo el campo anterior nos da lo que ya conocemos

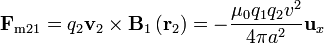
$\mathbf{F}_{\mathrm{m}21} = q_2\mathbf{v}_2 \times \mathbf{B}_1\left(\mathbf{r}_2\right) = - \frac{\mu _0q_1q_2v^2}{4\pi a^2}\mathbf{u}_x$

3 Comparación con la fuerza eléctrica

Podemos comparar la magnitud de esta fuerza con la fuerza eléctrica entre ambas cargas. Si la velocidad de las cargas es pequeña, podemos aproximar la fuerza mediante la ley de Coulomb:

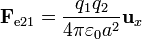
$\mathbf{F}_{\mathrm{e}21} = \frac{q_1q_2}{4\pi\varepsilon_0a^2}\mathbf{u}_x$

La proporción entre ambas fuerzas es

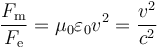
$\frac{F_\mathrm{m}}{F_\mathrm{e}}=\mu_0\varepsilon_0 v^2=\frac{v^2}{c^2}$

donde 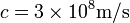$c = 3\times 10^{8}\mathrm{m}/\mathrm{s}$ es la velocidad de la luz. Por ello, normalmente

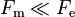
$F_\mathrm{m}\ll F_\mathrm{e}$

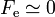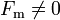Las fuerzas magnéticas sólo son apreciables porque la materia es neutra. En la interacción entre dos hilos conductores de corriente, las fuerzas eléctricas entre iones y electrones se cancelan (y $F_\mathrm{e}\simeq 0$ ). Para la fuerza magnética sólo cuentan los electrones móviles, y $F_\mathrm{m}\neq 0$ .

4 Cambio de signo

Si cambiamos el signo a una de las cargas la fuerza magnética cambia de signo, pasando a ser repulsiva. Lo mismo ocurre si cambiamos el sentido a una de las velocidades. Si cambiamos el signo de una carga y de una velocidad, la fuerza vuelve a ser atractiva.

Teniendo en cuenta que la densidad de corriente va como el producto de la carga por la velocidad, este resultado predice que corrientes paralelas (↑↑) se atraen, mientras que las antiparalelas (↑↓) se repelen.

5 Velocidades perpendiculares

5.1 Directamente

Aplicando de nuevo la expresión de la fuerza entre dos cargas en movimiento

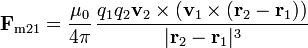
$\mathbf{F}_{\mathrm{m}21} = \frac{\mu_0}{4\pi}\,\frac{q_1q_2\mathbf{v}_2\times(\mathbf{v}_1\times(\mathbf{r}_2-\mathbf{r}_1))}{|\mathbf{r}_2-\mathbf{r}_1|^3}$

donde tenemos ahora, al igual que antes

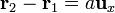
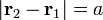
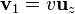
$\mathbf{r}_2-\mathbf{r}_1=a\mathbf{u}_x$ $|\mathbf{r}_2-\mathbf{r}_1|=a$ $\mathbf{v}_1=v\mathbf{u}_z\,$

siendo el único cambio

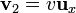
$\mathbf{v}_2=v\mathbf{u}_x\,$

que al sustituir nos da

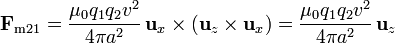
$\mathbf{F}_{\mathrm{m}21}= \frac{\mu_0q_1q_2v^2}{4\pi a^2}\,\mathbf{u}_x\times(\mathbf{u}_z\times\mathbf{u}_x) = \frac{\mu_0q_1q_2v^2}{4\pi a^2}\,\mathbf{u}_z$

Si hallamos ahora la fuerza que la 2 produce sobre la 1

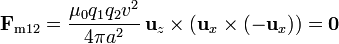
$\mathbf{F}_{\mathrm{m}12}= \frac{\mu_0q_1q_2v^2}{4\pi a^2}\,\mathbf{u}_z\times(\mathbf{u}_x\times(-\mathbf{u}_x)) =\mathbf{0}$

Obtenemos que la fuerza que la 1 produce sobre la 2 es no nula, pero la que la 2 produce sobre la 1 sí lo es, es decir, que no se cumple la 3ª ley de Newton.

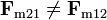
$\mathbf{F}_{\mathrm{m}21}\neq \mathbf{F}_{\mathrm{m}12}$

5.2 Empleando el campo magnético

6 Observaciones

Una observación más sobre esta fuerza magnética y su relación con la eléctrica. Al hablar del campo magnético producido por una carga puntual se introduce su velocidad, y en la fuerza de Lorentz aparece otra velocidad. la pregunta inmediata es ¿velocidad respecto a qué? No es la velocidad relativa de una carga respecto a la otra (ya que en este ejemplo, las dos cargas se mueven del mismo modo), sino la velocidad respecto a un sistema de referencia fijo. Ahora bien, una de las enseñanzas de la teoría de la relatividad es que no existen los sistemas de referencia absolutos. Si cambiamos de sistema de referencia absoluto resulta que la fuerza magnética valdrá más o menos o incluso anularse. Este comportamiento claramente no relativista de la fuerza magnética no puede ser correcto.

La expresión correcta de la fuerza electromagnética requiere meterse en las honduras de la relatividad especial, por lo que sólo indicaremos dos detalles:

Lo que tiene significado es la fuerza total, suma de la fuerza magnética y de la eléctrica

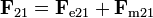
$\mathbf{F}_{21}=\mathbf{F}_{\mathrm{e}21}+\mathbf{F}_{\mathrm{m}21}$

La fuerza eléctrica también depende de la velocidad de las cargas (la ley de Coulomb es solo una aproximación), de forma que al cambiar de sistema de referencia no solo cambia la fuerza magnética, sino también la eléctrica (en una cantidad similar), de manera que la resultante sí se transforma como debe hacerlo una fuerza relativista.

@@ Línea 12: / Línea 12: @@
 [[Imagen:fuerzaBcargas.png|left|300px]] Podemos hallar la fuerza magnética entre las dos cargas empleando la [[Ley de Biot y Savart]] para cargas puntuales. La fuerza que la carga 1 produce sobre la 2 es
-<center><math>\mathbf{F}_{21} = \frac{\mu_0}{4\pi}\,\frac{q_1q_2\mathbf{v}_2\times(\mathbf{v}_1\times(\mathbf{r}_2-\mathbf{r}_1))}{|\mathbf{r}_2-\mathbf{r}_1|^3}</math></center>
+<center><math>\mathbf{F}_{\mathrm{m}21} = \frac{\mu_0}{4\pi}\,\frac{q_1q_2\mathbf{v}_2\times(\mathbf{v}_1\times(\mathbf{r}_2-\mathbf{r}_1))}{|\mathbf{r}_2-\mathbf{r}_1|^3}</math></center>
 donde en nuestro caso tenemos, tomando como Z el que pasa por la carga 1 y paralelo a su velocidad, y como eje X el que va de la carga 1 a la 2,
-<center>{{qquad}}{{qquad}}<math>\mathbf{r}_2-\mathbf{r}_1=a\mathbf{u}_x</math>{{qquad}}{{qquad}}<math>|\mathbf{r}_2-\mathbf{r}_1|=a</math>{{qquad}}{{qquad}}<math>\mathbf{v}_1=\mathbf{v}_2=v\mathbf{u}_z\,</math></center>
+<center><math>\mathbf{r}_2-\mathbf{r}_1=a\mathbf{u}_x</math>{{qquad}}{{qquad}}<math>|\mathbf{r}_2-\mathbf{r}_1|=a</math>{{qquad}}{{qquad}}<math>\mathbf{v}_1=\mathbf{v}_2=v\mathbf{u}_z\,</math></center>
 Sustituyendo nos queda
-<center><math>\mathbf{F}_{21}= \frac{\mu_0q_1q_2v^2}{4\pi a^2}\,\mathbf{u}_z\times(\mathbf{u}_z\times\mathbf{u}_x) = -\frac{\mu_0q_1q_2v^2}{4\pi a^2}\,\mathbf{u}_x</math></center>
+<center><math>\mathbf{F}_{\mathrm{m}21}= \frac{\mu_0q_1q_2v^2}{4\pi a^2}\,\mathbf{u}_z\times(\mathbf{u}_z\times\mathbf{u}_x) = -\frac{\mu_0q_1q_2v^2}{4\pi a^2}\,\mathbf{u}_x</math></center>
 donde hemos usado los [[Coordenadas_cartesianas._Base_vectorial#Base_ortonormal_dextrógira|productos entre los vectores de la base]]. Esta fuerza sobre la carga 2 va en la dirección de la 1, es decir, es atractiva.
@@ Línea 26: / Línea 26: @@
 Para hallar la fuerza que la carga 2 produce sobre la 1, lo único que cambia es que el vector de posición relativo es ahora <math>-a\mathbf{u}_x</math>, por lo que resulta una fuerza
-<center><math>\mathbf{F}_{12}=\frac{\mu_0q_1q_2v^2}{4\pi a^2}\,\mathbf{u}_x = -\mathbf{F}_{21}</math></center>
+<center><math>\mathbf{F}_{\mathrm{m}12}=\frac{\mu_0q_1q_2v^2}{4\pi a^2}\,\mathbf{u}_x = -\mathbf{F}_{21}</math></center>
 Esta fuerza es también atractiva, cumplie´ndose además la tercera ley de Newton.
@@ Línea 73: / Línea 73: @@
 ==Velocidades perpendiculares==
 ===Directamente===
+Aplicando de nuevo la expresión de la fuerza entre dos cargas en movimiento
+<center><math>\mathbf{F}_{\mathrm{m}21} = \frac{\mu_0}{4\pi}\,\frac{q_1q_2\mathbf{v}_2\times(\mathbf{v}_1\times(\mathbf{r}_2-\mathbf{r}_1))}{|\mathbf{r}_2-\mathbf{r}_1|^3}</math></center>
+donde tenemos ahora, al igual que antes
+<center><math>\mathbf{r}_2-\mathbf{r}_1=a\mathbf{u}_x</math>{{qquad}}{{qquad}}<math>|\mathbf{r}_2-\mathbf{r}_1|=a</math>{{qquad}}{{qquad}}<math>\mathbf{v}_1=v\mathbf{u}_z\,</math></center>
+siendo el único cambio
+<center><math>\mathbf{v}_2=v\mathbf{u}_x\,</math></center>
+que al sustituir nos da
+<center><math>\mathbf{F}_{\mathrm{m}21}= \frac{\mu_0q_1q_2v^2}{4\pi a^2}\,\mathbf{u}_x\times(\mathbf{u}_z\times\mathbf{u}_x) = \frac{\mu_0q_1q_2v^2}{4\pi a^2}\,\mathbf{u}_z</math></center>
+Si hallamos ahora la fuerza que la 2 produce sobre la 1
+<center><math>\mathbf{F}_{\mathrm{m}12}= \frac{\mu_0q_1q_2v^2}{4\pi a^2}\,\mathbf{u}_z\times(\mathbf{u}_x\times(-\mathbf{u}_x)) =\mathbf{0}</math></center>
+Obtenemos que la fuerza que la 1 produce sobre la 2 es no nula, pero la que la 2 produce sobre la 1 sí lo es, es decir, que ''no se cumple la 3ª ley de Newton''.
+<center><math>\mathbf{F}_{\mathrm{m}21}\neq \mathbf{F}_{\mathrm{m}12}</math></center>
 ===Empleando el campo magnético===

Fuerza entre dos cargas en movimiento

De Laplace

Revisión de 10:47 18 abr 2009

Contenido

1 Enunciado

2 Fuerza magnética

2.1 Directamente

2.2 Empleando el campo magnético

3 Comparación con la fuerza eléctrica

4 Cambio de signo

5 Velocidades perpendiculares

5.1 Directamente

5.2 Empleando el campo magnético

6 Observaciones

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES