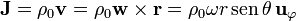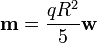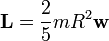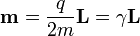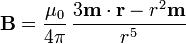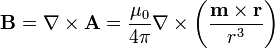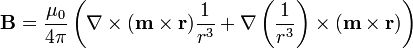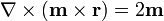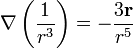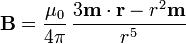|
|
| Línea 1: |
Línea 1: |
| - | ==Desarrollo multipolar magnético==
| |
| - | Supongamos que tenemos una distribución de corriente estacionaria que ocupa una pequeña región del espacio y queremos hallar el campo en puntos alejados.
| |
| - |
| |
| - | Cuando se dice “una pequeña región del espacio” se entiende que comparada con la distancia al punto de observación. Matemáticamente:
| |
| - |
| |
| - | <center><math>\delta=\frac{\mathrm{max}(|\mathbf{r}'|)}{r}\ll 1</math></center>
| |
| - |
| |
| - | Como con el [[Desarrollo multipolar eléctrico|campo eléctrico]], la idea del desarrollo multipolar es hacer un cálculo aproximado, más sencillo que la integral exacta (la cual puede ser imposible de calcular) mediante el empleo de una serie de Taylor. Partimos de la expresión del [[Potencial vector magnético|potencial vector]] para el caso de una espira
| |
| - |
| |
| - | <center><math>\mathbf{A}=\frac{\mu_0I}{4\pi}\oint\frac{\mathrm{d}\mathbf{r}'}{|\mathbf{r}-\mathbf{r}'|}</math></center>
| |
| - |
| |
| - | Aplicando el desarrollo del binomio de Newton
| |
| - |
| |
| - | <center><math>\frac{\mathrm{d}\mathbf{r}'}{|\mathbf{r}-\mathbf{r}'|}=\frac{1}{r}+\frac{\mathbf{r}\cdot\mathbf{r}'}{r^3}+\mathrm{O}(\delta^2)</math></center>
| |
| - |
| |
| - | resulta (de forma no trivial) la expresión aproximada para el potencial vector
| |
| - |
| |
| - | <center><math>\mathbf{A}=\frac{\mu_0}{4\pi}\frac{\mathbf{m}\times\mathbf{r}}{r^3}</math></center>
| |
| - |
| |
| - | donde
| |
| - |
| |
| - | <center><math>\mathbf{m}=\frac{I}{2}\oint \mathbf{r}'\times\mathrm{d}\mathbf{r}'</math></center>
| |
| - |
| |
| - | es el denominado ''momento magnético dipolar'' de la espira.
| |
| - |
| |
| - | A una distribución de corriente que produce este potencial vector (y el campo magnético resultante) se le denomina ''dipolo magnético''. Podemos imaginar un dipolo magnético como una pequeña espira de corriente, si bien el concepto es más general:
| |
| - |
| |
| - | * Una distribución de corriente de volumen confinada a una pequeña región del espacio también produce el campo de un dipolo magnético, siendo su momento dipolar
| |
| - |
| |
| - | <center><math>\mathbf{m}= \frac{1}{2}\int \mathbf{r}'\times\mathbf{J}\,\mathrm{d}\tau'</math></center>
| |
| - |
| |
| - | :En particular, este resultado incluye el caso de una distribución de carga en rotación.
| |
| - |
| |
| - | * Lo mismo ocurre para una distribución de corriente superficial
| |
| - |
| |
| - | <center><math>\mathbf{m}= \frac{1}{2}\int \mathbf{r}'\times\mathbf{K}\,\mathrm{d}S'</math></center>
| |
| - |
| |
| - | * La partículas elementales (electrones, protones,…) producen un campo magnético dipolar, en el que el momento magnético es proporcional al llamado espín de la partícula. Este momento dipolar no está asociado a ninguna corriente “clásica”, pero su comportamiento es análogo.
| |
| - |
| |
| - | ===Demostración detallada===
| |
| - | La obtención de la expresión aproximada del potencial vector no es elemental.
| |
| - |
| |
| - | Para empezar hay que justificar el desarrollo de <math>1/|\mathbf{r}-\mathbf{r}'|</math>. Para ello observamos que se puede escribir como
| |
| - |
| |
| - | <center><math>\frac{1}{|\mathbf{r}-\mathbf{r}'|}=\frac{1}{\sqrt{(\mathbf{r}-\mathbf{r}')\cdot(\mathbf{r}-\mathbf{r}')}}=\left(r^2-2\mathbf{r}\cdot\mathbf{r}'+r^{'2}\right)^{-1/2}</math></center>
| |
| - |
| |
| - | y sacando factor común un <math>r^2</math> de la raíz
| |
| - |
| |
| - | <center><math>\frac{1}{|\mathbf{r}-\mathbf{r}'|}=(r^2)^{-1/2}\left(1-2\frac{\mathbf{r}\cdot\mathbf{r}'}{r^2}+\frac{r^{'2}}{r^2}\right)^{-1/2} = \frac{1}{r}\left(1+\left(-2\frac{\mathbf{r}\cdot\mathbf{r}'}{r^2}+\frac{r^{'2}}{r^2}\right)\right)^{-1/2}</math></center>
| |
| - |
| |
| - | Hasta aquí no hay aproximación alguna. Observamos que en el último factor tenemos 1 más algo mucho más pequeño que la unidad (pues <math>r'\ll r</math>). La fórmula general del binomio de Newton nos dice que si <math>x\ll 1</math>
| |
| - |
| |
| - | <center><math>(1+x)^n = 1 + n x + \mathrm{O}(x^2)\,</math></center>
| |
| - |
| |
| - | Aplicando esto al resultado anterior
| |
| - |
| |
| - | <center><math>\frac{1}{|\mathbf{r}-\mathbf{r}'|} = \frac{1}{r}\left(1+\left(-2\frac{\mathbf{r}\cdot\mathbf{r}'}{r^2}+\frac{r^{'2}}{r^2}\right)\right)^{-1/2} = \frac{1}{r}\left(1-\frac{1}{2}\left(-2\frac{\mathbf{r}\cdot\mathbf{r}'}{r^2}+\frac{r^{'2}}{r^2}\right)+\mathrm{O}(\delta^2)\right)</math></center>
| |
| - |
| |
| - | pero de hecho, el segundo de los dos sumandos del paréntesis también es de orden <math>\delta^2</math>, por lo que podemos despreciarlo y reducir el desarrollo a
| |
| - |
| |
| - | <center><math>\frac{1}{|\mathbf{r}-\mathbf{r}'|} = \frac{1}{r}\left(1+\frac{\mathbf{r}\cdot\mathbf{r}'}{r^2}+\mathrm{O}(\delta^2)\right)=
| |
| - | \frac{1}{r}+\frac{\mathbf{r}\cdot\mathbf{r}'}{r^3}+\cdots</math></center>
| |
| - |
| |
| - | El segundo paso es sustituir esto en la expresión del potencial vector. Nos queda
| |
| - |
| |
| - | <center><math>\mathbf{A}=\frac{\mu_0I}{4\pi}\left(\oint\frac{\mathrm{d}\mathbf{r}'}{r}+\oint\frac{(\mathbf{r}\cdot\mathrm{r}')\mathrm{d}\mathbf{r}'}{r^3}+\cdots\right)</math></center>
| |
| - |
| |
| - | Estas integrales son sobre la variable <math>\mathbf{r}'</math>, así que <math>\mathbf{r}</math> es una constante en ellas y puede ser extraído en la medida de lo posible
| |
| - |
| |
| - | <center><math>\mathbf{A}=\frac{\mu_0I}{4\pi}\left(\frac{1}{r}\oint\mathrm{d}\mathbf{r}'+\frac{1}{r^3}\oint(\mathbf{r}\cdot\mathrm{r}')\mathrm{d}\mathbf{r}'+\cdots\right)</math></center>
| |
| - |
| |
| - | La primera de estas dos integrales es el desplazamiento neto al recorrer una curva cerrada, por lo que se anula identicamente,
| |
| - |
| |
| - | <center><math>\oint \mathrm{d}\mathbf{r}'=\left.\mathbf{r}'\right|_{\mathbf{r}_0}^{\mathbf{r}_0}=\mathbf{0}</math></center>
| |
| - |
| |
| - | Lo que nos dice este resultado, de nuevo, es que el campo magnético de corrientes estacionarias, no posee término monopolar, esto es, que el campo de corrientes no equivale al campo de cargas magnéticas (''[[monopolo magnético|monopolos]]'').
| |
| - |
| |
| - | El segundo término no se puede integrar de forma inmediata. Para conseguir extraer <math>\mathbf{r}</math> de la integral podemos usar el [[Generalización del teorema de Stokes|teorema vectorial]], generalización del teorema de Stokes
| |
| - |
| |
| - | <center><math>\oint \mathrm{d}\mathbf{r}' \phi = \int \mathrm{d}\mathbf{S}\times\nabla\phi</math></center>
| |
| - |
| |
| - | que, en nuestro caso da
| |
| - |
| |
| - | <center><math>\oint \mathrm{d}\mathbf{r}'(\mathbf{r}\cdot\mathrm{r}') = \int \mathrm{d}\mathbf{S}\times\nabla'(\mathbf{r}\cdot\mathrm{r}')</math></center>
| |
| - |
| |
| - | pero, como se [[Algunas identidades vectoriales|puede demostrar]]
| |
| - |
| |
| - | <center><math>\nabla'(\mathbf{r}\cdot\mathbf{r}')=\mathbf{r}</math></center>
| |
| - |
| |
| - | por lo que la integral se convierte en
| |
| - |
| |
| - | <center><math>\oint \mathrm{d}\mathbf{r}'(\mathbf{r}\cdot\mathrm{r}') = \int \mathrm{d}\mathbf{S}\times\mathbf{r}=\mathbf{S}\times\mathbf{r}</math></center>
| |
| - |
| |
| - | y, aplicación la expresión del [[vector superficie]]
| |
| - |
| |
| - | <center><math>\mathbf{S}=\frac{1}{2}\oint \mathbf{r}'\times \mathrm{d}\mathbf{r}'</math></center>
| |
| - |
| |
| - | nos queda finalmente
| |
| - |
| |
| - | <center><math>\mathbf{A}=\frac{\mu_0}{4\pi}\,\frac{\mathrm{m}\times\mathbf{r}}{r^3}+\cdots</math>{{qquad}}{{qquad}}<math>\mathbf{m}=I\mathbf{S}=\frac{I}{2}\oint \mathbf{r}'\times \mathrm{d}\mathbf{r}'</math></center>
| |
| - |
| |
| - | La extensión al caso de una distribución de corriente volumétrica o superficial requiere aun más cálculo vectorial, por lo que nos limitaremos a señalar que puede obtenerse siguiento las reglas usuales de transformación
| |
| - |
| |
| - | <center><math>\int_\Gamma(\ldots)I\mathrm{d}\mathbf{r}'\to \int_S(\ldots)\mathbf{K}\mathrm{d}S'\to\int_\tau(\ldots)\mathbf{J}\mathrm{d}\tau'</math></center>
| |
| - |
| |
| | ==Momento dipolar magnético== | | ==Momento dipolar magnético== |
| | ===Para una espira=== | | ===Para una espira=== |
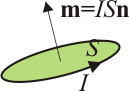
El momento magnético dipolar de una espira cerrada por la cual circula una corriente I viene dado por la expresión
De las expresiones anteriores, es evidente que la unidad del momento magnético en el Sistema Internacional es 1 A·m².
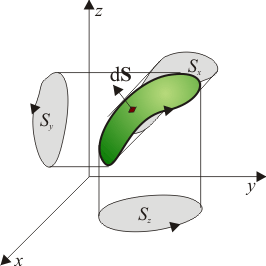
El momento dipolar puede también calcularse, además de para una corriente lineal, para una distribución de corriente superficial, una de volumen, o una superposición de ellas. Las expresiones correspondientes son
Un caso particular de corriente de volumen localizada en el espacio es el de una distribución de carga en rotación. Este modelo puede ayudar a describir el comportamiento de una partícula cargada, como un electrón, que se caracteriza por un momento angular (el espín), equivalente en ciertos aspectos a una rotación.
Lo más destacado de este resultado es que es proporcional a la velocidad angular de la partícula. Puesto que lo mismo ocurre con el momento angular
puede establecerse una relación de proporcionalidad entre el momento magnético y el momento angular
El campo magnético debido a un dipolo se halla tomando el rotacional del potencial vector. El resultado es
Desarrollando el doble producto vectorial se llega finalmente a la expresión del campo magnético.
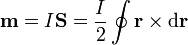
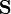 es el vector superficie, por lo que
es el vector superficie, por lo que
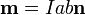
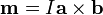
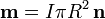
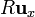 a
a 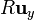 , de ahí a
, de ahí a 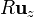 , y de vuelta a
, y de vuelta a 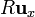 . Tal como se ve en artículo sobre el vector superficie, para esta superficie tenemos
. Tal como se ve en artículo sobre el vector superficie, para esta superficie tenemos
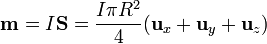
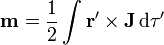
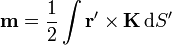
 . Para este sistema la densidad de corriente es, en esféricas
. Para este sistema la densidad de corriente es, en esféricas