Campo magnético debido a una magnetización

De Laplace

(Diferencias entre revisiones)

última version al 13:07 2 abr 2009

Contenido

1 Potencial vector
- 1.1 Demostración
2 Campo magnético
3 Ejemplo: imán esférico
4 Comparación con el caso dieléctrico

1 Potencial vector

El potencial vector magnético debido a una magnetización es una extensión de la expresión correspondiente a un solo dipolo

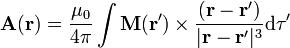
$\mathbf{A}(\mathbf{r})=\frac{\mu_0}{4\pi}\int \mathbf{M}(\mathbf{r}')\times\frac{(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}\mathrm{d}\tau'$

1.1 Demostración

La demostración es una consecuencia inmediata del principio de superposición. El potencial vector debido a un dipolo situado en el origen de coordenadas es

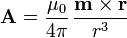
$\mathbf{A}=\frac{\mu_0}{4\pi}\,\frac{\mathbf{m}\times\mathbf{r}}{r^3}$

Si el dipolo no está en el origen, sino en el punto $\mathbf{r}_0$ , se efectúa una traslación

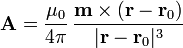
$\mathbf{A}=\frac{\mu_0}{4\pi}\,\frac{\mathbf{m}\times(\mathbf{r}-\mathbf{r}_0)}{|\mathbf{r}-\mathbf{r}_0|^3}$

Si tenemos N dipolos, superponemos los potenciales respectivos

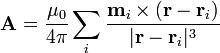
$\mathbf{A}=\frac{\mu_0}{4\pi}\sum_i\frac{\mathbf{m}_i\times(\mathbf{r}-\mathbf{r}_i)}{|\mathbf{r}-\mathbf{r}_i|^3}$

Para pasar a una distribución continua, organizamos el sumatorio, de forma que primero sumamos todos los dipolos que están dentro de un elemento y luego sumamos para todos los elementos

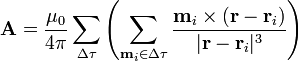
$\mathbf{A}=\frac{\mu_0}{4\pi}\sum_{\Delta\tau}\left(\sum_{\mathbf{m}_i\in\Delta\tau}\frac{\mathbf{m}_i\times(\mathbf{r}-\mathbf{r}_i)}{|\mathbf{r}-\mathbf{r}_i|^3}\right)$

Hasta aquí no hay aproximación alguna. Dado que los elementos de volumen son microscópicos, podemos suponer que todos los dipolos de cada elemento se encuentran en la misma posición 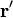$\mathbf{r}'$

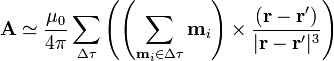
$\mathbf{A}\simeq\frac{\mu_0}{4\pi}\sum_{\Delta\tau}\left(\left(\sum_{\mathbf{m}_i\in\Delta\tau}\mathbf{m}_i\right)\times\frac{(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}\right)$

y, por la definición de magnetización

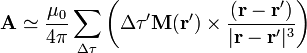
$\mathbf{A}\simeq\frac{\mu_0}{4\pi}\sum_{\Delta\tau}\left(\Delta\tau'\mathbf{M}(\mathbf{r}')\times\frac{(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}\right)$

En el límite, este sumatorio se convierte en una integral

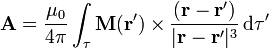
$\mathbf{A}=\frac{\mu_0}{4\pi}\int_\tau\mathbf{M}(\mathbf{r}')\times\frac{(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}\,\mathrm{d}\tau'$

2 Campo magnético

Una vez que se tiene el potencial vector, puede hallarse el campo magnético

$\mathbf{B}=\nabla\times\mathbf{A}$

También puede calcularse a partir de la superposición del campo de dipolos magnéticos

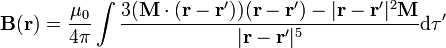
$\mathbf{B}(\mathbf{r})=\frac{\mu_0}{4\pi}\int \frac{3(\mathbf{M}\cdot(\mathbf{r}-\mathbf{r}'))(\mathbf{r}-\mathbf{r}')-|\mathbf{r}-\mathbf{r}'|^2\mathbf{M}}{|\mathbf{r}-\mathbf{r}'|^5}\mathrm{d}\tau'$

No obstante, la complejidad de estas integrales aconseja el uso de métodos alternativos de cálculo.

3 Ejemplo: imán esférico

Artículo completo: Imán esférico

Uno de los pocos casos que admiten integración directa es el imán esférico (ya estudiado por [Pierre de Maricourt] en el siglo XIII) y que describe tanto el campo magnético terrestre, como el comportamiento de una partícula esférica (por ejemplo, una limadura de hierro) en el seno de un campo magnético.

Para este sistema, la integración del potencial vector da

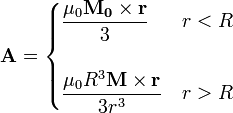
$\mathbf{A}=\begin{cases}\displaystyle\frac{\mu_0\mathbf{M_0}\times\mathbf{r}}{3} & r<R \\ & \\ \displaystyle\frac{\mu_0R^3\mathbf{M}\times\mathbf{r}}{3r^3} & r>R\end{cases}$

y de aquí se obtiene un campo magnético en el interior de la esfera ( $r < R$ )

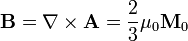
$\mathbf{B}=\nabla\times\mathbf{A}= \frac{2}{3}\mu_0\mathbf{M}_0$

esto es, un campo uniforme en la misma dirección y sentido que la imanación.

En el exterior de la esfera ( $r > R$ ) el campo equivale al de un dipolo magnético situado en el centro

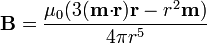
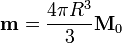
$\mathbf{B}=\frac{\mu_0(3(\mathbf{m}{\cdot}\mathbf{r})\mathbf{r}-r^2\mathbf{m})}{4\pi r^5}$ $\mathbf{m}=\frac{4\pi R^3}{3}\mathbf{M}_0$

4 Comparación con el caso dieléctrico

Existe un paralelismo entre el potencial vector de una magnetización y el potencial eléctrico de una polarización:

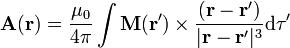
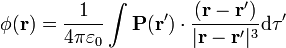
$\mathbf{A}(\mathbf{r})=\frac{\mu_0}{4\pi}\int \mathbf{M}(\mathbf{r}')\times\frac{(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}\mathrm{d}\tau'$ $\phi(\mathbf{r})=\frac{1}{4\pi\varepsilon_0}\int \mathbf{P}(\mathbf{r}')\cdot\frac{(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}\mathrm{d}\tau'$

Vemos que, además de aparecer la constante correspondiente, la única diferencia es el tipo de producto: vectorial para el potencial vector y escalar para el potencial escalar.

@@ Línea 46: / Línea 46: @@
 ==Ejemplo: imán esférico==
 {{ac|Imán esférico}}
-Uno de los pocos casos que admiten integración directa es el imán esférico (ya estudiado por Pierre de Maricourt en el siglo XIII) y que describe tanto el campo magnético terrestre, como el comportamiento de una partícula esférica (por ejemplo, una limadura de hierro) en el seno de un campo magnético.
+Uno de los pocos casos que admiten integración directa es el imán esférico (ya estudiado por [[http://en.wikipedia.org/wiki/Petrus_Peregrinus Pierre de Maricourt]] en el siglo XIII) y que describe tanto el campo magnético terrestre, como el comportamiento de una partícula esférica (por ejemplo, una limadura de hierro) en el seno de un campo magnético.
-Para este sistema, la integración del potencial vector es
+Para este sistema, la integración del potencial vector da
 <center><math>\mathbf{A}=\begin{cases}\displaystyle\frac{\mu_0\mathbf{M_0}\times\mathbf{r}}{3} & r<R \\ & \\ \displaystyle\frac{\mu_0R^3\mathbf{M}\times\mathbf{r}}{3r^3} &  r>R\end{cases}</math></center>
+y de aquí se obtiene un campo magnético en el interior de la esfera (<math>r<R</math>)
+<center><math>\mathbf{B}=\nabla\times\mathbf{A}= \frac{2}{3}\mu_0\mathbf{M}_0</math></center>
+esto es, un campo uniforme en la misma dirección y sentido que la imanación.
+En el exterior de la esfera (<math>r>R</math>) el campo equivale al de un dipolo magnético situado en el centro
+<center><math>\mathbf{B}=\frac{\mu_0(3(\mathbf{m}{\cdot}\mathbf{r})\mathbf{r}-r^2\mathbf{m})}{4\pi r^5}</math>{{qquad}}{{qquad}}<math>\mathbf{m}=\frac{4\pi R^3}{3}\mathbf{M}_0</math></center>
+==Comparación con el caso dieléctrico==
+Existe un paralelismo entre el potencial vector de una magnetización y el potencial eléctrico de una [[polarización]]:
+<center><math>\mathbf{A}(\mathbf{r})=\frac{\mu_0}{4\pi}\int \mathbf{M}(\mathbf{r}')\times\frac{(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}\mathrm{d}\tau'</math>{{qquad}}{{qquad}}<math>\phi(\mathbf{r})=\frac{1}{4\pi\varepsilon_0}\int \mathbf{P}(\mathbf{r}')\cdot\frac{(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}\mathrm{d}\tau'</math></center>
+Vemos que, además de aparecer la constante correspondiente, la única diferencia es el tipo de producto: vectorial para el potencial vector y escalar para el potencial escalar.
 [[Categoría:Materiales magnéticos]]

Campo magnético debido a una magnetización

De Laplace

última version al 13:07 2 abr 2009

Contenido

1 Potencial vector

1.1 Demostración

2 Campo magnético

3 Ejemplo: imán esférico

4 Comparación con el caso dieléctrico

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES