Campo magnético debido a una magnetización
De Laplace
(Diferencias entre revisiones)
(→Demostración) |
|||
| Línea 7: | Línea 7: | ||
La demostración es una consecuencia inmediata del principio de superposición. El potencial vector debido a un [[dipolo magnético|dipolo situado en el origen de coordenadas]] es | La demostración es una consecuencia inmediata del principio de superposición. El potencial vector debido a un [[dipolo magnético|dipolo situado en el origen de coordenadas]] es | ||
| - | <center><math>\mathbf{A}=\frac{\mu_0}{4\pi}\,\frac{\mathbf{m}\times\mathbf{r}}{r^3</math></center> | + | <center><math>\mathbf{A}=\frac{\mu_0}{4\pi}\,\frac{\mathbf{m}\times\mathbf{r}}{r^3}</math></center> |
| - | + | ||
==Campo magnético== | ==Campo magnético== | ||
Revisión de 20:08 1 abr 2009
Contenido |
1 Potencial vector
El potencial vector magnético debido a una magnetización es una extensión de la expresión correspondiente a un solo dipolo
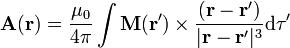
1.1 Demostración
La demostración es una consecuencia inmediata del principio de superposición. El potencial vector debido a un dipolo situado en el origen de coordenadas es
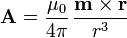
2 Campo magnético
Una vez que se tiene el potencial vector, puede hallarse el campo magnético

También puede calcularse a partir de la superposición del campo de dipolos magnéticos
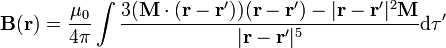
No obstante, la complejidad de estas integrales aconseja el uso de métodos alternativos de cálculo.
3 Ejemplo: imán esférico
Artículo completo: Imán esférico





