Flujo de líquido por una tubería
De Laplace
(→Intensidad de corriente) |
|||
| (3 ediciones intermedias no se muestran.) | |||
| Línea 9: | Línea 9: | ||
# Si se desea que por la superficie del tubo circule una corriente superficial <math>\mathbf{K}</math>, de forma que la corriente total sea nula, ¿cuánto debe valer <math>\mathbf{K}</math>? | # Si se desea que por la superficie del tubo circule una corriente superficial <math>\mathbf{K}</math>, de forma que la corriente total sea nula, ¿cuánto debe valer <math>\mathbf{K}</math>? | ||
| - | + | ==Intensidad de corriente== | |
| - | + | ||
La intensidad de corriente es igual al flujo de la densidad de corriente a través de una superficie abierta atravesada por ésta. En este sistema la superficie más adecuada es una sección circular de la tubería, perpendicular a su eje. | La intensidad de corriente es igual al flujo de la densidad de corriente a través de una superficie abierta atravesada por ésta. En este sistema la superficie más adecuada es una sección circular de la tubería, perpendicular a su eje. | ||
En coordenadas cilíndricas esta superficie es <math>z = z_0 = \mathrm{cte}</math>, lo que nos da la intensidad | En coordenadas cilíndricas esta superficie es <math>z = z_0 = \mathrm{cte}</math>, lo que nos da la intensidad | ||
| - | <center><math>I = \int_S \mathbf{J}\cdot\mathrm{d}\mathbf{S} = \int_0^{2\pi}\int_0^a | + | <center><math>I = \int_S \mathbf{J}\cdot\mathrm{d}\mathbf{S} = \int_0^{2\pi}\int_0^a \left(v_0\left(1-\frac{\rho^2}{a^2}\right)\mathbf{u}_{z}\right)\cdot\left(\rho\,\mathrm{d}\rho\,\mathrm{d}\varphi\,\mathbf{u}_z\right)</math></center> |
El producto escalar vale la unidad, pues la corriente y el vector normal a la superficie son vectores paralelos. La integral en <math>\varphi</math> nos da un factor <math>2\pi</math>, mientras que la integral en <math>\rho</math> es una polinómica. La corriente vale entonces | El producto escalar vale la unidad, pues la corriente y el vector normal a la superficie son vectores paralelos. La integral en <math>\varphi</math> nos da un factor <math>2\pi</math>, mientras que la integral en <math>\rho</math> es una polinómica. La corriente vale entonces | ||
| Línea 21: | Línea 20: | ||
<center><math>I = 2\pi\rho_0v_0 \int_0^a \left(\rho-\frac{\rho^3}{a^2}\right)\,\mathrm{d}\rho = \frac{\pi\rho_0v_0a^2}{2}</math></center> | <center><math>I = 2\pi\rho_0v_0 \int_0^a \left(\rho-\frac{\rho^3}{a^2}\right)\,\mathrm{d}\rho = \frac{\pi\rho_0v_0a^2}{2}</math></center> | ||
| - | + | ==Corriente superficial== | |
| + | Si existe una corriente de retorno uniforme | ||
| + | |||
| + | <center><math>\mathbf{K}=K_0\mathbf{u}_z\,</math></center> | ||
| + | |||
| + | sobre la superficie del tubo, la intensidad de corriente asociada a esta densidad es | ||
| + | |||
| + | <center><math>I_1 = \int_\Gamma \mathbf{K}\cdot\mathbf{n}_1\,\mathrm{d}l</math></center> | ||
| + | |||
| + | siendo <math>\Gamma</math> una curva atravesada por la corriente superficial y <math>\mathbf{n}_1</math> un vector unitario normal a la curva <math>\Gamma</math> y tangente a la superficie por la que fluye la corriente. En nuestro caso lo más simple es tomar <math>\Gamma</math> como una circunferencia que corta al tubo (el borde del círculo que hemos considerado antes con la corriente de volumen). | ||
| + | Para esta curva | ||
| + | |||
| + | <center><math>\mathrm{d}l = \rho\,\mathrm{d}\varphi=a\,\mathrm{d}\varphi</math>{{qquad}}{{qquad}}<math>\mathbf{n}_1=\mathbf{u}_z\, | ||
| + | </math></center> | ||
| + | |||
| + | y nos queda una intensidad de corriente sobre la superficie | ||
| + | |||
| + | <center><math>I_1 = \int_0^{2\pi}\left(K_0\,\mathbf{u}_z\right)\cdot\left(\mathbf{u}_z\,a\,\mathrm{d}\varphi\right) = 2\pi a K_0</math></center> | ||
| + | |||
| + | Si esta corriente debe cancelar la que fluye por el interior de la tubería, su valor debe ser | ||
| + | |||
| + | <center> | ||
| + | <math>I_1 = -I\,</math>{{tose}}<math>2\pi a K_0 = -\frac{\pi\rho_0v_0a^2}{2}</math>{{tose}}<math>\mathbf{K} = -\frac{\rho_0v_0a}{4}\,\mathbf{u}_z</math></center> | ||
| + | |||
| + | Esta corriente, por supuesto, fluye en sentido opuesto a la que va el interior de la tubería. | ||
| + | |||
[[Categoría:Problemas de corriente eléctrica]] | [[Categoría:Problemas de corriente eléctrica]] | ||
última version al 20:23 31 mar 2009
1 Enunciado
Por el interior de una tubería cilíndrica de radio a fluye un líquido con una velocidad, dependiente de la distancia al eje, ρ, como
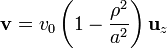
El líquido posee una densidad de carga uniforme ρ0, de forma que la densidad de corriente es 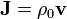 . En el exterior del tubo no hay corriente.
. En el exterior del tubo no hay corriente.
- Calcule la intensidad de corriente que atraviesa una sección por la tubería.
- Si se desea que por la superficie del tubo circule una corriente superficial
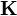 , de forma que la corriente total sea nula, ¿cuánto debe valer
, de forma que la corriente total sea nula, ¿cuánto debe valer 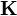 ?
?
2 Intensidad de corriente
La intensidad de corriente es igual al flujo de la densidad de corriente a través de una superficie abierta atravesada por ésta. En este sistema la superficie más adecuada es una sección circular de la tubería, perpendicular a su eje.
En coordenadas cilíndricas esta superficie es z = z0 = cte, lo que nos da la intensidad
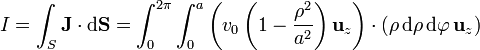
El producto escalar vale la unidad, pues la corriente y el vector normal a la superficie son vectores paralelos. La integral en  nos da un factor 2π, mientras que la integral en ρ es una polinómica. La corriente vale entonces
nos da un factor 2π, mientras que la integral en ρ es una polinómica. La corriente vale entonces

3 Corriente superficial
Si existe una corriente de retorno uniforme
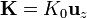
sobre la superficie del tubo, la intensidad de corriente asociada a esta densidad es
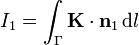
siendo Γ una curva atravesada por la corriente superficial y 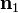 un vector unitario normal a la curva Γ y tangente a la superficie por la que fluye la corriente. En nuestro caso lo más simple es tomar Γ como una circunferencia que corta al tubo (el borde del círculo que hemos considerado antes con la corriente de volumen).
Para esta curva
un vector unitario normal a la curva Γ y tangente a la superficie por la que fluye la corriente. En nuestro caso lo más simple es tomar Γ como una circunferencia que corta al tubo (el borde del círculo que hemos considerado antes con la corriente de volumen).
Para esta curva
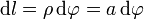
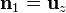
y nos queda una intensidad de corriente sobre la superficie
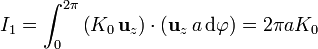
Si esta corriente debe cancelar la que fluye por el interior de la tubería, su valor debe ser
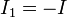

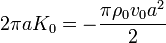

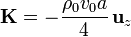
Esta corriente, por supuesto, fluye en sentido opuesto a la que va el interior de la tubería.





