Imán esférico
De Laplace
(Diferencias entre revisiones)
(Nueva página: ==Enunciado== Se dispone de una esfera de radio <math>R</math> con una imanación permanente <math>\mathbf{M}=M_0\mathbf{u}_{z}</math>. # Determine la expresión integral del potenci...) |
(→Enunciado) |
||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| - | Se dispone de una esfera de radio <math>R</math> con una imanación permanente <math>\mathbf{M}=M_0\mathbf{u}_{z}</math>. | + | {{nivel|3}}Se dispone de una esfera de radio <math>R</math> con una imanación permanente <math>\mathbf{M}=M_0\mathbf{u}_{z}</math>. |
# Determine la expresión integral del potencial vector magnético. Calcule el valor de la integral. Hállese, a partir de <math>\mathbf{A}</math>, el valor de <math>\mathbf{B}</math> y de <math>\mathbf{H}</math> en todos los puntos del espacio. | # Determine la expresión integral del potencial vector magnético. Calcule el valor de la integral. Hállese, a partir de <math>\mathbf{A}</math>, el valor de <math>\mathbf{B}</math> y de <math>\mathbf{H}</math> en todos los puntos del espacio. | ||
Revisión de 12:18 30 mar 2009
Contenido |
1 Enunciado
Se dispone de una esfera de radio R con una imanación permanente 
.
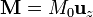- Determine la expresión integral del potencial vector magnético. Calcule el valor de la integral. Hállese, a partir de
, el valor de 
y de 
en todos los puntos del espacio.
- Describa cualitativamente la forma de , y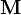
- Calcule las corrientes de magnetización equivalentes, las ecuaciones y las condiciones de contorno para .
- Halle la distribución de cargas magnéticas equivalentes y el problema de ecuaciones y condiciones de contorno para .
