Cómo se hace una integral
De Laplace
(Diferencias entre revisiones)
(→Idea general) |
(→Una integral de camino) |
||
| Línea 9: | Línea 9: | ||
==Una integral de camino== | ==Una integral de camino== | ||
| + | |||
| + | Por poner un ejemplo, supongamos que nos piden, dado el campo | ||
| + | |||
| + | <center><math>\mathbf{A} = (x-y)\mathbf{u}_x+(x+y)\mathbf{u}_y + z\mathbf{z}</math></center> | ||
===Parametrización=== | ===Parametrización=== | ||
Revisión de 11:46 23 nov 2007
Contenido |
1 Idea general
A la hora de enfrentarse a una integral (de camino, superficie o volumen, escalar o vectorial) hay que distinguir dos tareas: plantearla y calcularla. Es importante distinguir estas dos fases, porque si se intenta hacer todo de golpe la tarea puede parecer insuperable.
- La fase de planteamiento es la más importante. Dada una cierta expresión integral (o quizás simplemente una idea de que hay que sumar algo) hay que reducirla a una o varias integrales elementales, cada una de las cuales se puede resolver (o no) empleando las técnicas aprendidas en Cálculo.
- La forma de hacer esto es sencilla: basta con seguir al pie de la letra lo que pone en la expresión integral, respectando qué es un vector, qué es un escalar, qué tipos de productos aparecen o qué tipos de diferenciales hay que usar.
- La fase de cálculo consiste en, una vez reducida la expresión vectorial a una o varias integrales elementales, hallar el valor de cada una. En este paso lo más importante es tener cuidado con cuál variable es de integración y cuál funciona como constante.
2 Una integral de camino
Por poner un ejemplo, supongamos que nos piden, dado el campo
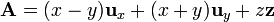
2.1 Parametrización
3 Dos integrales de superficie
4 Enlaces
- Siguiente:
- Anterior: Coordenadas esféricas. Diferenciales





