Ley de Lorentz
De Laplace
(→Demostración) |
(→Fuerza sobre una corriente lineal) |
||
| Línea 122: | Línea 122: | ||
==Fuerza sobre una corriente lineal== | ==Fuerza sobre una corriente lineal== | ||
| - | El caso importante de la fuerza sobre una corriente filiforme puede deducirse de la expresión para una distribución volumétrica. El resultado es que si tenemos una corriente I circulando a lo largo de una curva | + | El caso importante de la fuerza sobre una corriente filiforme puede deducirse de la expresión para una distribución volumétrica. El resultado es que si tenemos una corriente <math>I</math> circulando a lo largo de una curva <math>\Gamma</math> (abierta o cerrada) la fuerza magnética sobre la corriente es<center> |
<math>\mathbf{F}_\mathrm{m}=I\int_\Gamma \mathrm{d}\mathbf{r}\times\mathbf{B}</math></center> | <math>\mathbf{F}_\mathrm{m}=I\int_\Gamma \mathrm{d}\mathbf{r}\times\mathbf{B}</math></center> | ||
Revisión de 16:29 18 mar 2009
Contenido |
1 Fuerza sobre cargas puntuales
1.1 Ley de Lorentz
Según se ve en el tema de Electrostática en el vacío, la fuerza eléctrica sobre una carga puntual en reposo viene dada por
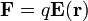
Sin embargo, si dicha carga se encuentra en movimiento, la experiencia muestra que se ve sometida a una fuerza adicional. Esta fuerza, que llamaremos fuerza magnética, verifica que es:
- Proporcional a la carga
- Proporcional al módulo de su velocidad
- Perpendicular a la velocidad
Con estas condiciones, la fuerza magnética debe ser de la forma
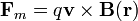
siendo  un nuevo campo, conocido como campo magnético. La fuerza total sobre una carga puntual es entonces
un nuevo campo, conocido como campo magnético. La fuerza total sobre una carga puntual es entonces
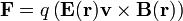
Esta expresión, que es válida en general, tanto para situaciones estáticas como dinámicas, se denomina Fuerza de Lorentz.
1.2 Unidades del campo magnético
De la expresión de la fuerza magnética resulta que, en el SI,  se mide en
se mide en
![[B] = \frac{{[F]}}{{[q][v]}} = \frac{{\left( {1\,{\rm{N}}} \right)}}{{\left( {1{\rm{C}}} \right)\,\left( {1{\rm{m}}/{\rm{s}}} \right)}} = \frac{{1\,{\rm{N}}}}{{{\rm{A}}\cdot{\rm{m}}}} = 1\,{\rm{T}}](/wiki/images/math/a/6/b/a6be200933d8f4311d64db81939b0c70.png)
A esta unidad se la denomina Tesla, en honor del científico e ingeniero Nikola Tesla.
1.3 ¿Y los imanes?
El concepto de campo magnético suele asociarse sobre todo con los imanes. Sin embargo, las experiencias de Øersted de 1820 mostraron que: Las corrientes eléctricas producen fuerzas magnéticas sobre los imanes.
A partir de ahí, Ampère por un lado y Biot y Savart por otro, postularon la expresión simétrica:
Los imanes producen fuerzas magnéticas sobre las corrientes eléctricas
Y por tanto
Las corrientes eléctricas producen fuerzas magnéticas entre sí
Ampère postuló además que también las fuerzas magnéticas entre imanes son interacciones entre corrientes. Puesto que las corrientes eléctricas no son más que conjuntos de cargas en movimiento:
El magnetismo se reduce a la interacción entre cargas
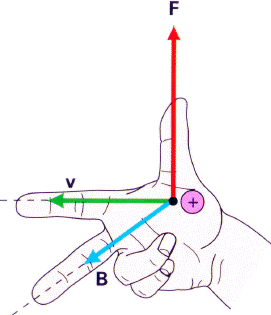
1.4 La regla de la mano derecha
Es indispensable al estudiar el campo magnético: Si el índice apunta según v y el corazón según B, el pulgar indica la fuerza.
2 Movimiento de una carga en un campo magnético
¿Cómo se conocen las propiedades de la fuerza magnética indicadas anteriormente? Una posibilidad es estudiando el movimiento de una carga en un campo uniforme.
Supongamos un campo magnético 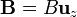 , y una carga q que penetra en el campo con velocidad inicial v0. Tenemos tres casos:
, y una carga q que penetra en el campo con velocidad inicial v0. Tenemos tres casos:
2.1 Velocidad inicial paralela
En este caso la fuerza inicial es nula
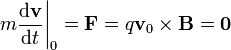
La velocidad no cambia ni entonces ni más tarde, por lo que el movimiento es rectilíneo y uniforme paralelo a B
2.2 Velocidad inicial perpendicular
Como la fuerza es perpendicular a  , se cumple que
, se cumple que 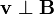 en todo instante.
en todo instante.
Escribiendo la 2ª ley de Newton en componentes intrínsecas
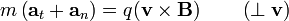
La fuerza es puramente normal a  , por lo que la aceleración tangencial es nula
, por lo que la aceleración tangencial es nula


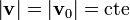
y, al ser la celeridad constante
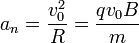

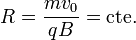
Resultan una celeridad y un radio de curvatura constantes, por tanto el movimiento es circular y uniforme alrededor del campo magnético.

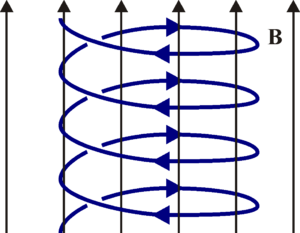
2.3 Velocidad inicial arbitraria
Descomponiendo el movimiento en los dos casos anteriores, resulta una superposición de un movimiento circular alrededor del campo, combinado con uno rectilíneo paralelo a éste.
El resultado es un movimiento helicoidal uniforme
3 Fuerza sobre una distribución de corriente
Normalmente las cargas eléctricas no están aisladas, sino agrupadas por millones formando una distribución de corriente. La fuerza neta sobre la distribución será la resultante de las fuerzas individuales

Como en otras ocasiones, no resulta factible hallar la fuerza mediante el sumatorio, ya que para empezar desconocemos la posición y la velocidad de cada partícula, ni siquiera sabemos cuántas hay. Por ello, es necesario pasar a una descripción macroscópica. Supongamos que tenemos un volumen τ, en el interior del cual hay una distribución de corriente de volumen J. La fuerza neta sobre la distribución es
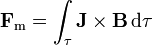
El mismo razonamiento que para una distribución volumétrica se puede aplicar a una superficial, resultando la fuerza

3.1 Demostración
En lugar de sumar las cargas en cualquier orden, dividimos el volumen en elementos Δτ, y sumamos primero dentro de cada elemento
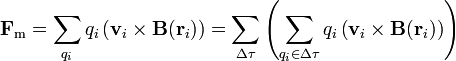
Hacemos la aproximación de que, dentro de un elemento, todas las cargas ven el mismo campo promedio y se puede sacar como factor común

El sumatorio de las cargas por las velocidades equivale a la densidad de corriente por el elemento de volumen
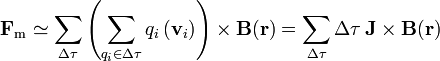
Y, considerando los elementos como de tamaño diferencial, resulta finalmente la integral
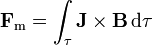
Aunque en el proceso hemos realizado algunas aproximaciones, en el límite 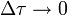 se convierten en identidades.
se convierten en identidades.
4 Fuerza sobre una corriente lineal
El caso importante de la fuerza sobre una corriente filiforme puede deducirse de la expresión para una distribución volumétrica. El resultado es que si tenemos una corriente I circulando a lo largo de una curva Γ (abierta o cerrada) la fuerza magnética sobre la corriente es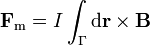
4.1 Demostración
Una corriente filiforme no es más que una corriente de volumen en el interior de un tubo. Podemos tomar como elemento de volumen un segmento de ese tubo, cumpliéndose 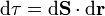 (volumen igual a base por altura), por lo que
(volumen igual a base por altura), por lo que

La integral sobre una sección del cable de la densidad de corriente no es otra cosa que la intensidad de corriente I. Por tanto





