Péndulo doble (CMR)

De Laplace

(Diferencias entre revisiones)

Revisión de 18:56 2 ene 2021

Contenido

1 Enunciado
2 Ecuaciones de movimiento
3 Aproximación para ángulos pequeños
- 3.1 Sistema de ecuaciones
- 3.2 Modos normales

1 Enunciado

Se tiene un péndulo doble plano. Está formado por una varilla rígida OA de masa despreciable y longitud 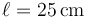$\ell=25\,\mathrm{cm}$ articulada en O y en cuyo extremo A se encuentra una masa 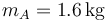$m_A=1.6\,\mathrm{kg}$ . En A se halla articulada una segunda varilla AB, de masa también despreciable, de la misma longitud math>\ell=25\,\mathrm{cm}</math> y en cuyo extremo B se encuentra una segunda masa de valor 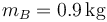$m_B=0.9\,\mathrm{kg}$ . 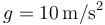Tómese $g = 10\,\mathrm{m}/\mathrm{s}^2$ .

Determine las ecuaciones de movimiento para los ángulos $φ$ , queg forma OA con la vertical, y θ que forma AB con la prolongación de OA. Sugerencia: empléense los cálculos del problema “Dos barras articuladas”
Suponiendo que las dos varillas realizan oscilaciones muy próximas a la vetical, de manera que 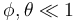$\phi,\theta\ll 1$ , calcule las frecuencias de los modos normales de oscilación. ¿Cómo oscilan las varillas en cada uno de los modos normales.
Imaginemos que, estando las varillas en reposo, se sujeta la masa A y la varilla AB se coloca con una inclinación de 5º con respecto a la vertical. Entonces, se sueltan las dos masas. ¿Cómo es el movimiento posterior de cada una de ellas?

2 Ecuaciones de movimiento

2.1 Para la masa A

Siguiendo los cálculos y la notación del problema “Dos barras articuladas” la segunda ley de Newton para la partícula A es

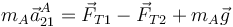
$m_A \vec{a}^A_{21}=\vec{F}_{T1}-\vec{F}_{T2}+m_A\vec{g}$

siendo 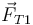$\vec{F}_{T1}$ la tensión de la varilla OA, que va dirigida a lo largo de la propia varilla

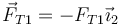
$\vec{F}_{T1}=-F_{T1}\vec{\imath}_2$

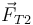$\vec{F}_{T2}$ la tensión de la varilla AB. En el extremo B tira hacia a A y en el extremo A tira hacia B.

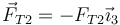
$\vec{F}_{T2}=-F_{T2}\vec{\imath}_3$

Por su parte, el peso va en la dirección del eje OX positivo

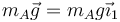
$m_A\vec{g}=m_A g\vec{\imath}_1$

La aceleración de A, tal como se ve en el problema mencionado, es

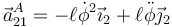
$\vec{a}^A_{21}=-\ell\dot{\phi}^2\vec{\imath}_2+\ell\ddot{\phi}\vec{\jmath}_2$

Todo esto nos da la ecuación

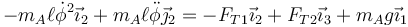
$-m_A\ell\dot{\phi}^2\vec{\imath}_2+m_A\ell\ddot{\phi}\vec{\jmath}_2=-F_{T1}\vec{\imath}_2+F_{T2}\vec{\imath}_3+m_Ag\vec{\imath}_1$

2.2 Para la masa B

La segunda ley de Newton en este caso es

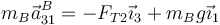
$m_B \vec{a}^B_{31}=-F_{T2}\vec{\imath}_3+m_Bg\vec{\imath}_1$

siendo la aceleración de B

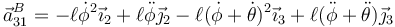
$\vec{a}^B_{31}=-\ell\dot{\phi}^2\vec{\imath}_2+\ell\ddot{\phi}\vec{\jmath}_2-\ell(\dot{\phi}+\dot{\theta})^2\vec{\imath}_3+\ell(\ddot{\phi}+\ddot{\theta})\vec{\jmath}_3$

lo que nos da la ecuación de movimiento

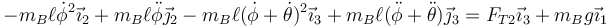
$-m_B\ell\dot{\phi}^2\vec{\imath}_2+m_B\ell\ddot{\phi}\vec{\jmath}_2-m_B\ell(\dot{\phi}+\dot{\theta})^2\vec{\imath}_3+m_B\ell(\ddot{\phi}+\ddot{\theta})\vec{\jmath}_3=F_{T2}\vec{\imath}_3+m_Bg\vec{\imath}_1$

2.3 Para los ángulos

En las ecuaciones anteriores podemos eliminar las tensiones, que son cantidades desconocidas, proyectando en las direcciones ortogonales. Así, en la ecuación de movimiento para B multiplicamos escalarmente por 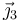$\vec{\jmath}_3$ y resulta

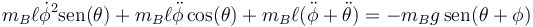
$m_B\ell\dot{\phi}^2\mathrm{sen}(\theta)+m_B\ell\ddot{\phi}\cos(\theta)+m_B\ell(\ddot{\phi}+\ddot{\theta})=-m_Bg\,\mathrm{sen}(\theta+\phi)$

Los productos escalares entre los vectores de las diferentes bases se deducen en el problema de cinemática ya citado.

Para eliminar la tensión de la varilla OA primero sumamos las dos ecuaciones de movimiento. De esta forma se elimina la tensión de la varilla AB, que es una fuerza interna, y queda

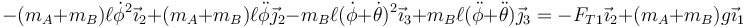
$-(m_A+m_B)\ell\dot{\phi}^2\vec{\imath}_2+(m_A+m_B)\ell\ddot{\phi}\vec{\jmath}_2-m_B\ell(\dot{\phi}+\dot{\theta})^2\vec{\imath}_3+m_B\ell(\ddot{\phi}+\ddot{\theta})\vec{\jmath}_3=-F_{T1}\vec{\imath}_2+(m_A+m_B)g\vec{\imath}_1$

Si aquí multiplicamos escalarmente por 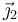$\vec{\jmath}_2$ resulta

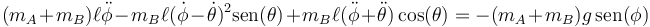
$(m_A+m_B)\ell\ddot{\phi}-m_B\ell(\dot{\phi}-\dot{\theta})^2\mathrm{sen}(\theta)+m_B\ell(\ddot{\phi}+\ddot{\theta})\cos(\theta)=-(m_A+m_B)g\,\mathrm{sen}(\phi)$

Podemos escribir estas ecuaciones de una manera menos engorrosa definiendo los parámetros

$\Omega=\sqrt{\frac{g}{\ell}}\qquad\qquad \gamma = \frac{m_B}{m_A}$

y resulta el sistema

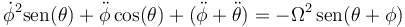
$\dot{\phi}^2\mathrm{sen}(\theta)+\ddot{\phi}\cos(\theta)+(\ddot{\phi}+\ddot{\theta})=-\Omega^2\,\mathrm{sen}(\theta+\phi)$

y

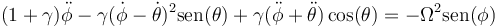
$(1+\gamma)\ddot{\phi}-\gamma(\dot{\phi}-\dot{\theta})^2\mathrm{sen}(\theta)+\gamma(\ddot{\phi}+\ddot{\theta})\cos(\theta)=-\Omega^2 \mathrm{sen}(\phi)$

3 Aproximación para ángulos pequeños

3.1 Sistema de ecuaciones

El sistema de ecuaciones general para cualquier valor de los ángulos y las masas no posee solución analítica y es preciso recurrir a métodos numéricos para obtener la solución en casos particulares.

Si los ángulos de desviación respecto a la vertical son pequeños, podemos hacer la llamada aproximación lineal, en la cual se desprecian las potencias de grado superior al primero.

En la misma aproximación

$\mathrm{sen}(\alpha)\simeq \alpha\qquad\qquad \cos(\alpha)\simeq 1$

En ese caso, la primera de las dos ecuaciones se aproxima por

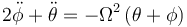
$2\ddot{\phi}+\ddot{\theta}=-\Omega^2\,(\theta+\phi)$

y la segunda

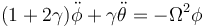
$(1+2\gamma)\ddot{\phi}+\gamma\ddot{\theta}=-\Omega^2 \phi$

En estas ecuaciones podemos despejar las aceleraciones angulares y queda

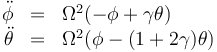
$\begin{array}{rcl} \ddot{\phi}&=&\Omega^2 (-\phi+\gamma\theta)\\ \ddot{\theta}&=&\Omega^2(\phi-(1+2\gamma)\theta) \end{array}$

o, en forma matricial,

No se pudo entender (Falta el ejecutable de texvc. Por favor, lea math/README para configurarlo.): \frac{\mathrm{d}\ }{\mathrm{d}t}\begin{matrix}\phi\\ \theta\end{pmatrix}=\Omega^2 \begin{pmatrix} -1 & \gamma \\ 1 & -(1+2\gamma)\end{pmatrix}\cdot\begin{matrix}\phi\\ \theta\end{pmatrix}

3.2 Modos normales

Este es un sistema de ecuaciones que se puede resolver mediante la búsqueda de sus modos normales. Se trata de buscar soluciones exponenciales

No se pudo entender (Falta el ejecutable de texvc. Por favor, lea math/README para configurarlo.): \begin{matrix}\phi\\ \theta\end{pmatrix} = \begin{matrix}\hat{\phi}\\ \hat{\theta}\end{pmatrix}\mathrm{e}^{\mathrm{j}\omega t}

La solución general es una combinación lineal de todos los modos normales posibles.

Sustituyendo esta solución en el sistema de ecuaciones diferenciales queda la ecuación algebraica

No se pudo entender (Falta el ejecutable de texvc. Por favor, lea math/README para configurarlo.): \begin{pmatrix} \Omega^2-\omega^2 & -\gamma \Omega^2\\ -\Omega^2 & (1+2\gamma)\Omega^2-\omega^2\end{pmatrix}\cdot\begin{matrix}\hat{\phi}\\ \hat{\theta}\end{pmatrix}=\begin{matrix}0\\ 0\end{pmatrix}

Para que este sistema tenga solución no trivial debe anularse el determinante

No se pudo entender (Falta el ejecutable de texvc. Por favor, lea math/README para configurarlo.): \left|\begin{matrix} \Omega^2-\omega^2 & -\gamma \Omega^2\\ -\Omega^2 & (1+2\gamma)\Omega^2-\omega^2\end{pmatrix}\cdot\begin{matrix}\hat{\phi}\\ \hat{\theta}\end{matrix}\right|=0

Esto nos da la ecuación de cuarto grado

ω 4 - 2(1 + γ)Ω 2 ω 2 + (1 + γ)Ω 4 = 0

Esta ecuación es, en realidad, una ecuación de segundo frado en ω², con soluciones

No se pudo entender (Falta el ejecutable de texvc. Por favor, lea math/README para configurarlo.): \omega^2 = \Omega^2 (1+\gamma\p,\sqrt{\gamma(1+\gamma)})

@@ Línea 99: / Línea 99: @@
 o, en forma matricial,
-<center><math>\frac{\mathrm{d}\ }{\mathrm{d}t}\begin{\pmatrix}\phi\\ \theta\end{pmatrix}=\Omega^2 \begin{pmatrix}
+<center><math>\frac{\mathrm{d}\ }{\mathrm{d}t}\begin{matrix}\phi\\ \theta\end{pmatrix}=\Omega^2 \begin{pmatrix}
--1 & \gamma \\ 1 & -(1+2\gamma)\end{pmatrix}\cdot\begin{\pmatrix}\phi\\ \theta\end{pmatrix}</math></center>
+-1 & \gamma \\ 1 & -(1+2\gamma)\end{pmatrix}\cdot\begin{matrix}\phi\\ \theta\end{pmatrix}</math></center>
 ===Modos normales===
 Este es un sistema de ecuaciones que se puede resolver mediante la búsqueda de sus modos normales. Se trata de buscar soluciones exponenciales
-<center><math>\begin{\pmatrix}\phi\\ \theta\end{pmatrix} = \begin{\pmatrix}\hat{\phi}\\ \hat{\theta}\end{pmatrix}\mathrm{e}^{\mathrm{j}\omega t}</math></center>
+<center><math>\begin{matrix}\phi\\ \theta\end{pmatrix} = \begin{matrix}\hat{\phi}\\ \hat{\theta}\end{pmatrix}\mathrm{e}^{\mathrm{j}\omega t}</math></center>
 La solución general es una combinación lineal de todos los modos normales posibles.
@@ Línea 111: / Línea 111: @@
 <center><math> \begin{pmatrix}
-\Omega^2-\omega^2 & -\gamma \Omega^2\\ -\Omega^2 & (1+2\gamma)\Omega^2-\omega^2\end{pmatrix}\cdot\begin{\pmatrix}\hat{\phi}\\ \hat{\theta}\end{pmatrix}=\begin{\pmatrix}0\\ 0\end{pmatrix}</math></center>
+\Omega^2-\omega^2 & -\gamma \Omega^2\\ -\Omega^2 & (1+2\gamma)\Omega^2-\omega^2\end{pmatrix}\cdot\begin{matrix}\hat{\phi}\\ \hat{\theta}\end{pmatrix}=\begin{matrix}0\\ 0\end{pmatrix}</math></center>
 Para que este sistema tenga solución no trivial debe anularse el determinante
 <center><math>\left|\begin{matrix}
-\Omega^2-\omega^2 & -\gamma \Omega^2\\ -\Omega^2 & (1+2\gamma)\Omega^2-\omega^2\end{pmatrix}\cdot\begin{\pmatrix}\hat{\phi}\\ \hat{\theta}\end{matrix}\right|=0</math></center>
+\Omega^2-\omega^2 & -\gamma \Omega^2\\ -\Omega^2 & (1+2\gamma)\Omega^2-\omega^2\end{pmatrix}\cdot\begin{matrix}\hat{\phi}\\ \hat{\theta}\end{matrix}\right|=0</math></center>
 Esto nos da la ecuación de cuarto grado

Péndulo doble (CMR)

De Laplace

Revisión de 18:56 2 ene 2021

Contenido

1 Enunciado

2 Ecuaciones de movimiento

2.1 Para la masa A

2.2 Para la masa B

2.3 Para los ángulos

3 Aproximación para ángulos pequeños

3.1 Sistema de ecuaciones

3.2 Modos normales

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES