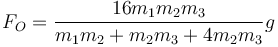Entrar Página Discusión Historial Go to the site toolbox

Doble máquina de Atwood

De Laplace

(Diferencias entre revisiones)
(→Solución)
Línea 1: Línea 1:
==Enunciado==
==Enunciado==
-
La doble máquina de Atwood de la figura está formada por tres masas unidas a través de dos cuerdas ideales (inextensibles y sin masa) y dos poleas también ideales (de masa despreciable y sin rozamiento). Determine la aceleración de cada una de las masas, así como las tensiones de las dos cuerdas.
+
Una máquina de Atwood es un dispositivo simple compuesto por una polea por la que pasa una cuerda, de cuyos extremos penden dos masas <math>m_1</math> y <math>m_2</math>. En el caso ideal se supone que la cuerda es inextensible y sin masa, y que la polea tampoco tiene masa ni fricción. La doble máquina de Atwood de la figuraestá formada por tres masas unidas a través de dos cuerdas ideales y dos poleas también ideales. Determine:
-
 
+
# La aceleración de cada una de las masas
-
<center>[[Archivo:doble-maquina-atwood.png]]</center>
+
# Las tensiones de las dos cuerdas.
 +
# La fuerza que ejerce el gancho del que cuelga el sistema.
 +
[[Archivo:atwood-doble.png]]
==Solución==
==Solución==
-
[[Archivo:doble-atwood-z.png|right]]
+
En este sistema, sobre cada masa actúa su peso y la tensión de la cuerda que lo sostiene.
 +
Tomamos el eje OX como vertical y hacia abajo, con el origen en el centro de la polea superior.
 +
Dado que el movimiento es puramente rectilíneo, podemos usar cantidades escalares. En este caso, la segunda ley de Newton para las tres masas nos da
 +
<center><math>\begin{array}{rcl}
 +
m_1a_1&=&m_1g-F_{T1}\\
 +
m_2a_2&=&m_2g-F_{T2}\\
 +
m_3a_3&=&m_3g-F_{T3}
 +
\end{array}</math></center>
 +
Aquí tenemos tres ecuaciones, pero 6 incógnitas, ya que las 3 tensiones tamnién son desconocidas (NO son iguales al peso).
-
Considerando los diagramas de cuerpo libre, tenemos lo siguiente:
+
Para ello, debemos aplicar las ecuaciones de vínculos, que se refieren a la existencia de los hilos que unen las masas.
-
[[Archivo:doble-atwood-mi.png|left]] Sobre la masa <math>m_1</math> actúa la tensión de la cuerda y su peso, por lo que
+
Por ser de masa nula, las tensiones de cada hilo son del mismo módulo en todos sus puntos (pero no iguales las del primer hilo a las del segundo). Aplicando esto al hilo que une las masas 2 y 3
-
<center><math>\vec{T}_1 + m_1\vec{g} = m_1\vec{a}_1</math></center>
+
<center><math>F_{T2}=F_{T3}\,</math></center>
-
dado que todas las fuerzas y aceleraciones en este problema son verticales, podemos usar cantidades escalares y escribir
+
Para relacionar estas tensiones con las del otro hilo, <math>F_{T1}</math>, analizamos la 2ª ley de Newton para la polea pequeña. Al ser ideal es de masa nula, por lo que
-
<center><math>T_1-m_1g = m_1a_1\,</math></center>
+
<center><math>\overbrace{m_0}^{=0}a_2=F_{T2}+F_{T3}-F_{T1}\qquad\Rightarrow\qquad F_{T1}=F_{T2}+F_{T3}</math></center>
-
La aceleración de la masa 1 (y análogamente la de las otras dos masas) es la segunda derivada temporal de posición, que en el caso del movimiento vertical se reduce a
+
Obsérvese que esta polea se está moviendo, pero al ser de masa nula no tiene inercia, por lo que la suma de las fuerzas debe anularse (si no, saldría una aceleración infinita).
-
<center><math>a_1 = \frac{\mathrm{d}^2z_1}{\mathrm{d}t^2}</math></center>
+
Ya tenemos 5 ecuaciones. La sexta sale de que los hilos son inextensibles, por lo tanto, la suma de los diferentes tramos de cada hilo debe salir una constante.
-
Para la masa 2 tenemos, de manera análoga
+
Si llamamos x_0 a la posición en que se encuentra la polea pequeña, se cumple, para el primer hilo
-
<center><math>T_2 - m_2g = m_2a_2\,</math></center>
+
<center><math>x_1+x_0 = \ell_1 = \mathrm{cte}</math></center>
-
y para la 3
+
Para el segundo hilo, el que pasa por la polea móvil, la longitud de los dos tramos es, respectivamente, <math>(x_2-x_0)</math> (a la izquierda) y <math>(x_3-x_0)</math> (a la derecha), por lo que tenemos la ecuación
-
<center><math>T_3 - m_3g = m_3a_3\,</math></center>
+
<center><math>(x_2-x_0)+(x_3-x_0)= x_2+x_3-2x_0=\ell_2</math></center>
-
Por el hecho de tratarse de cuerdas ideales, inextensibles y sin masa, la tensión en la cuerda que ata las masas 2 y 3 es la misma en todos sus puntos, por lo que
+
Sumando esta ecuación con el doble de la anterior llegamos a la relación entre las posiciones
-
<center><math>T_2 = T_3\,</math></center>
+
<center><math>x_2+x_3+2x_1=\ell_2+2\ell_1=\mathrm{cte.}</math></center>
-
[[Archivo:doble-atwood-polea.png|left]]
+
Derivando aquí dos veces respecto al tiempo, obtenemos una relación entre las aceleraciones
-
Ahora bien, ¿cómo se relacionan estas dos tensiones con <math>T_1</math>, la tensión de la otra cuerda. Para obtenerlo escribimos la ecuación de movimiento para esta polea, para la que suponemos provisionalmente una masa <math>m_0</math>. Sobre esta polea actúan tres tensiones además del peso, siendo una de ellas igual a la que actúa sobre la masa 1.
+
<center><math>a_2+a_3+2a_1=0\,</math></center>
-
<center><math>T_0 - T_2-T_3 - m_0g = m_0a_0\,</math></center>
+
Tenemos entonces el siguiente sistema de 6 ecuaciones con 6 incógnitas
-
Al ser una polea ideal, su masa es nula, por lo que nos queda la relación de equilibrio
+
<center><math>\begin{array}{rcl}
 +
m_1a_1&=&m_1g-F_{T1}\\
 +
m_2a_2&=&m_2g-F_{T2}\\
 +
m_3a_3&=&m_3g-F_{T3} \\
 +
F_{T2}&=&F_{T3}\\
 +
F_{T1}&=&F_{T2}+F_{T3}\\
 +
a_2+a_3+2a_1&=&0
 +
\end{array}</math></center>
-
<center><math>T_0 - T_2 - T_3 = 0\qquad\Rightarrow\qquad T_0=2T_2\,</math></center>
+
Al ser un sistema lineal puede resolverse de múltiples maneras. Por ejemplo, podemos despejar las tensiones
-
Como por otro lado, esta polea y la masa 1 está unidas por la misma cuerda
+
<center><math>F_{T1} = m_1(g-a_1)\qquad F_{T2}=m_2(g-a_2)\qquad\qquad F_{T3}=m_3(g-a_3)</math></center>
-
<center><math>T_1=T_0=2T_2\,</math></center>
+
y dado que, de las relaciones entre las tensiones
-
Las cuerdas son inextensibles, lo que permite relacionar las aceleraciones. En este caso no es cierto que la aceleración con la que sube <math>m_2</math> sea la misma que con la que baja <math>m_3</math> ya que ambas penden de un punto que también se mueve aceleradamente.
+
<center><math>F_{T1}=2F_{T2}\qquad\qquad F_{T1}=2F_{T3}</math></center>
-
Si la polea superior se encuentra a una altura <math>H</math> respecto al suelo, las masas se encuentran a alturas <math>z_1</math>, <math>z_2</math> y <math>z_3</math> respectivamente, y la polea pequeña a una altura <math>z_0</math>, la longitud de la cuerda que la une con la masa 1 es
+
llegamos a las relaciones
-
<center><math>L_1 = (H-z_1) + (H-z_0)+\pi R_1\,</math></center>
+
<center><math>m_1(g-a_1)=2m_2(g-a_2)\qquad\qquad m_1(g-a_1)=2m_3(g-a_3)</math></center>
-
Derivando esta ecuación dos veces respecto al tiempo
+
Despejamos aquí
-
<center><math>0=-\frac{\mathrm{d}^2z_1}{\mathrm{d}t^2}-\frac{\mathrm{d}^2z_0}{\mathrm{d}t^2}\qquad\Rightarrow\qquad a_0 = -a_1</math></center>
+
<center><math>a_2 = \left(1-\frac{m_1}{2m_2})g+\frac{m_1}{2m_2}a_1\qquad\qquad a_3 = \left(1-\frac{m_1}{2m_3})g+\frac{m_1}{2m_3}a_1</math></center>
-
Por su parte la longitud de la cuerda que pasa por la polea pequeña vale
+
Sustituimos en la relación entre las aceleraciones
-
<center><math>L_2 = (z_0-z_2)+(z_0-z_3)+\pi R\,</math></center>
+
<center><math>\left(1-\frac{m_1}{2m_2})g+\frac{m_1}{2m_2}a_1+\left(1-\frac{m_1}{2m_3})g+\frac{m_1}{2m_3}a_1+2a_1=0</math></center>
-
que tras derivar nos da
+
lo que nos da finalmente, despejando,
-
<center><math>2a_0 = a_2+a_3\,</math></center>
+
<center><math>a_1=\dfrac{m_1m_2+m_2m_3-4m_2m_3}{m_1m_2+m_2m_3+4m_2m_3}g</math></center>
-
Ya tenemos información suficiente para hallar las aceleraciones. Tenemos el sistema
+
Una vez que tenemos la aceleración de la masa 1, obtenemos las otras dos
-
 
+
-
<center><math>\begin{array}{rcl}
+
-
T_1-m_1g & = & m_1a_1\\
+
-
T_2-m_2g & = & m_2a_2\\
+
-
T_3-m_3g & = & m_3a_3\\
+
-
T_1 & = & T_2+T_3\\
+
-
T_2 & = & T_3\\
+
-
2a_1 & = & -a_2-a_3
+
-
\end{array}</math></center>
+
-
Despejando y sustituyendo llegamos a los resultados
+
<center><math>a_2=\frac{m_1 m_2 - 3 m_1 m_3 + 4 m_2 m_3}{m_1m_2+m_2m_3+4m_2m_3}g\qquad\qquad a_3=\frac{-3m_1 m_2 +  m_1 m_3 + 4 m_2 m_3}{m_1m_2+m_2m_3+4m_2m_3}g</math></center>
-
<center><math>a_1=\frac{4m_2m_3-m_1m_2-m_1m_3}{4m_2m_3+m_1m_2+m_1m_3}g</math>{{qquad}}{{qquad}}<math>a_2=\frac{3m_1m_3-m_1m_2-4m_2m_3}{4m_2m_3+m_1m_2+m_1m_3}g</math>{{qquad}}{{qquad}}<math>a_3=\frac{3m_1m_2-m_1m_3-4m_2m_3}{4m_2m_3+m_1m_2+m_1m_3}g</math></center>
+
y, conocidas las aceleraciones obtenemos las tensiones
 +
<center><math>F_{T2}=F_{T3}=\frac{4m_1m_2m_3}{m_1m_2+m_2m_3+4m_2m_3}g\qquad \qquad F_{T1}=\frac{8m_1m_2m_3}{m_1m_2+m_2m_3+4m_2m_3}g</math></center>
 +
La fuerza que hace el soporte de la polea superior es igual al doble de la tensión de la cuerda que pasa por ella
-
[[Categoría:Problemas de dinámica de la partícula (GIE)]]
+
<center><math>F_O=\frac{16m_1m_2m_3}{m_1m_2+m_2m_3+4m_2m_3}g</math></center>

Revisión de 11:16 17 nov 2020

1 Enunciado

Una máquina de Atwood es un dispositivo simple compuesto por una polea por la que pasa una cuerda, de cuyos extremos penden dos masas m1 y m2. En el caso ideal se supone que la cuerda es inextensible y sin masa, y que la polea tampoco tiene masa ni fricción. La doble máquina de Atwood de la figuraestá formada por tres masas unidas a través de dos cuerdas ideales y dos poleas también ideales. Determine:

  1. La aceleración de cada una de las masas
  2. Las tensiones de las dos cuerdas.
  3. La fuerza que ejerce el gancho del que cuelga el sistema.

Archivo:atwood-doble.png

2 Solución

En este sistema, sobre cada masa actúa su peso y la tensión de la cuerda que lo sostiene. Tomamos el eje OX como vertical y hacia abajo, con el origen en el centro de la polea superior. Dado que el movimiento es puramente rectilíneo, podemos usar cantidades escalares. En este caso, la segunda ley de Newton para las tres masas nos da

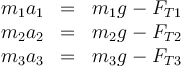
\begin{array}{rcl} m_1a_1&=&m_1g-F_{T1}\\ m_2a_2&=&m_2g-F_{T2}\\ m_3a_3&=&m_3g-F_{T3} \end{array}

Aquí tenemos tres ecuaciones, pero 6 incógnitas, ya que las 3 tensiones tamnién son desconocidas (NO son iguales al peso).

Para ello, debemos aplicar las ecuaciones de vínculos, que se refieren a la existencia de los hilos que unen las masas.

Por ser de masa nula, las tensiones de cada hilo son del mismo módulo en todos sus puntos (pero no iguales las del primer hilo a las del segundo). Aplicando esto al hilo que une las masas 2 y 3

F_{T2}=F_{T3}\,

Para relacionar estas tensiones con las del otro hilo, FT1, analizamos la 2ª ley de Newton para la polea pequeña. Al ser ideal es de masa nula, por lo que

\overbrace{m_0}^{=0}a_2=F_{T2}+F_{T3}-F_{T1}\qquad\Rightarrow\qquad F_{T1}=F_{T2}+F_{T3}

Obsérvese que esta polea se está moviendo, pero al ser de masa nula no tiene inercia, por lo que la suma de las fuerzas debe anularse (si no, saldría una aceleración infinita).

Ya tenemos 5 ecuaciones. La sexta sale de que los hilos son inextensibles, por lo tanto, la suma de los diferentes tramos de cada hilo debe salir una constante.

Si llamamos x_0 a la posición en que se encuentra la polea pequeña, se cumple, para el primer hilo

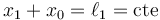
x_1+x_0 = \ell_1 = \mathrm{cte}

Para el segundo hilo, el que pasa por la polea móvil, la longitud de los dos tramos es, respectivamente, (x2 − x0) (a la izquierda) y (x3 − x0) (a la derecha), por lo que tenemos la ecuación

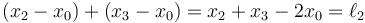
(x_2-x_0)+(x_3-x_0)= x_2+x_3-2x_0=\ell_2

Sumando esta ecuación con el doble de la anterior llegamos a la relación entre las posiciones

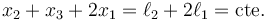
x_2+x_3+2x_1=\ell_2+2\ell_1=\mathrm{cte.}

Derivando aquí dos veces respecto al tiempo, obtenemos una relación entre las aceleraciones

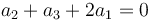
a_2+a_3+2a_1=0\,

Tenemos entonces el siguiente sistema de 6 ecuaciones con 6 incógnitas

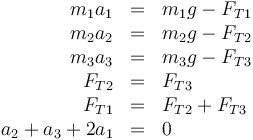
\begin{array}{rcl} m_1a_1&=&m_1g-F_{T1}\\ m_2a_2&=&m_2g-F_{T2}\\ m_3a_3&=&m_3g-F_{T3} \\ F_{T2}&=&F_{T3}\\ F_{T1}&=&F_{T2}+F_{T3}\\ a_2+a_3+2a_1&=&0 \end{array}

Al ser un sistema lineal puede resolverse de múltiples maneras. Por ejemplo, podemos despejar las tensiones

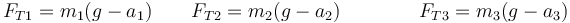
F_{T1} = m_1(g-a_1)\qquad F_{T2}=m_2(g-a_2)\qquad\qquad F_{T3}=m_3(g-a_3)

y dado que, de las relaciones entre las tensiones

F_{T1}=2F_{T2}\qquad\qquad F_{T1}=2F_{T3}

llegamos a las relaciones

m_1(g-a_1)=2m_2(g-a_2)\qquad\qquad m_1(g-a_1)=2m_3(g-a_3)

Despejamos aquí

No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): a_2 = \left(1-\frac{m_1}{2m_2})g+\frac{m_1}{2m_2}a_1\qquad\qquad a_3 = \left(1-\frac{m_1}{2m_3})g+\frac{m_1}{2m_3}a_1

Sustituimos en la relación entre las aceleraciones

No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \left(1-\frac{m_1}{2m_2})g+\frac{m_1}{2m_2}a_1+\left(1-\frac{m_1}{2m_3})g+\frac{m_1}{2m_3}a_1+2a_1=0

lo que nos da finalmente, despejando,

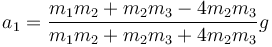
a_1=\dfrac{m_1m_2+m_2m_3-4m_2m_3}{m_1m_2+m_2m_3+4m_2m_3}g

Una vez que tenemos la aceleración de la masa 1, obtenemos las otras dos

a_2=\frac{m_1 m_2 - 3 m_1 m_3 + 4 m_2 m_3}{m_1m_2+m_2m_3+4m_2m_3}g\qquad\qquad a_3=\frac{-3m_1 m_2 + m_1 m_3 + 4 m_2 m_3}{m_1m_2+m_2m_3+4m_2m_3}g

y, conocidas las aceleraciones obtenemos las tensiones

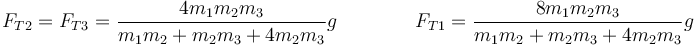
F_{T2}=F_{T3}=\frac{4m_1m_2m_3}{m_1m_2+m_2m_3+4m_2m_3}g\qquad \qquad F_{T1}=\frac{8m_1m_2m_3}{m_1m_2+m_2m_3+4m_2m_3}g

La fuerza que hace el soporte de la polea superior es igual al doble de la tensión de la cuerda que pasa por ella

F_O=\frac{16m_1m_2m_3}{m_1m_2+m_2m_3+4m_2m_3}g
Obtenido de "http://tesla.us.es/wiki/index.php/Doble_m%C3%A1quina_de_Atwood"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace