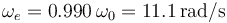Muelle forzado
De Laplace
(→Enunciado) |
|||
| Línea 1: | Línea 1: | ||
== Enunciado == | == Enunciado == | ||
| - | Una pesa de 1.50 kg está suspendida de un muelle con una constante elástica <math>k=200\,\mathrm{N/m}</math>. Una fuerza sinusoidal con una magnitud de 1.70 N excita el sistema. ¿Que frecuencia debe tener la fuerza externa para que el objeto vibre con una amplitud de 0. | + | Una pesa de 1.50 kg está suspendida de un muelle con una constante elástica <math>k=200\,\mathrm{N/m}</math>. Una fuerza sinusoidal con una magnitud de 1.70 N excita el sistema. El factor de rozamiento es <math>\gamma=0.1\,\mathrm{s^{-1}}</math>¿Que frecuencia debe tener la fuerza externa para que el objeto vibre con una amplitud de 0.122 m? |
== Solución == | == Solución == | ||
Revisión de 11:20 3 may 2020
1 Enunciado
Una pesa de 1.50 kg está suspendida de un muelle con una constante elástica 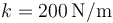 . Una fuerza sinusoidal con una magnitud de 1.70 N excita el sistema. El factor de rozamiento es
. Una fuerza sinusoidal con una magnitud de 1.70 N excita el sistema. El factor de rozamiento es 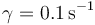 ¿Que frecuencia debe tener la fuerza externa para que el objeto vibre con una amplitud de 0.122 m?
¿Que frecuencia debe tener la fuerza externa para que el objeto vibre con una amplitud de 0.122 m?
2 Solución
Cuando un muelle está sometido a una fuerza externa periódica de frecuencia ωe, oscila con una frecuencia igual a la de la fuerza externa
x(t) = Acos(ωet + Φ)
La amplitud de la oscilación es
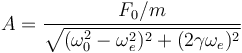
Aquí, F0 es la amplitud de la fuerza externa, 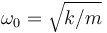 es la frecuencia propia del muelle y γ es el parámetro de rozamiento.
es la frecuencia propia del muelle y γ es el parámetro de rozamiento.
En este caso, no hay fuerza de rozamiento, por lo que la amplitud es
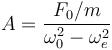
Despajando la frecuencia externa tenemos
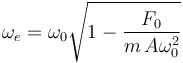
En el problema la frecuencia propia es
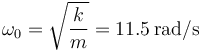
Por tanto la frecuencia externa necesaria es