Problemas de inducción electromagnética (GIOI)
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Barra que avanza en un campo uniforme== Una barra metálica de longitud <math>a=10\,\mathrm{cm}</math> se mueve en el interior de un campo magnético uniforme <math>\vec{B}_0<…') |
(→Barra que avanza en un campo uniforme) |
||
| Línea 10: | Línea 10: | ||
[[Barra que avanza en un campo uniforme|Solución]] | [[Barra que avanza en un campo uniforme|Solución]] | ||
| + | |||
| + | ==Espira cuadrada que gira en un campo magnético== | ||
| + | Una espira cuadrada de lado <math>a=2\,\mathrm{cm}</math>, de hilo de cobre de sección <math>A=0.5\,\mathrm{mm}^2</math> gira con frecuencia <math>f=400\,\mathrm{Hz}</math> en el interior de un campo magnético uniforme de módulo <math>B_0=200\,\mathrm{mT}</math>. El eje de giro es perpendicular al campo magnético. | ||
| + | |||
| + | <center>[[Image:cuadradorotante.gif]]</center> | ||
| + | |||
| + | # Determine la corriente que se induce en la espira. | ||
| + | # Calcule la potencia instantánea disipada en la espira y la energía total disipada en un periodo de giro. | ||
| + | # Calcule el par que en cada instante ejerce el campo magnético sobre la espira. | ||
| + | # Para mantener la rotación constante, es necesario realizar un par opuesto al anterior. ¿Cuánto vale la potencia desarrollada por el par externo y el trabajo total realizado para mantener la rotación? | ||
| + | |||
| + | |||
| + | [[Espira cuadrada que gira en un campo magnético (GIOI)|Solución]] | ||
| + | |||
| + | ==Frenado magnético de espira== | ||
| + | Una espira cuadrada de lado <math>a=10\,\mathrm{cm}</math>, hecha de un hilo de cobre de sección <math>A=1\,\mathrm{mm}^2</math> penetra en un campo magnético uniforme perpendicular al plano de la espira y de módulo <math>B_0=30\,\mathrm{mT}</math>. La espira se mueve inicialmente con velocidad <math>v_0=0.5\,\mathrm{m}/\mathrm{s}</math> tangente a uno de sus lados y perpendicular al campo magnético. En <math>t=0</math> la espira entra en el campo. | ||
| + | |||
| + | <center>[[Image:cuadradoenB.gif]]</center> | ||
| + | |||
| + | # Calcule la corriente que se induce en la espira cuando la espira ha avanzado una distancia <math>x\,</math> y se está moviendo con velocidad <math>v\,</math>. | ||
| + | # Halle la fuerza que el campo magnético ejerce con la espira. | ||
| + | # Si la velocidad de la espira se mantiene constante, halle la potencia disipada en la espira por efecto Joule. ¿De dónde proviene la energía disipada? | ||
| + | # Si se deja que la espira frene por acción del campo magnético, determine la evolución en el tiempo de la velocidad, así como la energía total disipada por efecto Joule. | ||
| + | |||
| + | [[Frenado magnético de espira|Solución]] | ||
Revisión de 16:13 7 abr 2020
1 Barra que avanza en un campo uniforme
Una barra metálica de longitud 
se mueve en el interior de un campo magnético uniforme 
(
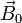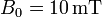) con velocidad constante 
, siendo perpendicular tanto al eje de la varilla como al campo magnético y de módulo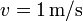 
.
- Calcule la fuerza magnética sobre una carga
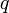de la varilla. ¿Hacia donde se mueven las cargas positivas y negativas de la varilla?
- La separación de carga alcanza el equilibrio cuando la fuerza eléctrica debido a dicha separación compensa exactamente la fuerza magnética. Usando esto, halle el campo eléctrico en el interior de la varilla.
- Calcule el voltaje entre los extremos de la varilla.
- Calcule la f.e.m. inducida, de acuerdo con la ley de Faraday, a lo largo de una curva formada por la varilla y un cierre por el exterior del campo magnético. Compruebe que coincide con el voltaje calculado en el apartado anterior.
2 Espira cuadrada que gira en un campo magnético
Una espira cuadrada de lado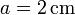 
, de hilo de cobre de sección 
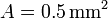gira con frecuencia 
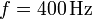en el interior de un campo magnético uniforme de módulo 
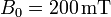. El eje de giro es perpendicular al campo magnético.
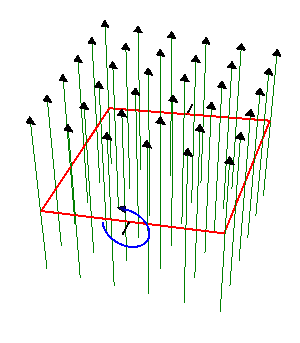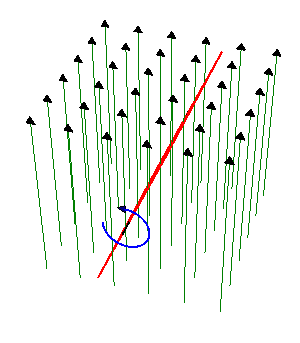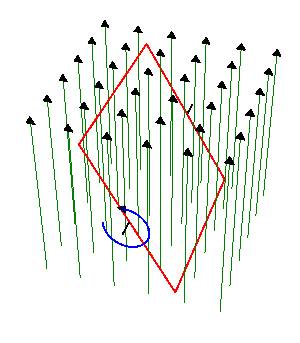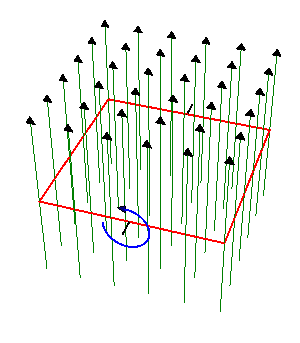
- Determine la corriente que se induce en la espira.
- Calcule la potencia instantánea disipada en la espira y la energía total disipada en un periodo de giro.
- Calcule el par que en cada instante ejerce el campo magnético sobre la espira.
- Para mantener la rotación constante, es necesario realizar un par opuesto al anterior. ¿Cuánto vale la potencia desarrollada por el par externo y el trabajo total realizado para mantener la rotación?
3 Frenado magnético de espira
Una espira cuadrada de lado , hecha de un hilo de cobre de sección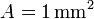 
penetra en un campo magnético uniforme perpendicular al plano de la espira y de módulo 
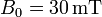. La espira se mueve inicialmente con velocidad 
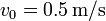tangente a uno de sus lados y perpendicular al campo magnético. En t = 0 la espira entra en el campo.
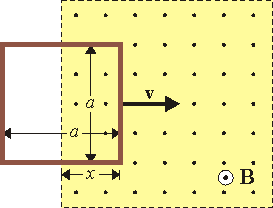
- Calcule la corriente que se induce en la espira cuando la espira ha avanzado una distancia
y se está moviendo con velocidad 
.
- Halle la fuerza que el campo magnético ejerce con la espira.
- Si la velocidad de la espira se mantiene constante, halle la potencia disipada en la espira por efecto Joule. ¿De dónde proviene la energía disipada?
- Si se deja que la espira frene por acción del campo magnético, determine la evolución en el tiempo de la velocidad, así como la energía total disipada por efecto Joule.
