Modelo esférico de generador

De Laplace

(Diferencias entre revisiones)

Revisión de 20:37 14 mar 2009

Contenido

1 Enunciado
2 Solución

1 Enunciado

Como modelo ideal de generador suponga el siguiente sistema: una esfera de radio $a$ de conductividad $σ 1$ se encuentra inmersa en un medio de conductividad $σ 2$ que se extiende hasta el infinito. En el interior de la esfera actúa una fuerza no electrostática por unidad de carga 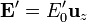$\mathbf{E}' = E'_0\mathbf{u}_{z}$ , constante y uniforme.

Escriba las ecuaciones y condiciones de salto para la densidad de corriente, el campo y el potencial eléctrico en todo el espacio.
Sabiendo que en el interior de la esfera el potencial es de la forma

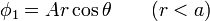
$\phi_1 = A r\cos\theta \qquad (r<a)$

y en el exterior de ella

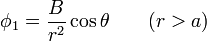
$\phi_1 = \frac{B}{r^2}\cos\theta \qquad (r>a)$

calcule las constantes

A

y

B

.

Halle la potencia desarrollada por el campo eléctrico en el interior y el exterior de la esfera.
Considerando que la corriente es la que atraviesa el plano ecuatorial de la esfera ( $z = 0$ , $r < a$ ) determine la fuerza electromotriz, la resistencia interna y la externa del circuito equivalente.
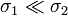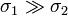¿A qué tienden los resultados cuando $\sigma_1 \ll \sigma_2$ ? ¿Y cuando $\sigma_1\gg \sigma_2$ ?

2 Solución

2.1 Ecuaciones y condiciones de salto

2.1.1 Ecuaciones

El sistema está formado por dos regiones: la interior (“1”) en $r < a$ , y la exterior (“2”) en $r > a$ . En cada una de ellas tendremos un cierto campo eléctrico 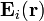$\mathbf{E}_i(\mathbf{r})$ , que debemos determinar.

Por tratarse de una situación estacionaria, el campo eléctrico en cada región es irrotacional

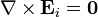
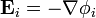
$\nabla\times\mathbf{E}_i = \mathbf{0}\,$ $\Rightarrow$ $\mathbf{E}_i=-\nabla\phi_i\,$

Igualmente, por ser la corrientes estacionarias, las densidades de corriente cumplen

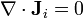
$\nabla\cdot\mathbf{J}_i=0\,$

Para completar estas relaciones, precisamos de las relaciones constitutivas, que indicamos después.

2.1.2 Condiciones de salto

En la frontera entre las dos regiones debe cumplirse la continuidad de la componente tangencial del campo eléctrico, que implica la continuidad del potencial eléctrico

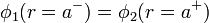
$\mathbf{n}\times[\mathbf{E}]=\mathbf{0}\qquad(r=a)$ $\Rightarrow$ $\phi_1(r=a^-)=\phi_2(r=a^+)\,$

Por ser una situación estacionaria, no hay variación en la carga superficial y, por tratarse de materiales óhmicos, tampoco hay corrientes superficiales, con lo que la condición de salto para la densidad de corriente se reduce a

$\mathbf{n}\cdot[\mathbf{J}]=0\qquad(r=a)$

En esta condición de salto y en la anterior, el vector $\mathbf{n}$ es el normal a la superficie esférica, esto es

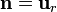
$\mathbf{n}=\mathbf{u}_r\,$

Además de estas condiciones de salto hay que imponer que el potencial eléctrico tiende a 0 en el infinito y que no es singular en el centro de la esfera 8en el que no hay carga puntual alguna)

$\phi_2\to 0\qquad(r\to\infty)$ $\phi_1\not\to\infty\qquad (r\to 0)$

2.1.3 Relaciones constitutivas

Para completar las ecuaciones y condiciones anteriores, necesitamos ecuaciones que liguen la densidad de corriente con el campo eléctrico.

En el exterior del generador esférico, la relación es simplemente la ley de Ohm

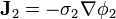
$\mathbf{J}_2=\sigma_2\mathbf{E}_2\,$ $\Rightarrow$ $\mathbf{J}_2=-\sigma_2\nabla\phi_2\,$

En el interior del generador no se cumple la ley de ohm, ya que las cargas no son movidas solamente por el campo electrostático, sino que también actúa sobre ellas el campo efectivo 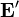$\mathbf{E}'$ que es el que consigue vencer al campo eléctrico y separar las cargas. La densidad de corriente estará asociada a la superposición de estos efectos

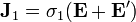
$\mathbf{J}_1=\sigma_1(\mathbf{E}+\mathbf{E}')\,$

2.1.4 Ecuaciones para el potencial

Combinando todo lo anterior podemos expresar el problema como uno para el potencial eléctrico. Tenemos que en el exterior del generador el potencial cumple la ecuación de Laplace

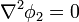
$0 = \nabla\cdot\mathbf{J}_2=-\nabla\cdot(\sigma_2\nabla\phi)$ $\Rightarrow$ $\nabla^2\phi_2=0\,$

En coordenadas esféricas queda

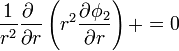
$\frac{1}{r^2}\frac{\partial\ }{\partial r}\left(r^2\frac{\partial\phi_2}{\partial r}\right)+ =0$

No se han incluido el término con derivadas en $\varphi$ porque, dada la simetría del sistema (de revolución en torno al eje Z), el potencial no va a depender de esta coordenada. Sí va a depender de $θ$ ya que no es lo mismo estar por el lado del ánodo que por el del cátodo.

En el interior también se cumple la ecuación de Laplace, por ser 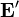$\mathbf{E}'$ un campo uniforme

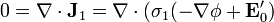
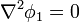
$0 = \nabla\cdot\mathbf{J}_1=\nabla\cdot(\sigma_1(-\nabla\phi+\mathbf{E}_0')$ $\Rightarrow$ $\nabla^2\phi_1=0\,$

y la expresión en coordenadas esféricas es idéntica a la que escribimos antes.

2.2 Potencial eléctrico

2.3 Potencia eléctrica

2.4 Circuito equivalente

2.5 Valores límite

@@ Línea 64: / Línea 64: @@
 En coordenadas esféricas queda
 <center>
-<math>\frac{1}{r^2}\frac{\partial\ }{\partial r}\left(r^2\frac{\partial\phi_2}{\partial r}\right)+\frac{1}{r^2\,\mathrm{sen}\,\theta}\left(\frac{\partial\ }{\partial\theta}\left(\mathrm{sen}\,\theta\,\frac{\partial\phi_2}{\partial\theta}\right)=0</math></center>
+<math>\frac{1}{r^2}\frac{\partial\ }{\partial r}\left(r^2\frac{\partial\phi_2}{\partial r}\right)+
+=0</math></center>
 No se han incluido el término con derivadas en <math>\varphi</math> porque, dada la simetría del sistema (de revolución en torno al eje Z), el potencial no va a depender de esta coordenada. Sí va a depender de <math>\theta</math> ya que no es lo mismo estar por el lado del ánodo que por el del cátodo.

Modelo esférico de generador

De Laplace

Revisión de 20:37 14 mar 2009

Contenido

1 Enunciado

2 Solución

2.1 Ecuaciones y condiciones de salto

2.1.1 Ecuaciones

2.1.2 Condiciones de salto

2.1.3 Relaciones constitutivas

2.1.4 Ecuaciones para el potencial

2.2 Potencial eléctrico

2.3 Potencia eléctrica

2.4 Circuito equivalente

2.5 Valores límite

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES