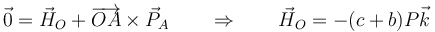Percusión sobre una barra articulada
De Laplace
(→Introducción=) |
|||
| (2 ediciones intermedias no se muestran.) | |||
| Línea 4: | Línea 4: | ||
¿Y sí en lugar de estar articulada, está empotrada en O? | ¿Y sí en lugar de estar articulada, está empotrada en O? | ||
| - | ==Introducción | + | ==Introducción== |
A diferencia del problema mencionado, en este existe un vínculo que limita el movimiento de la varilla. La articulación en O hace que el movimiento sea necesariamente una rotación alrededor de este punto. Esto relaciona la velocidad del CM con la velocidad angular | A diferencia del problema mencionado, en este existe un vínculo que limita el movimiento de la varilla. La articulación en O hace que el movimiento sea necesariamente una rotación alrededor de este punto. Esto relaciona la velocidad del CM con la velocidad angular | ||
| Línea 14: | Línea 14: | ||
siendo <math>\gamma=1</math> para una mancuerna (varilla sin masa, con dos masas en los extremos, en este caso una en la propia articulación) y <math>\gamma=1/3</math> para la barra homogénea. | siendo <math>\gamma=1</math> para una mancuerna (varilla sin masa, con dos masas en los extremos, en este caso una en la propia articulación) y <math>\gamma=1/3</math> para la barra homogénea. | ||
| + | |||
==Momento cinético respecto a O== | ==Momento cinético respecto a O== | ||
El teorema del momento cinético, aplicado en O, nos da | El teorema del momento cinético, aplicado en O, nos da | ||
| Línea 53: | Línea 54: | ||
lo que nos da | lo que nos da | ||
| - | <center><math>\vec{P}_O=\left(\frac{(b+c)P}{(\gamma+1)b}-P\right)\vec{\jmath | + | <center><math>\vec{P}_O=\left(\frac{(b+c)P}{(\gamma+1)b}-P\right)\vec{\jmath}=\frac{c-\gamma b}{(\gamma+1)b}\vec{P}_A</math></center> |
Para el caso de la mancuerna dado que c < 1, esta percusión de reacción siempre es opuesta a la que aplicamos, pero para la barra homogénea, puede tanto ir en sentido opuesto como en el mismo sentido, dependiendo del punto de aplicación. En particular, si <math>c=b/3</math>, la percusión de reacción es nula. | Para el caso de la mancuerna dado que c < 1, esta percusión de reacción siempre es opuesta a la que aplicamos, pero para la barra homogénea, puede tanto ir en sentido opuesto como en el mismo sentido, dependiendo del punto de aplicación. En particular, si <math>c=b/3</math>, la percusión de reacción es nula. | ||
| + | |||
| + | ==Caso de una barra empotrada== | ||
| + | Si la barra está empotrada, su estado tras percusión es de reposo | ||
| + | |||
| + | <center><math>\vec{v}^{G+}_{21}=\vec{0}\qquad\qquad\vec{\omega}_{21}^+=\vec{0}</math></center> | ||
| + | |||
| + | Esto nos da directamente la percusión de reacción en O | ||
| + | |||
| + | <center><math>\vec{0}=\vec{P}_O+\vec{P}_A\qquad\Rightarrow\qquad \vec{P}_O=-P\vec{\jmath}</math></center> | ||
| + | |||
| + | y el momento impulsivo de reacción | ||
| + | |||
| + | <center><math>\vec{0}=\vec{H}_O+\overrightarrow{OA}\times\vec{P}_A\qquad\Rightarrow\qquad \vec{H}_O=-(c+b)P\vec{k}</math></center> | ||
última version al 00:01 13 ene 2020
Contenido |
1 Enunciado
¿Cómo cambian los resultados del problema “Percusión sobre una mancuerna y una barra” los dos problemas anteriores si la barra está articulada a un punto fijo O, situado en uno de los extremos de la barra? ¿Cuánto valen las percusiones y momentos impulsivos de reacción en O?
¿Y sí en lugar de estar articulada, está empotrada en O?
2 Introducción
A diferencia del problema mencionado, en este existe un vínculo que limita el movimiento de la varilla. La articulación en O hace que el movimiento sea necesariamente una rotación alrededor de este punto. Esto relaciona la velocidad del CM con la velocidad angular
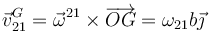
Por su parte, dado que la rotación se produce en torno a O, que e sun punto fijo, interesa el momento de inercia respecto a un eje ortogonal a la varilla por O. Aplicando el teorema de Steiner
siendo γ = 1 para una mancuerna (varilla sin masa, con dos masas en los extremos, en este caso una en la propia articulación) y γ = 1 / 3 para la barra homogénea.
3 Momento cinético respecto a O
El teorema del momento cinético, aplicado en O, nos da
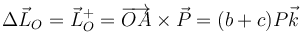
lo que nos da la velocidad angular tras la percusión, por ser un eje principal,
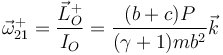
4 Cantidad de movimiento
Una vez que tenemos la velocidad angular, tenemos la del CM
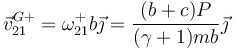
y por tanto la cantidad de movimiento tras la percusión
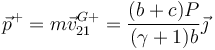
5 Momento cinético respecto al CM
Si queremos el momento cinético respecto al CM podemos trasladarlo mediante la relación
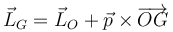
o aplicar directamente
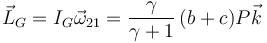
6 Energía cinética
La energía cinética tras la percusión la obtenemos a partir del momento cinético en O
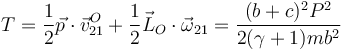
Esta energía cinética es menor que la que se tiene para la barra libre. Esto es una propiedad general, la presencia de vínculos reduce la ganancia de energía cinética.
7 Percusión de reacción
La percusión de reacción la obtenemos que sabemos como ha cambiado la cantidad de movimiento del sistema
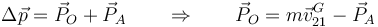
lo que nos da
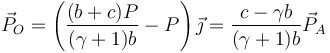
Para el caso de la mancuerna dado que c < 1, esta percusión de reacción siempre es opuesta a la que aplicamos, pero para la barra homogénea, puede tanto ir en sentido opuesto como en el mismo sentido, dependiendo del punto de aplicación. En particular, si c = b / 3, la percusión de reacción es nula.
8 Caso de una barra empotrada
Si la barra está empotrada, su estado tras percusión es de reposo

Esto nos da directamente la percusión de reacción en O
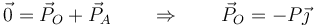
y el momento impulsivo de reacción