Percusión sobre una mancuerna y una barra

De Laplace

Contenido

1 Enunciado
2 Magnitudes tras la percusión
3 Centro instantáneo de rotación
4 Movimiento posterior
5 Caso de una barra

1 Enunciado

Supongamos dos masas iguales $m / 2$ unidas por una barra rígida de longitud $2 b$ , sin masa (lo que sería una mancuerna ideal). Las masas reposan sobre un plano horizontal, sobre el que pueden moverse sin rozamiento. Se comunica una percusión $\vec{P}$ perpendicular a la barra a una distancia $c$ de su centro.

¿Cuánto valen la cantidad de movimiento, el momento cinético respecto al CM y la energía cinética de la barra tras la percusión?
¿Dónde se encuentra el centro instantáneo de rotación justo tras la percusión?
¿Cómo es el movimiento del sistema a partir de ese momento?
¿Cómo cambian los resultados de los apartados anteriores si en lugar de una mancuerna tenemos una barra homogénea de longitud $2 b$ y masa $m$ a la cual se comunica una percusión $\vec{P}$ perpendicular a la barra a una distancia $c$ de su centro?

2 Magnitudes tras la percusión

2.1 Cantidad de movimiento

De acuerdo con el teorema de la cantidad de movimiento para percusiones

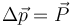
$\Delta \vec{p}=\vec{P}$

Antes de la percusión, la cantidad de movimiento es nula, por lo que

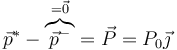
$\vec{p}^*-\overbrace{\vec{p}^-}^{=\vec{0}}=\vec{P}=P_0\vec{\jmath}$

Esto nos da también la velocidad del CM justo tras la percusión

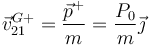
$\vec{v}^{G+}_{21}=\frac{\vec{p}^+}{m}=\frac{P_0}{m}\vec{\jmath}$

2.2 Momento cinético

El teorema del momento cinético para percusiones nos da

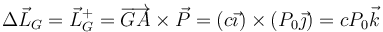
$\Delta \vec{L}_G=\vec{L}^+_G=\overrightarrow{GA}\times \vec{P}=(c\vec{\imath})\times(P_0\vec{\jmath})=cP_0\vec{k}$

El eje perpendicular a la varilla por su centro es un eje principal, siendo su momento de inercia

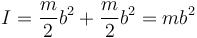
$I=\frac{m}{2}b^2+\frac{m}{2}b^2=mb^2$

por lo que la velocidad angular de la mancuerna tras la percusión es

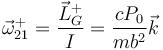
$\vec{\omega}^+_{21}=\frac{\vec{L}_G^+}{I}=\frac{cP_0}{mb^2}\vec{k}$

2.3 Energía cinética

Para un sólido rígido, si tenemos la cantidad de movimiento y el momento cinético, tenemos la energía cinética.

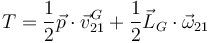
$T=\frac{1}{2}\vec{p}\cdot\vec{v}^G_{21}+\frac{1}{2}\vec{L}_G\cdot\vec{\omega}_{21}$

Antes de la percusión, la energía cinética es nula. Tras ella, vale

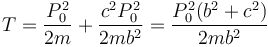
$T=\frac{P_0^2}{2m}+\frac{c^2P_0^2}{2mb^2}=\frac{P_0^2(b^2+c^2)}{2mb^2}$

3 Centro instantáneo de rotación

Conocidas la velocidad del CM y la velocidad angular tenemos la posición del CIR

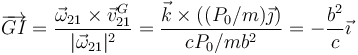
$\overrightarrow{GI}=\frac{\vec{\omega}_{21}\times\vec{v}^G_{21}}{|\vec{\omega}_{21}|^2}=\frac{\vec{k}\times\left((P_0/m)\vec{\jmath}\right)}{cP_0/mb^2}=-\frac{b^2}{c}\vec{\imath}$

La posición de este centro depende de donde se aplique la percusión. Si se aplica en un extremo ( $c = b$ ), el CIR está en el otro extremo. Si se aplica en el centro, el CIR está en el infinito.

4 Movimiento posterior

Si no hay más acciones sobre el sistema tanto la cantidad de movimiento como el momento cinético permanecen constantes. Esto implica que también permanecen constantes la velocidad del CM y la velocidad angular. Por tanto, la posición del CIR respecto al CM permanece constante.

El resultado es que la varilla describe un movimiento equivalente al de una rueda. Si la percusión es el centro simplemente se traslada, mientras que si es en el extremo, cada masa describe un movimiento cicloidal.

5 Caso de una barra

En el caso de que tengamos una barra homogénea en lugar de una mancuerna, lo único que cambia es el momento de inercia, que ahora pasa a ser

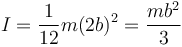
$I=\frac{1}{12}m(2b)^2=\frac{mb^2}{3}$

Esto afecta a la nueva velocidad angular

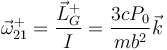
$\vec{\omega}^+_{21}=\frac{\vec{L}_G^+}{I}=\frac{3cP_0}{mb^2}\vec{k}$

a la energía cinética

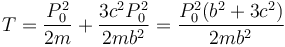
$T=\frac{P_0^2}{2m}+\frac{3c^2P_0^2}{2mb^2}=\frac{P_0^2(b^2+3c^2)}{2mb^2}$

y a la posición del CIR

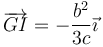
$\overrightarrow{GI}=-\frac{b^2}{3c}\vec{\imath}$

Para una percusión en el extremo de la barra ( $c = b$ ) el CIR se halla en 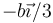$-b\vec{\imath}/3$ , es decir, a 1/6 de los longitud total de la barra medido desde el centro (o 1/3, medido desde el extremo). La curva que describen los extremos es una cicloide alargada.

Percusión sobre una mancuerna y una barra

De Laplace

Contenido

1 Enunciado

2 Magnitudes tras la percusión

2.1 Cantidad de movimiento

2.2 Momento cinético

2.3 Energía cinética

3 Centro instantáneo de rotación

4 Movimiento posterior

5 Caso de una barra

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES