Problemas de dinámica impulsiva (CMR)
De Laplace
(Página creada con '==Percusión en sistema de tres masas== Un sólido está formado por tres masas iguales <math>m</math> unidas por varillas rígidas de la misma longitud, de masa despreciabl…') |
|||
| Línea 1: | Línea 1: | ||
| - | ==[[Percusión en sistema de tres masas | + | ==Percusión sobre una mancuerna== |
| + | Supongamos dos masas iguales <math>m/2</math> unidas por una barra rígida de longitud <math>2b</math>, sin masa (lo que sería una mancuerna ideal). Las masas reposan sobre un plano horizontal, sobre el que pueden moverse sin rozamiento. | ||
| + | Se comunica una percusión <math>\vec{P}</math> perpendicular a la barra a una distancia <math>c</math> de su centro. | ||
| + | # ¿Cuánto valen la cantidad de movimiento, el momento cinético respecto al CM y la energía cinética de la barra tras la percusión? | ||
| + | # ¿Dónde se encuentra el centro instantáneo de rotación justo tras la percusión? | ||
| + | # ¿Cómo es el movimiento del sistema a partir de ese momento? | ||
| + | |||
| + | [[Percusión sobre una mancuerna|Solución]] | ||
| + | |||
| + | ==Percusión en sistema de tres masas== | ||
Un sólido está formado por tres masas iguales <math>m</math> unidas por varillas rígidas de la misma longitud, de masa despreciable. El triángulo se encuentra situado sobre un plano horizontal, sin rozamiento. Se elige un sistema de ejes tal que el baricentro del triángulo es el origen de coordenadas y la masa A se encuentra en <math>b\vec{\imath}</math>, hallándose las masas B y C en las posiciones correspondientes del plano OXY. | Un sólido está formado por tres masas iguales <math>m</math> unidas por varillas rígidas de la misma longitud, de masa despreciable. El triángulo se encuentra situado sobre un plano horizontal, sin rozamiento. Se elige un sistema de ejes tal que el baricentro del triángulo es el origen de coordenadas y la masa A se encuentra en <math>b\vec{\imath}</math>, hallándose las masas B y C en las posiciones correspondientes del plano OXY. | ||
Estando el triángulo en reposo, se golpea la masa A con una percusión <math>\vec{P}=P_0 \vec{\jmath}</math>. Para el instante inmediatamente posterior a la percusión determine (empleando mecánica vectorial o analítica o ambas): | Estando el triángulo en reposo, se golpea la masa A con una percusión <math>\vec{P}=P_0 \vec{\jmath}</math>. Para el instante inmediatamente posterior a la percusión determine (empleando mecánica vectorial o analítica o ambas): | ||
| Línea 9: | Línea 18: | ||
<center>[[Archivo:percusion-tres-masas.png|400px]]</center> | <center>[[Archivo:percusion-tres-masas.png|400px]]</center> | ||
| + | |||
| + | [[Percusión en sistema de tres masas|Solución]] | ||
==[[Percusión sobre una barra. Estudio analítico]]== | ==[[Percusión sobre una barra. Estudio analítico]]== | ||
Revisión de 14:37 12 ene 2020
Contenido |
1 Percusión sobre una mancuerna
Supongamos dos masas iguales m / 2 unidas por una barra rígida de longitud 2b, sin masa (lo que sería una mancuerna ideal). Las masas reposan sobre un plano horizontal, sobre el que pueden moverse sin rozamiento.
Se comunica una percusión  perpendicular a la barra a una distancia c de su centro.
perpendicular a la barra a una distancia c de su centro.
- ¿Cuánto valen la cantidad de movimiento, el momento cinético respecto al CM y la energía cinética de la barra tras la percusión?
- ¿Dónde se encuentra el centro instantáneo de rotación justo tras la percusión?
- ¿Cómo es el movimiento del sistema a partir de ese momento?
2 Percusión en sistema de tres masas
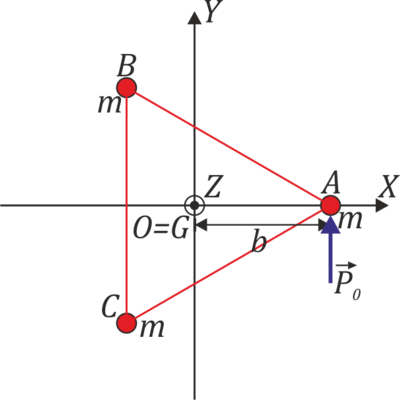
Un sólido está formado por tres masas iguales m unidas por varillas rígidas de la misma longitud, de masa despreciable. El triángulo se encuentra situado sobre un plano horizontal, sin rozamiento. Se elige un sistema de ejes tal que el baricentro del triángulo es el origen de coordenadas y la masa A se encuentra en 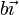 , hallándose las masas B y C en las posiciones correspondientes del plano OXY.
Estando el triángulo en reposo, se golpea la masa A con una percusión
, hallándose las masas B y C en las posiciones correspondientes del plano OXY.
Estando el triángulo en reposo, se golpea la masa A con una percusión 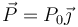 . Para el instante inmediatamente posterior a la percusión determine (empleando mecánica vectorial o analítica o ambas):
. Para el instante inmediatamente posterior a la percusión determine (empleando mecánica vectorial o analítica o ambas):
- La velocidad del centro de masas del triángulo.
- La velocidad angular del triángulo.
- La velocidad de cada una de las masas.
- La posición del centro instantáneo de rotación.
- Calcule los valores de las percusiones de reacción que se producen en las tres varillas en el momento en que se aplica la percusión
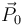 .
.
3 Percusión sobre una barra. Estudio analítico
Suponga una barra homogénea, de masa m y longitud b, situada horizontalmente sobre un plano sin rozamiento.
Estando la barra en reposo, se efectúa sobre ella una percusión 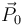 perpendicular a la dirección de la barra y a una distancia c de su centro.
perpendicular a la dirección de la barra y a una distancia c de su centro.
Empleando las técnicas de la mecánica analítica, determine la velocidad del centro de la barra y la velocidad angular de ésta, así como las posibles fuerzas y momentos impulsivos de reacción, en los casos siguientes:
- La barra puede moverse libremente por el plano.
- La barra se halla articulada por un extremo A a una pared inmóvil.
- La barra se halla empotrada por su extremo A a una pared inmóvil.
4 Percusión sobre un sistema articulado
Considerando el sistema de dos barras articuladas del problema “dos barras articuladas” suponga que el sistema se halla completamente extendido y en reposo. Entonces, se efectúa una percusión 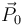 perpendicular a la dirección de las barras y a una distancia c de la articulación A entre las dos barras.
perpendicular a la dirección de las barras y a una distancia c de la articulación A entre las dos barras.
Determine la velocidad angular de cada barra, así como la velocidad de los puntos A y B (extremo libre de la segunda barra) en los casos:
- Se golpea la barra OA en un punto D a una distancia c de la articulación A.
- Se golpea la barra AB en un punto D a una distancia c de la articulación A.





