Test del primer parcial 2019-2020 (GIOI)
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Aceleración a trozos== Una partícula se mueve en un movimiento rectilíneo que parte del reposo en <math>x=0</math>. Durante un intervalo <math>T</math> se mueve con acelera…') |
|||
| Línea 6: | Línea 6: | ||
:* '''B''' <math>a_0 T</math>. | :* '''B''' <math>a_0 T</math>. | ||
:* '''C''' <math>0</math>. | :* '''C''' <math>0</math>. | ||
| - | :* '''D''' <math>a_0 T/2</math> | + | :* '''D''' <math>a_0 T/2</math>. |
;Solución: | ;Solución: | ||
La respuesta correcta es la '''<span style="color:red;">C<span>'''. | La respuesta correcta es la '''<span style="color:red;">C<span>'''. | ||
| Línea 15: | Línea 15: | ||
:* '''B''' <math>3a_0 T^2 /2</math>. | :* '''B''' <math>3a_0 T^2 /2</math>. | ||
:* '''C''' <math>0</math>. | :* '''C''' <math>0</math>. | ||
| - | :* '''D''' <math>-a_0 T^2</math> | + | :* '''D''' <math>-a_0 T^2</math>. |
;Solución: | ;Solución: | ||
La respuesta correcta es la '''<span style="color:red;">B<span>'''. | La respuesta correcta es la '''<span style="color:red;">B<span>'''. | ||
| + | |||
| + | ==Cambio en la velocidad== | ||
| + | En un movimiento en el plano OXY, la velocidad de una partícula en un instante dado es <math>\vec{v}=(-3\vec{\imath}+4\vec{\jmath})\,\mathrm{m}/\mathrm{s}</math> y su aceleración en ese mismo instante es <math>\vec{a}=(7\vec{\imath}-\vec{\jmath} )\,\mathrm{m}/\mathrm{s}^2</math>. | ||
| + | ===Pregunta 1=== | ||
| + | En este instante la partícula está… | ||
| + | :* '''A''' ni frenando ni acelerando. Su rapidez es constante. | ||
| + | :* '''B''' frenando. | ||
| + | :* '''C''' acelerando. | ||
| + | :* '''D''' No hay información suficiente para saber si acelera o frena. | ||
| + | ;Solución: | ||
| + | La respuesta correcta es la '''<span style="color:red;">B<span>'''. | ||
| + | |||
| + | ===Pregunta 2=== | ||
| + | En ese instante y, mirando desde el eje OZ positivo, la partícula… | ||
| + | :* '''A''' está desviándose hacia su izquierda. | ||
| + | :* '''B''' no se desvía, sino que avanza en línea recta. | ||
| + | :* '''C''' está desviándose hacia su derecha. | ||
| + | :* '''D''' No hay información suficiente para saber si cambia de dirección. | ||
| + | ;Solución: | ||
| + | La respuesta correcta es la '''<span style="color:red;">C<span>'''. | ||
| + | |||
| + | ==Producto escalar y vectorial== | ||
| + | Sean <math>\vec{a}</math> y <math>\vec{b}</math> dos vectores no nulos. Indique en qué caso se cumple la igualdad | ||
| + | |||
| + | <center><math>\vec{a}\cdot\vec{b}=\vec{a}\times\vec{b}</math></center> | ||
| + | |||
| + | :* '''A''' Cuando <math>\vec{a}</math> y <math>\vec{b}</math> son paralelos. | ||
| + | :* '''B''' Cuando <math>\vec{a}</math> y <math>\vec{b}</math> son perpendiculares. | ||
| + | :* '''C''' Cuando <math>\vec{a}</math> y <math>\vec{b}</math> forman un ángulo de 45°. | ||
| + | :* '''D''' Nunca. | ||
| + | ;Solución: | ||
| + | La respuesta correcta es la '''<span style="color:red;">D<span>'''. | ||
Revisión de 21:28 5 nov 2019
Contenido |
1 Aceleración a trozos
Una partícula se mueve en un movimiento rectilíneo que parte del reposo en x = 0. Durante un intervalo T se mueve con aceleración constante a0. A partir de ahí se mueve con aceleración constante − a0 / 2 durante un intervalo 2T.
1.1 Pregunta 1
¿Cuánto vale la velocidad de la partícula en t = 3T?
- A − a0T.
- B a0T.
- C 0.
- D a0T / 2.
- Solución
La respuesta correcta es la C.
1.2 Pregunta 2
¿Cuál es el desplazamiento de la partícula entre t = 0 y t = 3T?
- A − 3a0T2 / 2.
- B 3a0T2 / 2.
- C 0.
- D − a0T2.
- Solución
La respuesta correcta es la B.
2 Cambio en la velocidad
En un movimiento en el plano OXY, la velocidad de una partícula en un instante dado es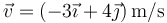 
y su aceleración en ese mismo instante es 
.
2.1 Pregunta 1
En este instante la partícula está…
- A ni frenando ni acelerando. Su rapidez es constante.
- B frenando.
- C acelerando.
- D No hay información suficiente para saber si acelera o frena.
- Solución
La respuesta correcta es la B.
2.2 Pregunta 2
En ese instante y, mirando desde el eje OZ positivo, la partícula…
- A está desviándose hacia su izquierda.
- B no se desvía, sino que avanza en línea recta.
- C está desviándose hacia su derecha.
- D No hay información suficiente para saber si cambia de dirección.
- Solución
La respuesta correcta es la C.
3 Producto escalar y vectorial
Sean 
y 
dos vectores no nulos. Indique en qué caso se cumple la igualdad
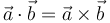
- A Cuando y son paralelos.
- B Cuando y son perpendiculares.
- C Cuando y forman un ángulo de 45°.
- D Nunca.
- A Cuando
- Solución
La respuesta correcta es la D.
