Desplazamiento de un momento
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== El momento del vector <math>\vec{v}=2\vec{\imath}-2\vec{\jmath}+\vec{k}</math> respecto al origen de coordenadas vale <math>\vec{M}_O=8\vec{\imath}+5\vec{\jmath}-6…') |
|||
| Línea 11: | Línea 11: | ||
que en este caso da | que en este caso da | ||
| - | <center><math>\vec{M}_A=8\vec{\imath}+5\vec{\jmath}-6\vec{k}+\left|\begin{matrix}\vec{\imath}&\vec{\jmath}&\vec{k}\\ 2 & -2 & 1 \\ -1 & 4 & 1\right|=2\vec{\imath}+2\vec{\jmath}</math></center> | + | <center><math>\vec{M}_A=8\vec{\imath}+5\vec{\jmath}-6\vec{k}+\left|\begin{matrix}\vec{\imath}&\vec{\jmath}&\vec{k}\\ 2 & -2 & 1 \\ -1 & 4 & 1\end{matrix}\right|=2\vec{\imath}+2\vec{\jmath}</math></center> |
==Recta soporte== | ==Recta soporte== | ||
La recta soporte está formada por los puntos para los cuales el momento es nulo. | La recta soporte está formada por los puntos para los cuales el momento es nulo. | ||
| - | <center><math>\vec{0}=8\vec{\imath}+5\vec{\jmath}-6\vec{k}+\left|\begin{matrix}\vec{\imath}&\vec{\jmath}&\vec{k}\\ 2 & -2 & 1 \\ x & y & z\right|=(8 - y - 2 z)\vec{\imath}+(5 + x - 2 z)\vec{\jmath}+(-6 + 2 x + 2 y)\vec{k}</math></center> | + | <center><math>\vec{0}=8\vec{\imath}+5\vec{\jmath}-6\vec{k}+\left|\begin{matrix}\vec{\imath}&\vec{\jmath}&\vec{k}\\ 2 & -2 & 1 \\ x & y & z\end{matrix}\right|=(8 - y - 2 z)\vec{\imath}+(5 + x - 2 z)\vec{\jmath}+(-6 + 2 x + 2 y)\vec{k}</math></center> |
Separando por componentes y simplificando | Separando por componentes y simplificando | ||
última version al 17:40 7 oct 2019
1 Enunciado
El momento del vector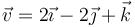 
respecto al origen de coordenadas vale 
.
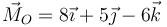- ¿Cuánto vale su momento respecto al punto A(-1,4,1)?
- ¿Cuál es la ecuación de la recta soporte de
?
2 Momento respecto a A
La fórmula para cambiar el centro de reducción de un momento es
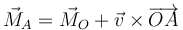
que en este caso da
3 Recta soporte
La recta soporte está formada por los puntos para los cuales el momento es nulo.
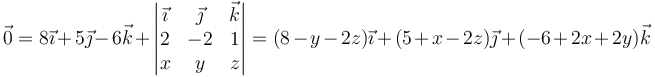
Separando por componentes y simplificando
Estras tres ecuaciones no son todas independientes. Si sumamos las dos primeras, obtenemos la tercera.
En forma paramétrica queda, haciendo z = λ
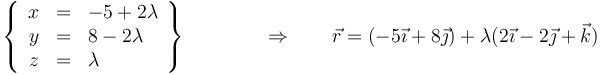
que es la ecuación de la recta que pasa por el punto P(−5,8,0) y lleva la dirección de
