Desplazamiento de un momento

De Laplace

1 Enunciado

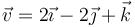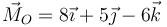El momento del vector $\vec{v}=2\vec{\imath}-2\vec{\jmath}+\vec{k}$ respecto al origen de coordenadas vale $\vec{M}_O=8\vec{\imath}+5\vec{\jmath}-6\vec{k}$ .

¿Cuánto vale su momento respecto al punto A(-1,4,1)?
¿Cuál es la ecuación de la recta soporte de $\vec{v}$ ?

2 Momento respecto a A

La fórmula para cambiar el centro de reducción de un momento es

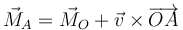
$\vec{M}_A=\vec{M}_O+\vec{v}\times \overrightarrow{OA}$

que en este caso da

$\vec{M}_A=8\vec{\imath}+5\vec{\jmath}-6\vec{k}+\left|\begin{matrix}\vec{\imath}&\vec{\jmath}&\vec{k}\\ 2 & -2 & 1 \\ -1 & 4 & 1\end{matrix}\right|=2\vec{\imath}+2\vec{\jmath}$

3 Recta soporte

La recta soporte está formada por los puntos para los cuales el momento es nulo.

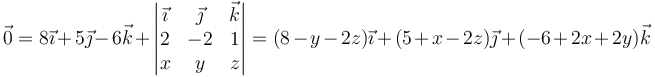
$\vec{0}=8\vec{\imath}+5\vec{\jmath}-6\vec{k}+\left|\begin{matrix}\vec{\imath}&\vec{\jmath}&\vec{k}\\ 2 & -2 & 1 \\ x & y & z\end{matrix}\right|=(8 - y - 2 z)\vec{\imath}+(5 + x - 2 z)\vec{\jmath}+(-6 + 2 x + 2 y)\vec{k}$

Separando por componentes y simplificando

$\left\{\begin{array}{rcl} y+2z&=&8\\ x-2z &=&-5 \\ x+y&=&3\end{array}\right.$

Estras tres ecuaciones no son todas independientes. Si sumamos las dos primeras, obtenemos la tercera.

En forma paramétrica queda, haciendo z = λ

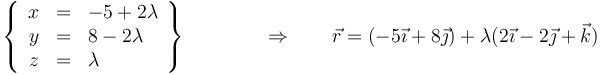
$\left\{\begin{array}{rcl} x&=&-5+2\lambda\\ y&=&8-2\lambda \\ z&=&\lambda\end{array}\right\}\qquad\qquad \Rightarrow\qquad \vec{r}=(-5\vec{\imath}+8\vec{\jmath})+\lambda(2\vec{\imath}-2\vec{\jmath}+\vec{k})$

que es la ecuación de la recta que pasa por el punto P(−5,8,0) y lleva la dirección de $\vec{v}$

Desplazamiento de un momento

De Laplace

1 Enunciado

2 Momento respecto a A

3 Recta soporte

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES