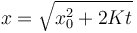Velocidad inversamente proporcional a la posición (GIOI)
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== En un movimiento rectilíneo, la velocidad de una partícula sigue la ley como función de la posición <math>v=K/x</math>. Inicialmente se encuentra en x_0. ¿Qu…') |
(→Solución) |
||
| Línea 16: | Línea 16: | ||
y despejamos | y despejamos | ||
| - | <center><math>x = \sqrt{x_0^2+2Kt</math></center> | + | <center><math>x = \sqrt{x_0^2+2Kt}</math></center> |
Revisión de 15:44 2 oct 2019
1 Enunciado
En un movimiento rectilíneo, la velocidad de una partícula sigue la ley como función de la posición v = K / x. Inicialmente se encuentra en x_0. ¿Qué ley sigue la posición como función del tiempo?
2 Solución
Igualamos la velocidad a su expresión
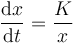
Separamos variables

e integramos
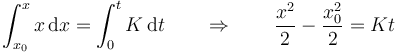
y despejamos