Segunda Convocatoria Ordinaria 2018/19 (G.I.E.R.M.)
De Laplace
(→Tiro parabólico con plano inclinado) |
(→Barra rotando con disco) |
||
| Línea 16: | Línea 16: | ||
==[[ Barra rotando con disco, Septiembre 2019 (G.I.E.R.M.)| Barra rotando con disco ]]== | ==[[ Barra rotando con disco, Septiembre 2019 (G.I.E.R.M.)| Barra rotando con disco ]]== | ||
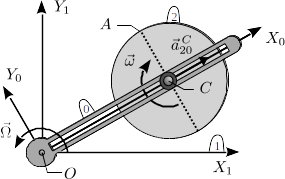
| + | [[File:F1GIERM_barra_disco_enunciado.png|right]] | ||
| + | Una varilla recta y rígida (sólido ``0'') se mueve siempre contenida en el plano | ||
| + | fijo $OX_1Y_1$ (sólido ``1''), girando, con velocidad angular constante $\Omega$ | ||
| + | y en el sentido indicado en la figura, alrededor de su extremo articulado el | ||
| + | punto fijo $O$. El centro $C$ de un disco de radio $R$ (sólido ``2''), recorre | ||
| + | la varilla alejándose con aceleración constante $2a_0$. En el instante inicial | ||
| + | $t=0$, el punto $C$ coincidía con el $O$ y su velocidad era nula. | ||
| + | A su vez, el disco gira | ||
| + | alrededor de su centro $C$ en el sentido indicado, con velocidad angular | ||
| + | constante $\omega$ (respecto a la varilla) y permaneciendo siempre paralelo al | ||
| + | plano fijo $OX_1Y_1$. En el instante inicial la varilla recta | ||
| + | coincidía con el eje $OX_1$, | ||
| + | |||
| + | \parbox{0.5\textwidth}{ | ||
| + | \begin{enumerate} | ||
| + | \item Determina reducciones cinemáticas y sus derivadas temporales de los | ||
| + | movimientos \{01\}, \{20\} y \{21\}. Puedes hacerlo en cualquier punto. | ||
| + | |||
| + | \item En el instante $t=1/\Omega$, encuentra la posición de los C.I.R. de | ||
| + | los tres movimientos. | ||
| + | \end{enumerate} | ||
Revisión de 11:53 25 sep 2019
1 Tiro parabólico con plano inclinado
Se tiene el plano inclinado de la figura que forma un ángulo θ con la horizontal. Se dispara una partícula desde el punto más bajo, con una velocidad inicial  , de módulo 10vp y con un ángulo α con la horizontal. Los ángulos son tales que
, de módulo 10vp y con un ángulo α con la horizontal. Los ángulos son tales que

- Calcula la distancia l entre el punto de partida y el de impacto sobre el plano inclinado, así como la velocidad (vector) con la que impacta.
- Calcula el trabajo realizado por la fuerza gravitatoria sobre la partícula entre los puntos O y A.
- Calcula la potencia que la gravedad transmite a la partícula en cada. Discute el significado físico del signo de esta potencia.
- Calcula las componentes intrínsecas de la aceleración en el punto de impacto.
2 Barra rotando con disco
Una varilla recta y rígida (sólido ``0) se mueve siempre contenida en el plano fijo $OX_1Y_1$ (sólido ``1), girando, con velocidad angular constante $\Omega$ y en el sentido indicado en la figura, alrededor de su extremo articulado el punto fijo $O$. El centro $C$ de un disco de radio $R$ (sólido ``2), recorre la varilla alejándose con aceleración constante $2a_0$. En el instante inicial $t=0$, el punto $C$ coincidía con el $O$ y su velocidad era nula. A su vez, el disco gira alrededor de su centro $C$ en el sentido indicado, con velocidad angular constante $\omega$ (respecto a la varilla) y permaneciendo siempre paralelo al plano fijo $OX_1Y_1$. En el instante inicial la varilla recta coincidía con el eje $OX_1$,
\parbox{0.5\textwidth}{ \begin{enumerate}
\item Determina reducciones cinemáticas y sus derivadas temporales de los
movimientos \{01\}, \{20\} y \{21\}. Puedes hacerlo en cualquier punto.
\item En el instante $t=1/\Omega$, encuentra la posición de los C.I.R. de los tres movimientos.
\end{enumerate}