Test del segundo parcial 2018-2019 (GIE)
De Laplace
(→Clasificación de vínculos) |
|||
| (3 ediciones intermedias no se muestran.) | |||
| Línea 38: | Línea 38: | ||
;Solución: | ;Solución: | ||
La respuesta correcta es la '''<span style="color:red;">D<span>'''. | La respuesta correcta es la '''<span style="color:red;">D<span>'''. | ||
| + | |||
| + | ==Energía potencial== | ||
| + | Una partícula se mueve por el eje OX sometida a una cierta energía potencial <math>U=U(x)</math> como la mostrada en la figura. | ||
| + | |||
| + | <center>[[Archivo:potencial-doble-V.png|400px]]</center> | ||
| + | ¿Dónde se hallan los puntos de retorno de la partícula? | ||
| + | :* '''A''' En x = +2 m y x = +8 m. | ||
| + | :* '''B''' En x = +4 m, en x = +5 m y en x = 6 m | ||
| + | :* '''C''' En x = +3 m, en x = +5 m y en x = 7 m | ||
| + | :* '''D''' Depende de las condiciones iniciales del movimiento. | ||
| + | ;Solución: | ||
| + | La respuesta correcta es la '''<span style="color:red;">D<span>'''. | ||
| + | |||
| + | ==Fuerza dependiente de la posición== | ||
| + | Una partícula de masa m = 2 kg que se puede mover por el eje OX se ve sometida a una fuerza a lo largo del mismo eje dependiente de la posición como | ||
| + | |||
| + | <center><math>F(x)=\begin{cases}0 & (|x|>4\,\mathrm{m}) \\ 4-|x| & (|x|<4\,\mathrm{m})\end{cases}\qquad (x\ \mathrm{en}\ \mathrm{m}, F\ \mathrm{en}\ \mathrm{N})</math></center> | ||
| + | |||
| + | La partícula tiene una velocidad de +3m/s cuando pasa por x = −5 m. ¿Cuál es su velocidad cuando pasa por x = +5 m? | ||
| + | |||
| + | :* '''A''' +5 m/s. | ||
| + | :* '''B''' +3 m/s. | ||
| + | :* '''C''' −3 m/s. | ||
| + | :* '''D''' Nunca llega a ese punto. | ||
| + | |||
| + | ;Solución: | ||
| + | La respuesta correcta es la '''<span style="color:red;">A<span>'''. | ||
| + | |||
| + | ==Clasificación de vínculos== | ||
| + | ¿Cuál de las siguientes no es una clasificación de los tipos de vínculos? | ||
| + | :* '''A''' Esclerónomos y reónomos. | ||
| + | :* '''B''' Bilaterales y unilaterales | ||
| + | :* '''C''' Autónomos y dependientes | ||
| + | :* '''D''' Cinemáticos y geométricos | ||
| + | ;Solución: | ||
| + | La respuesta correcta es la '''<span style="color:red;">C<span>'''. | ||
| + | |||
| + | ==Momento cinético== | ||
| + | Una partícula de masa m se mueve por el plano OXY. ¿Cuál es la expresión en polares de su momento cinético respecto al origen de coordenadas, \vec{L}_O? | ||
| + | :* '''A''' <math>\vec{L}_O=m\rho\dot{\rho}\vec{k}</math> | ||
| + | :* '''B''' <math>\vec{L}_O=m\rho^2 \dot{\theta}\vec{k}</math> | ||
| + | :* '''C''' <math>\vec{L}_O=m(\dot{\rho}\vec{u}_\rho+\rho\dot{\theta}\vec{u}_\theta )</math> | ||
| + | :* '''D''' <math>\vec{L}_O=m(\dot{\rho}^2+\rho^2 \dot{\theta}^2 )/2</math> | ||
| + | ;Solución: | ||
| + | La respuesta correcta es la '''<span style="color:red;">B<span>'''. | ||
última version al 23:52 3 dic 2018
Contenido |
1 Cuerpo en plano inclinado
Un cuerpo de 13 N de peso se encuentra sobre la superficie de un plano inclinado de pendiente tg(β) = 5 / 12. El coeficiente de rozamiento del cuerpo con el plano vale μ=0.5. Desde la parte de abajo del cuerpo se le aplica una fuerza de 9 N, tangente al plano y en sentido ascendente.

¿Cuánto vale, en módulo, la fuerza de rozamiento que experimenta el cuerpo?
- A 6 N.
- B 9 N.
- C 5 N.
- D 4 N.
- Solución
La respuesta correcta es la D.
2 Masa colgando de tres hilos
Una masa de 60 N de peso cuelga suspendida del techo por tres hilos. Uno de ellos es vertical y los otros dos forman un ángulo de 45° con la vertical. Los tres hilos están en el mismo plano vertical.

¿Cuánto vale la tensión de cada uno?
- A
 ,
, 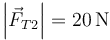 ,
, 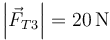 .
.
- B
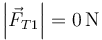 ,
, 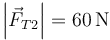 ,
, 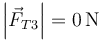 .
.
- C
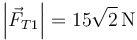 ,
, 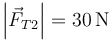 ,
, 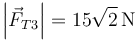 .
.
- D No hay información suficiente para determinarlo.
- A
- Solución
La respuesta correcta es la D.
3 Teorema de König
Sean O un punto fijo y G el centro de masas de un sistema de masa M. ¿Qué establece el teorema de König para el momento cinético?
- A
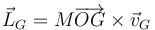
- B
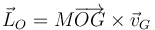
- C

- D
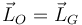
- A
- Solución
La respuesta correcta es la C.
4 Dos masas unidas por un resorte
Dos partículas de masa m se mueven sin rozamiento por un plano horizontal. Las partículas están unidas por un resorte de constante k y longitud natural 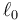 . Estando las dos masas inicialmente en reposo en
. Estando las dos masas inicialmente en reposo en 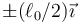 , se le comunica a una de ellas una velocidad inicial
, se le comunica a una de ellas una velocidad inicial  . A partir de ese momento su centro de masas…
. A partir de ese momento su centro de masas…
- A describe un movimiento armónico simple.
- B describe un movimiento circular uniforme.
- C permanece en reposo.
- D describe un movimiento rectilíneo y uniforme.
- Solución
La respuesta correcta es la D.
5 Energía potencial
Una partícula se mueve por el eje OX sometida a una cierta energía potencial U = U(x) como la mostrada en la figura.

¿Dónde se hallan los puntos de retorno de la partícula?
- A En x = +2 m y x = +8 m.
- B En x = +4 m, en x = +5 m y en x = 6 m
- C En x = +3 m, en x = +5 m y en x = 7 m
- D Depende de las condiciones iniciales del movimiento.
- Solución
La respuesta correcta es la D.
6 Fuerza dependiente de la posición
Una partícula de masa m = 2 kg que se puede mover por el eje OX se ve sometida a una fuerza a lo largo del mismo eje dependiente de la posición como
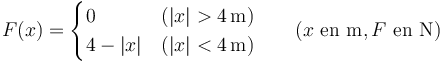
La partícula tiene una velocidad de +3m/s cuando pasa por x = −5 m. ¿Cuál es su velocidad cuando pasa por x = +5 m?
- A +5 m/s.
- B +3 m/s.
- C −3 m/s.
- D Nunca llega a ese punto.
- Solución
La respuesta correcta es la A.
7 Clasificación de vínculos
¿Cuál de las siguientes no es una clasificación de los tipos de vínculos?
- A Esclerónomos y reónomos.
- B Bilaterales y unilaterales
- C Autónomos y dependientes
- D Cinemáticos y geométricos
- Solución
La respuesta correcta es la C.
8 Momento cinético
Una partícula de masa m se mueve por el plano OXY. ¿Cuál es la expresión en polares de su momento cinético respecto al origen de coordenadas, \vec{L}_O?
- A
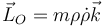
- B
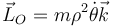
- C
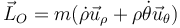
- D
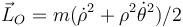
- A
- Solución
La respuesta correcta es la B.





