De Laplace

Revisión de 11:48 3 oct 2018

1 Problemas del boeltín

1.1 Engranaje sobre cremallera

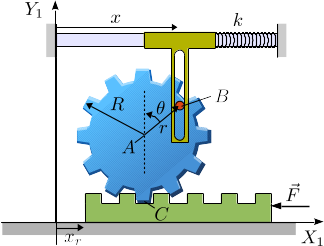
La figura muestra un sistema mecánico formado por un engranaje que rueda sobre una cremallera y está conectado a un deslizador con una ranura que desliza respecto al pasador en B. El deslizador está acoplado a un muelle, de constante elástica k, que se encuentra relajado cuando x = 2R. En ese instante se tiene θ = 0. Las masas del engranaje, el deslizador y la cremallera son la misma e igual a m. El radio de giro del engranaje es r_c. El contacto entre el pasador y la ranura es liso. El mecanismo es accionado por una fuerza aplicada sobe la cremallera como se indica en la figura.

1. Encuentra el número de grados de libertad y elige un conjunto de coordenadas generalizadas para describir el movimiento.
2. Encuentra las ecuaciones diferenciales del movimiento.

1.2 Dos partículas unidas por una barra sin masa con una cuchilla

Dos partículas puntuales de masa m están unidas por una barra de longitud L y masa despreciable. Las partículas deslizan sobre un plano fijo OX₁Y₁, pero una de las partículas tiene una cuchilla, de modo que su velocidad sólo puede tener componente paralela a la cuchilla. Una fuerza 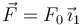constante actúa sobre la partícula que no tiene la cuchilla.

1. Encuentra la expresión del vínculo no holónomo del sistema.
2. Escribe las ecuaciones de Lagrange utilizando la técnica de los multiplicadores de Lagrange.
3. Identifica el significado físico del multiplicador de Lagrange.

2 Otros problemas

2.1 Deslizadera y disco rodando sin deslizar

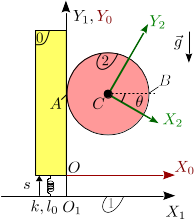
Un disco homogéneo (sólido "2") de masa m y radio R puede rotar alrededor de su centro C, que se mantiene fijo. Una deslizadera vertical (sólido "0"), de masa m puede moverse a lo largo del eje O₁Y₁, de modo que en el punto de contacto A el disco rueda sin deslizar sobre el sólido "0". La deslizadera está conectada a un muelle de constante elástica k y longitud natural l₀. El otro extremo del muelle está anclado en un punto fijo del eje O₁X₁, de modo que se mantiene siempre vertical. El sistema está sometido a la acción de la gravedad como se indica en la figura.

1. ¿Cuantos grados de libertad tiene el sistema? Determina las reducciones cinemáticas de los movimientos {01}, {20} y {21}, así como sus derivadas temporales. El resultado debe quedar en función del número de grados de libertad y sus derivadas temporales.
2. Calcula las energías cinética y potencial del sistema en función de sus grados de libertad.
3. Escribe la lagrangiana del sistema, así como las ecuaciones diferenciales de movimiento.
4. Se aplica sobre el disco un par de fuerzas externo 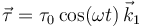. Encuentra las ecuaciones de movimiento en este caso. ¿Para qué valor de ω aparece una resonancia mecánica?
5. Ahora no hay par aplicado. Se aplica una percusión sobre el punto B del sólido "2". En el instante de la percusión se cumple s(0) = l₀, θ(0) = 0, 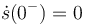, 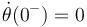. Calcula el estado del sistema inmediatamente después de la percusión.

2.2 Aro colgando de una barra que rota

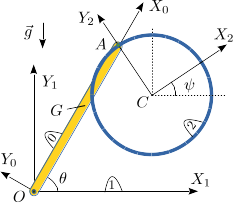
La barra homogénea OA (sólido "0") tiene masa m y longitud L. Está articulada en el punto fijo O y rota de modo que está siempre contenida en el plano OX₁Y₁. En su extremo A está articulado un aro homogéneo de radio R y masa m (sólido "2"). El sistema está sometido a la acción de la gravedad. Se recomienda utilizar los ángulos {θ,ψ} como coordenadas para resolver el problema.

1. Determina las reducciones cinemáticas de los movimientos {01}, {21}, {20}.
2. Calcula las energías cinética y potencial totales del sistema.
3. Usando las herramientas de la Dinámica Analítica, encuentra las ecuaciones de movimiento.
4. Se impone el vínculo cinemático 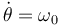. Determina el par necesario para imponer dicho vínculo. Supón que en el instante inicial se tiene θ(0) = 0, ψ(0) = 0.
5. Supongamos que las coordenadas {θ,ψ} son de nuevo libres. Supón que se tiene θ(0) = 0, ψ(0) = 0. En ese instante una percusión actúa sobre el punto A. Determina el estado cinemático del sistema justo después de la percusión.

3 = =Barra rotando alrededor de barra horizontal con muelle

Una barra de longitud 2d y masa despreciable (sólido "0") puede rotar alrededor del eje OZ₁. El punto O de la barra es fijo. La barra "0" siempre está contenida en el plano OX₁Y₁. Otra barra, también de longitud 2d y masa m (sólido "2"), está conectada a la barra "0" por un pasador en el punto A. El pasador desliza sobre la barra "0". Además, la barra "2" gira alrededor de la barra "0". Un muelle de constante elástica k y longitud natural nula l₀ = d conecta los puntos O y A.

1. Determina las reducciones cinemáticas {01},{20} y {21} en G.
2. Calcula el momento cinético de la barra "2" respecto de G.
3. A partir de ahora suponemos que 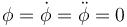, es decir, la coordenada φ ya no es un grado de libertad. Escribe las ecuaciones de Lagrange del sistema.
4. En t = 0 tenemos s(0) = d, θ(0) = − π / 2, 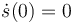y 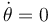(φ sigue estando fijada). La barra "2" recibe una percusión en el punto B. Determina el estado del sistema justo después de la percusión.