De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

Dos partículas puntuales de masa $m$ están unidas por una barra de longitud $L$ y masa despreciable. Las partículas deslizan sobre un plano fijo $O X 1 Y 1$ , pero una de las partículas tiene una cuchilla, de modo que su velocidad sólo puede tener componente paralela a la cuchilla. Una fuerza 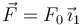$\vec{F}=F_0\,\vec{\imath}_1$ constante actúa sobre la partícula que no tiene la cuchilla.

Encuentra la expresión del vínculo no holónomo del sistema.
Escribe las ecuaciones de Lagrange utilizando la técnica de los multiplicadores de Lagrange.
Identifica el significado físico del multiplicador de Lagrange.

2 Solución

2.1 Cinemática y vínculo

La reducción cinemática del sólido en el punto $A$ es

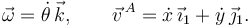
$\vec{\omega} = \dot{\theta}\,\vec{k}, \qquad \vec{v}^{\,A} = \dot{x}\,\vec{\imath}_1 + \dot{y}\,\vec{\jmath}_1.$

La cuchilla hace que la velocidad del punto $A$ tenga que ser paralela a la propia barra. Tenemos

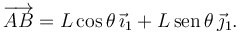
$\overrightarrow{AB} = L\cos\theta\,\vec{\imath}_1 + L\,\mathrm{sen}\,\theta\,\vec{\jmath}_1.$

La ligadura es

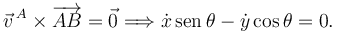
$\vec{v}^{\,A}\times\overrightarrow{AB}=\vec{0} \Longrightarrow \dot{x}\,\mathrm{sen}\,\theta - \dot{y}\cos\theta = 0.$

Esta es una ligadura cinemática no holónoma.

2.2 Ecuaciones de Lagrange

El sistema tiene tres grados de libertad, pero al ser una ligadura no holónoma, trabajaremos con tres coordenadas: ${x, y,θ}$ . La ligadura no holónoma obliga a introducir un multiplicador de Lagrange.

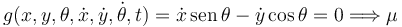
$g(x,y,\theta,\dot{x}, \dot{y}, \dot{\theta}, t) = \dot{x}\,\mathrm{sen}\,\theta - \dot{y}\cos\theta = 0 \Longrightarrow \mu$

Las tres ecuaciones de Lagrange son

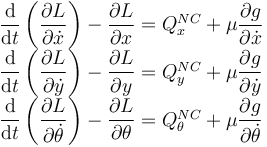
$\begin{array}{l} \dfrac{\mathrm{d}}{\mathrm{d}t}\left(\dfrac{\partial L}{\partial \dot{x}}\right) - \dfrac{\partial L}{\partial x} = Q^{NC}_x + \mu\dfrac{\partial g}{\partial\dot{x}}\\ \dfrac{\mathrm{d}}{\mathrm{d}t}\left(\dfrac{\partial L}{\partial \dot{y}}\right) - \dfrac{\partial L}{\partial y} = Q^{NC}_y + \mu\dfrac{\partial g}{\partial\dot{y}}\\ \dfrac{\mathrm{d}}{\mathrm{d}t}\left(\dfrac{\partial L}{\partial \dot{\theta}}\right) - \dfrac{\partial L}{\partial \theta} = Q^{NC}_\theta + \mu\dfrac{\partial g}{\partial\dot{\theta}} \end{array}$

La energía cinética es la suma de la energía cinética de las dos masas

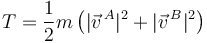
$T = \dfrac{1}{2}m\left(|\vec{v}^{\,A}|^2 + |\vec{v}^{\,B}|^2\right)$

Usando el Teorema de Chasles

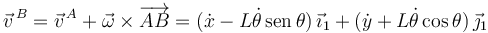
$\vec{v}^{\,B} = \vec{v}^{\,A} + \vec{\omega}\times\overrightarrow{AB} = (\dot{x} - L\dot{\theta}\,\mathrm{sen}\,\theta)\,\vec{\imath}_1 + (\dot{y} + L\dot{\theta}\cos\theta)\,\vec{\jmath}_1$

Por tanto

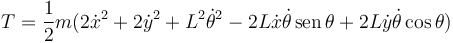
$T = \dfrac{1}{2}m(2\dot{x}^2 + 2\dot{y}^2 + L^2\dot{\theta}^2 - 2L\dot{x}\dot{\theta}\,\mathrm{sen}\,\theta + 2L\dot{y}\dot{\theta}\cos\theta)$

La altura de las bolas no cambian, por lo que la energía potencial gravitatoria es constante y no hace falta considerarla. Así pues, la función Lagrangiana es

$L = T = \dfrac{1}{2}m(2\dot{x}^2 + 2\dot{y}^2 + L^2\dot{\theta}^2 - 2L\dot{x}\dot{\theta}\,\mathrm{sen}\,\theta + 2L\dot{y}\dot{\theta}\cos\theta)$

2.2.1 Ecuación para $x$

Tenemos

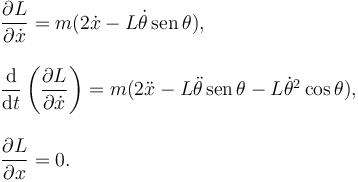
$\begin{array}{l} \dfrac{\partial L}{\partial \dot{x}} = m(2\dot{x} - L\dot{\theta}\,\mathrm{sen}\,\theta), \\ \\ \dfrac{\mathrm{d}}{\mathrm{d}t}\left(\dfrac{\partial L}{\partial \dot{x}}\right) = m(2\ddot{x} - L\ddot{\theta}\,\mathrm{sen}\,\theta -L\dot{\theta}^2\cos\theta), \\ \\ \dfrac{\partial L}{\partial x} = 0. \end{array}$

La contribución de la fuerza no conservativa es

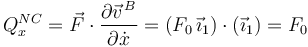
$Q^{NC}_x = \vec{F}\cdot\dfrac{\partial \vec{v}^{\,B}}{\partial \dot{x}} = (F_0\,\vec{\imath}_1)\cdot(\vec{\imath}_1) = F_0$

Y la del multiplicador de Lagrange

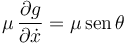
$\mu\,\dfrac{\partial g}{\partial\dot{x}} = \mu\,\mathrm{sen}\,\theta$

La ecuación es

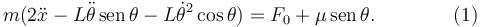
$m(2\ddot{x} - L\ddot{\theta}\,\mathrm{sen}\,\theta -L\dot{\theta}^2\cos\theta) = F_0 + \mu\,\mathrm{sen}\,\theta. \qquad\qquad (1)$

2.2.2 Ecuación para $y$

Tenemos

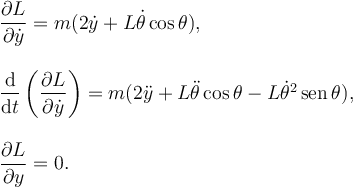
$\begin{array}{l} \dfrac{\partial L}{\partial \dot{y}} = m(2\dot{y} + L\dot{\theta}\cos\theta), \\ \\ \dfrac{\mathrm{d}}{\mathrm{d}t}\left(\dfrac{\partial L}{\partial \dot{y}}\right) = m(2\ddot{y} + L\ddot{\theta}\cos\theta -L\dot{\theta}^2\,\mathrm{sen}\,\theta), \\ \\ \dfrac{\partial L}{\partial y} = 0. \end{array}$

La contribución de la fuerza no conservativa es

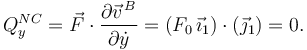
$Q^{NC}_y = \vec{F}\cdot\dfrac{\partial \vec{v}^{\,B}}{\partial \dot{y}} = (F_0\,\vec{\imath}_1)\cdot(\vec{\jmath}_1) = 0.$

Y la del multiplicador de Lagrange

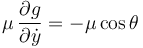
$\mu\,\dfrac{\partial g}{\partial\dot{y}} = -\mu\cos\theta$

La ecuación es

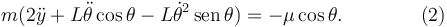
$m(2\ddot{y} + L\ddot{\theta}\cos\theta -L\dot{\theta}^2\,\mathrm{sen}\,\theta) = -\mu\cos\theta. \qquad \qquad (2)$

2.2.3 Ecuación para $θ$

Tenemos

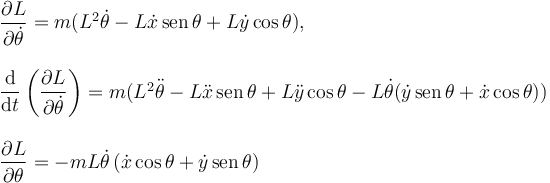
$\begin{array}{l} \dfrac{\partial L}{\partial \dot{\theta}} = m(L^2\dot{\theta} - L\dot{x}\,\mathrm{sen}\,\theta + L\dot{y}\cos\theta), \\ \\ \dfrac{\mathrm{d}}{\mathrm{d}t}\left(\dfrac{\partial L}{\partial \dot{\theta}}\right) = m(L^2\ddot{\theta} - L\ddot{x}\,\mathrm{sen}\,\theta + L\ddot{y}\cos\theta - L\dot{\theta}(\dot{y}\,\mathrm{sen}\,\theta + \dot{x}\cos\theta)) \\ \\ \dfrac{\partial L}{\partial \theta} = -mL\dot{\theta}\,(\dot{x}\cos\theta + \dot{y}\,\mathrm{sen}\,\theta) \end{array}$

La contribución de la fuerza no conservativa es

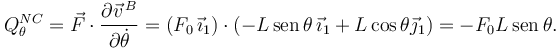
$Q^{NC}_{\theta} = \vec{F}\cdot\dfrac{\partial \vec{v}^{\,B}}{\partial \dot{\theta}} = (F_0\,\vec{\imath}_1)\cdot(-L\,\mathrm{sen}\,\theta\,\vec{\imath}_1 + L\cos\theta\vec{\jmath}_1) = -F_0L\,\mathrm{sen}\,\theta.$

Y la del multiplicador de Lagrange

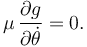
$\mu\,\dfrac{\partial g}{\partial\dot{\theta}} = 0.$

La ecuación es

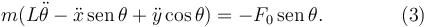
$m(L\ddot{\theta} - \ddot{x}\,\mathrm{sen}\,\theta + \ddot{y}\cos\theta) = -F_0\,\mathrm{sen}\,\theta. \qquad\qquad (3)$

La cuarta ecuación es el propio vínculo

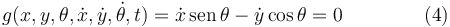
$g(x,y,\theta,\dot{x}, \dot{y}, \dot{\theta}, t) = \dot{x}\,\mathrm{sen}\,\theta - \dot{y}\cos\theta = 0\,\qquad\qquad (4)$

Tenemos 4 incógnitas: ${x, y,θ,μ}$ y 4 ecuaciones.

2.3 Significado físico del multiplicador

Si aplicásemos el Principio de Liberación, al liberar el vínculo sobre la partícula $A$ tendríamos que incluir una fuerza vincular sobre ella perpendicular a la barra, pues ese es el movimiento prohibido de la partícula

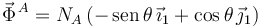
$\vec{\Phi}^{\,A} = N_A\,(-\,\mathrm{sen}\,\theta\,\vec{\imath}_1 + \cos\theta\,\vec{\jmath}_1)$

La contribución de esta fuerza vincular a las diferentes componentes de fuerza generalizada serían

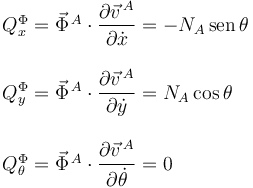
$\begin{array}{l} Q^{\Phi}_{x} = \vec{\Phi}^{\,A}\cdot\dfrac{\partial\vec{v}^{\,A}}{\partial\dot{x}} = -N_A\,\mathrm{sen}\,\theta\\ \\ Q^{\Phi}_{y} = \vec{\Phi}^{\,A}\cdot\dfrac{\partial\vec{v}^{\,A}}{\partial\dot{y}} = N_A\cos\theta\\ \\ Q^{\Phi}_{\theta} = \vec{\Phi}^{\,A}\cdot\dfrac{\partial\vec{v}^{\,A}}{\partial\dot{\theta}} = 0 \end{array}$

Comparando con las contribuciones del multiplicador de Lagrange vemos que

$μ = - N A .$

Dos partículas unidas por una barra sin masa con una cuchilla, (MR)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Cinemática y vínculo

2.2 Ecuaciones de Lagrange

2.2.1 Ecuación para $x$

2.2.2 Ecuación para $y$

2.2.3 Ecuación para $θ$

2.3 Significado físico del multiplicador

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

Dos partículas unidas por una barra sin masa con una cuchilla, (MR)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Cinemática y vínculo

2.2 Ecuaciones de Lagrange

2.2.1 Ecuación para x

2.2.2 Ecuación para y

2.2.3 Ecuación para θ

2.3 Significado físico del multiplicador

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

2.2.1 Ecuación para $x$

2.2.2 Ecuación para $y$

2.2.3 Ecuación para $θ$