Partícula con velocidad dependiente de x
De Laplace
(Diferencias entre revisiones)
(Página creada con '= Enunciado = ==Partícula con velocidad dependiente de x== Una partícula se desplaza sobre el eje <math>OX</math> de modo que su velocidad cumple en cada instante <math>v(…') |
(→Solución) |
||
| Línea 21: | Línea 21: | ||
\int \dfrac{\mathrm{d}x}{x} = A\int\mathrm{d}t | \int \dfrac{\mathrm{d}x}{x} = A\int\mathrm{d}t | ||
\Longrightarrow | \Longrightarrow | ||
| - | \ln x = | + | \ln x = At + C |
</math> | </math> | ||
</center> | </center> | ||
última version al 17:34 26 sep 2018
1 Enunciado
1.1 Partícula con velocidad dependiente de x
Una partícula se desplaza sobre el eje OX de modo que su velocidad cumple en cada instante v(x) = Ax, siendo A una constante. En el instante inicial la coordenada de la partícula es x0. Determina la función x(t).
2 Solución
La velocidad de una partícula en el movimiento rectilíneo es

Podemos integrar esta ecuación diferencial
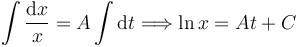
Imponemos la condición inicial
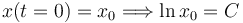
Operando llegamos a






