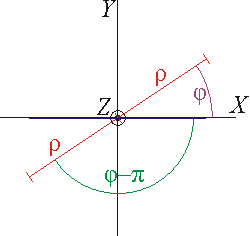Coordenadas cilíndricas. Definición
De Laplace
(Nueva página: Imagen:cil-def.png Las coordenadas cilíndricas constituyen una generalización de las coordenadas polares del plano, a base de extenderlas al espacio paralelamente a una recta (e...) |
(→Enlaces) |
||
| (24 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| - | [[Imagen:cil-def.png]] Las coordenadas cilíndricas constituyen una | + | ==Definición== |
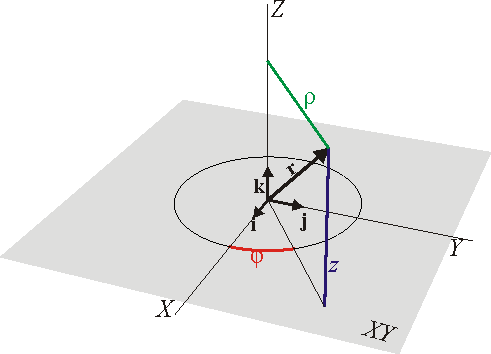
| - | generalización de las coordenadas polares del plano, a base de | + | [[Imagen:cil-def.png|right]] Las coordenadas cilíndricas constituyen una generalización de las coordenadas polares del plano, a base de extenderlas al espacio paralelamente a una recta (el eje <math>Z\,</math>), perpendicular al plano <math>XY\,</math>, como sigue: |
| - | extenderlas al espacio paralelamente a una recta (el eje <math>Z</math>), | + | |
| - | perpendicular al plano <math>XY</math>, como sigue: | + | |
| - | * La coordenada ''radial'', <math>\rho</math>, es la distancia (en valor | + | * La coordenada ''radial'', <math>\rho\,</math>, es la distancia (en valor absoluto) del punto <math>P\,</math> al eje <math>Z\,</math>. |
| - | absoluto) del punto <math>P</math> al eje <math>Z</math>. | + | * La coordenada ''acimutal'', <math>\varphi\,</math>, es el ángulo que la proyección del vector de posición sobre el plano <math>XY\,</math> forma con el eje <math>X\,</math>. |
| - | * La coordenada ''acimutal'', <math>\varphi | + | * La coordenada vertical, <math>z\,</math>, es la distancia (con signo) al plano <math>XY\,</math>. |
| - | proyección del vector de posición sobre el plano <math>XY</math> forma con el eje | + | |
| - | <math>X</math>. | + | |
| - | * La coordenada vertical, <math>z</math>, es la distancia (con signo) al plano | + | |
| - | <math>XY</math>. | + | |
Los rangos de variación de estas coordenadas son: | Los rangos de variación de estas coordenadas son: | ||
| Línea 16: | Línea 10: | ||
<math>\rho\in [0,\infty)\qquad {\varphi} \in (-\pi,\pi]\qquad z\in (-\infty,\infty)</math> | <math>\rho\in [0,\infty)\qquad {\varphi} \in (-\pi,\pi]\qquad z\in (-\infty,\infty)</math> | ||
| - | El ángulo <math>\varphi | + | El ángulo <math>\varphi</math> también puede variar en el intervalo <math>[0,2\pi)</math>. |
| - | === | + | ===<math>\rho</math> es siempre una cantidad positiva=== |
| - | [[Imagen: | + | [[Imagen:cruceeje.png|left]] |
| - | + | A diferencia de las distancias en cartesianas, que tienen un signo indicando a qué lado del plano se encuentran, la coordenada radial cilíndrica es siempre positiva. | |
| - | se | + | |
| - | + | ||
| - | + | ||
| - | + | Si nos encontramos en un punto y, sin cambiar <math>z\,</math> ni <math>\varphi</math>, vamos reduciendo <math>\rho</math> lo que hacemos es acercarnos al eje <math>Z\,</math> en línea recta. ¿Qué ocurre cuando atravesamos el eje? Que a partir de ahí <math>\rho\,</math> vuelve a aumentar, pero <math>\varphi\,</math> cambia a <math>\varphi+\pi</math> o a <math>\varphi-\pi</math>. | |
| - | + | ||
| - | de | + | |
| - | + | ||
| - | + | ===Discos duros=== | |
| - | + | ||
| - | + | ||
| - | + | ||
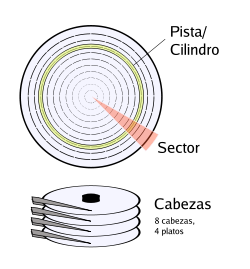
| - | + | [[Imagen:hd.png|right]] | |
| - | + | La ubicación de los datos en los discos duros mediante el sistema CHS se realiza indicando tres cantidades: el cilindro (C), la cabeza (H) y el sector (S). Para ver qué tiene que ver esto con las coordenadas cilíndricas conviene describir cómo son los discos duros. | |
| - | + | ||
| - | + | ||
| - | + | Un disco duro en realidad es una pila de discos (por ejemplo, 4 discos) separados una distancia fija y grabados por sus dos caras. A cada lado de cada disco hay una ''cabeza'' lectora/escritora identificado por el número H, que equivale a la coordenada cilíndrica <math>z\,</math>. | |
| - | + | La distancia al eje de cada disco la da el número C, ya que un ''cilindro'' lo constituyen los puntos a la misma distancia del eje, en los distintos discos. Por tanto, C equivale a la coordenada radial <math>\rho\,</math>. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | Por último, dados la cabeza y el cilindro, la posición a lo largo de una circunferencia (lo que se denomina una ''pista'') se indica | |
| - | + | mediante el ''sector'' S, que corresponde a la coordenada cilíndrica <math>\varphi</math>. | |
| - | + | ||
| - | + | ||
===Grúas=== | ===Grúas=== | ||
| - | [[Imagen:grua.jpg| | + | [[Imagen:grua.jpg|left|frame]]Uno de los ejemplos más sencillos de uso de las coordenadas cilíndricas lo proporcionan las grúas. Para controlar la posición de la carga, es preciso indicar el ángulo de giro de la ''flecha'' (el brazo de la grúa), dado por <math>\varphi</math>, la altura a la que se sube la carga (<math>z\,</math>), y cuanto hay que desplazarla a lo largo de la flecha (<math>\rho\,</math>). |
| + | |||
| + | ==Enlaces== | ||
| + | * '''Siguiente:''' [[Coordenadas esféricas. Definición]] | ||
| + | * '''Anterior:''' [[Coordenadas cartesianas. Definición]] | ||
| + | * [[Coordenadas cilíndricas. Líneas y superficies coordenadas]] | ||
| + | * [[Coordenadas cilíndricas. Base vectorial]] | ||
| + | |||
| + | [[Categoría:Definición de sistemas|30]] | ||
| + | [[Categoría:Coordenadas cilíndricas|10]] | ||
última version al 11:15 23 nov 2007
Contenido |
1 Definición
Las coordenadas cilíndricas constituyen una generalización de las coordenadas polares del plano, a base de extenderlas al espacio paralelamente a una recta (el eje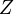 ), perpendicular al plano
), perpendicular al plano 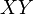 , como sigue:
, como sigue:
- La coordenada radial,
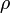 , es la distancia (en valor absoluto) del punto
, es la distancia (en valor absoluto) del punto  al eje
al eje 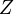 .
.
- La coordenada acimutal,
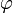 , es el ángulo que la proyección del vector de posición sobre el plano
, es el ángulo que la proyección del vector de posición sobre el plano 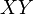 forma con el eje
forma con el eje 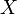 .
.
- La coordenada vertical,
 , es la distancia (con signo) al plano
, es la distancia (con signo) al plano 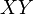 .
.
Los rangos de variación de estas coordenadas son:
![\rho\in [0,\infty)\qquad {\varphi} \in (-\pi,\pi]\qquad z\in (-\infty,\infty)](/wiki/images/math/d/6/0/d60f4eb3686e015c210b89d2f44fd0ec.png)
El ángulo  también puede variar en el intervalo [0,2π).
también puede variar en el intervalo [0,2π).
1.1 ρ es siempre una cantidad positiva
A diferencia de las distancias en cartesianas, que tienen un signo indicando a qué lado del plano se encuentran, la coordenada radial cilíndrica es siempre positiva.
Si nos encontramos en un punto y, sin cambiar  ni
ni  , vamos reduciendo ρ lo que hacemos es acercarnos al eje
, vamos reduciendo ρ lo que hacemos es acercarnos al eje 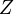 en línea recta. ¿Qué ocurre cuando atravesamos el eje? Que a partir de ahí
en línea recta. ¿Qué ocurre cuando atravesamos el eje? Que a partir de ahí 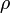 vuelve a aumentar, pero
vuelve a aumentar, pero 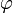 cambia a
cambia a 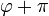 o a
o a 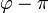 .
.
1.2 Discos duros
La ubicación de los datos en los discos duros mediante el sistema CHS se realiza indicando tres cantidades: el cilindro (C), la cabeza (H) y el sector (S). Para ver qué tiene que ver esto con las coordenadas cilíndricas conviene describir cómo son los discos duros.
Un disco duro en realidad es una pila de discos (por ejemplo, 4 discos) separados una distancia fija y grabados por sus dos caras. A cada lado de cada disco hay una cabeza lectora/escritora identificado por el número H, que equivale a la coordenada cilíndrica  .
.
La distancia al eje de cada disco la da el número C, ya que un cilindro lo constituyen los puntos a la misma distancia del eje, en los distintos discos. Por tanto, C equivale a la coordenada radial 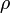 .
.
Por último, dados la cabeza y el cilindro, la posición a lo largo de una circunferencia (lo que se denomina una pista) se indica
mediante el sector S, que corresponde a la coordenada cilíndrica  .
.
1.3 Grúas
Uno de los ejemplos más sencillos de uso de las coordenadas cilíndricas lo proporcionan las grúas. Para controlar la posición de la carga, es preciso indicar el ángulo de giro de la flecha (el brazo de la grúa), dado por , la altura a la que se sube la carga (
, la altura a la que se sube la carga ( ), y cuanto hay que desplazarla a lo largo de la flecha (
), y cuanto hay que desplazarla a lo largo de la flecha (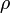 ).
).