Primera Convocatoria Ordinaria 2017/18 (F1 G.I.A.)

De Laplace

Revisión de 20:24 19 ago 2018 (ver código fuente) Gabriel (Discusión | contribuciones) (→Partícula en movimiento con trayectoria y ley horaria conocidas) ← Edición más antigua		Revisión de 12:04 20 ago 2018 (ver código fuente) Gabriel (Discusión | contribuciones) (→Partícula en movimiento con trayectoria y ley horaria conocidas) Edición más nueva →
Línea 11:		Línea 11:
	Obtenga las expresiones de las componentes intrínsecas y cartesianas de la velocidad y la aceleración, en función del tiempo. Obtenga también la ley horaria <math>\displaystyle s(t)</math> para el parámetro arco.		Obtenga las expresiones de las componentes intrínsecas y cartesianas de la velocidad y la aceleración, en función del tiempo. Obtenga también la ley horaria <math>\displaystyle s(t)</math> para el parámetro arco.
		+
		+	==[[Fuerzas de interacción y aceleraciones en sistema de tres partículas, F1 GIA (Ene, 2018)|Interacciones y aceleraciones en sistema de tres partículas]]==
		+	[[Archivo:f1_gIA_ex1ac_17_18_e2_0.png|right]]Tres partículas <math>P_O</math>, <math>P_1</math> y <math>P_2</math>, de masas conocidas con valores <math>m_0</math>, <math>m_1</math> y <math>m_2</math>, respectivamente, interaccionan entre sí de manera que la fuerza <math>\vec{F}_{ij}</math> que la partícula <math>P_j</math> ejerce sobre la <math>P_i</math>, tiene la dirección del segmento <math>\overrightarrow{P_jP_i}</math> (es decir, <math>\vec{F}_{ij}\parallel\pm\overrightarrow{P_jP_i}</math>). En un determinado instante, las partículas ocupan los vértices de un triángulo equilátero; se adopta un sistema de referencia cartesiano <math>OXYZ</math> tal que dicho triángulo está contenido en plano <math>OXY</math>, con el segmento <math>\overrightarrow{P_2P_1}</math> paralelo al eje <math>OX</math>, y la partícula <math>P_0</math> en el punto <math>O</math>. En dicho instante, las aceleraciones de las partículas <math>P_1</math> y <math>P_2</math> tiene igual dirección y sentido, siendo paralelas y opuestas al eje <math>OY</math>; es decir <math>\vec{a}_1=-a_1\!\ \vec{\jmath}\ </math> y <math>\ \vec{a}_2=-a_2\!\ \vec{\jmath}</math>, respectivamente, con <math>a_1\mathrm{,}\, a_2>0</math>
	==[[Cuerpo puntual sobre rampa con rozamiento y resorte, F1 GIA (Ene, 2018)|Cuerpo puntual sobre rampa con rozamiento y resorte]]==		==[[Cuerpo puntual sobre rampa con rozamiento y resorte, F1 GIA (Ene, 2018)|Cuerpo puntual sobre rampa con rozamiento y resorte]]==

---

Revisión de 12:04 20 ago 2018

1 Partícula en movimiento con trayectoria y ley horaria conocidas

Una partícula P se mueve respecto de un sistema de referencia cartesiano OXYZ, recorriendo la curva Γ descrita por la ecuación paramétrica:

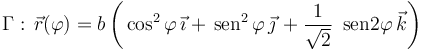
El movimiento de la partícula tiene lugar en el intervalo 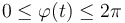, según la ley horaria 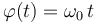. Los parámetros b y ω₀ tienen valores constantes conocidos.

Obtenga las expresiones de las componentes intrínsecas y cartesianas de la velocidad y la aceleración, en función del tiempo. Obtenga también la ley horaria 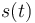para el parámetro arco.

2 Interacciones y aceleraciones en sistema de tres partículas

Tres partículas P_O, P₁ y P₂, de masas conocidas con valores m₀, m₁ y m₂, respectivamente, interaccionan entre sí de manera que la fuerza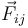 que la partícula P_j ejerce sobre la P_i, tiene la dirección del segmento 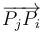(es decir, 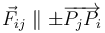). En un determinado instante, las partículas ocupan los vértices de un triángulo equilátero; se adopta un sistema de referencia cartesiano OXYZ tal que dicho triángulo está contenido en plano OXY, con el segmento 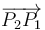paralelo al eje OX, y la partícula P₀ en el punto O. En dicho instante, las aceleraciones de las partículas P₁ y P₂ tiene igual dirección y sentido, siendo paralelas y opuestas al eje OY; es decir 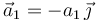y 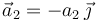, respectivamente, con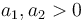

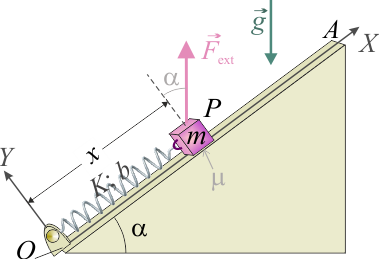
3 Cuerpo puntual sobre rampa con rozamiento y resorte

Un cuerpo que puede ser considerado como un punto material P de masa m, se encuentra en una rampa estrecha OA que forma con la horizontal un ángulo α tal que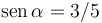 y 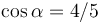. Entre partícula y rampa se establece un contacto unilateral; además, el contacto es rugoso, estando caracterizado por un coeficiente de rozamiento seco, que aproximadamente tiene el mismo valor, tanto para el caso estático como para el dinámico

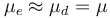. Un resorte de longitud natural b y constante recuperadora K conecta la partícula P con el extremo fijo de la rampa, O. Se sugiere utilizar un sistema de referencia cartesiano en que la rampa coincide con el eje OX y el eje OY es perpendicular a la superficie Σ de la misma. Los parámetros del sistema presentan valores tales que verifican la relación .

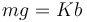1. Obtenga la posición de la rampa en que la partícula se mantendría en equilibrio, P_eq = P(x_eq,0), en el caso en que no hubiese rozamiento (μ = 0). Calcule el valor de la reacción normal del plano-rampa sobre la partícula.
2. Analice el equilibrio del sistema en el caso de que exista rozamiento (), y obtenga la expresión algebraica que permite determinar el rango de posiciones de equilibrio de la partícula en la rampa. ¿Cuál es dicho rango para el caso μ = 1 / 2?
3. Estando la partícula en el punto O, se aplica una fuerza , que en todo momento tiene la dirección y sentido opuesto al peso de la partícula para que ésta ascienda por la rampa; es decir, . ¿Cómo deber ser F(x) para que la partícula se desplace a lo largo de la rampa con velocidad constante? ¿Cuál debe ser su valor máximo para que la partícula no pierda el contacto con la rampa?
4. Calcule el trabajo realizado por la fuerza para llevar la partícula desde O hasta el punto P₀ = P(x₀,0) en que pierde el contacto con la rampa. ¿Y qué trabajo ha realizado la fuerza de rozamiento en el proceso?