Ley de Gauss (GIE)
De Laplace
(Página creada con ' ==Ley de Gauss== Una propiedad del campo eléctrico que se desprende del trazado de sus líneas de campo es la siguiente. Consideremos, por ejemplo, el caso de cuatro cargas i…') |
(→Simetría esférica) |
||
| (39 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| + | |||
| + | ==Flujo de un campo vectorial== | ||
| + | Un concepto básico en electromagnetismo y en mecánica de fluidos es el de ''flujo''. La idea es sencilla: el flujo de un campo vectorial es una medida de “cuánto campo” atraviesa una superficie cerrada. | ||
| + | |||
| + | [[Archivo:flujo-recto.png|right]] | ||
| + | |||
| + | Para definir con precisión lo que se entiende por “cuánto campo”, consideremos en primer lugar el ejemplo sencillo de una tubería por la que fluye agua de manera constante. Queremos saber cuánta agua sale por una boca que es un corte transversal de la tubería. En este caso el caudal, el volumen de agua que pasa en un intervalo <math>\mathrm{d}t</math> es la contenida en una porción de tubería adyacente al orificio de salida | ||
| + | |||
| + | <center><math>\mathrm{d}V = S\,\mathrm{d}x</math></center> | ||
| + | |||
| + | la longitud de la porción corresponde a la que le da tiempo a llegar a la salida en <math>\mathrm{d}t</math> | ||
| + | |||
| + | <center><math>\mathrm{d}x=v\,\mathrm{d}t</math></center> | ||
| + | |||
| + | de forma que el caudal es igual a | ||
| + | |||
| + | <center><math>\dot{V}=\frac{\mathrm{d}V}{\mathrm{d}t}=\Phi =v S\,</math></center> | ||
| + | |||
| + | La cantidad de agua es mayor cuanto más rápido se mueva el agua y cuando mayor sea la sección de la tubería. | ||
| + | |||
| + | [[Archivo:flujo-oblicuo.png|right]] | ||
| + | |||
| + | Supongamos ahora que la boca de la tubería no es transversal sino oblicua. No podemos seguir usando la expresión anterior, ya que ahora la sección tiene mayor área, pero la cantidad de agua que sale por la boca del tubo debería ser la misma que antes. La corrección que hay que hacer viene de que el vector velocidad puede descomponerse en dos partes, una perpendicular a la superficie y una tangencial a ella. Sólo la componente normal atraviesa la superficie. La tangencial “resbala” sobre ella. Por tanto, debemos escribir el flujo como | ||
| + | |||
| + | <center><math>\Phi = v_n\,S</math></center> | ||
| + | |||
| + | En forma vectorial, si <math>\vec{n}</math> es el vector perpendicular a la superficie plana de la sección | ||
| + | |||
| + | <center><math>v_n = \vec{v}\cdot\vec{n}\qquad\Rightarrow\qquad \Phi = \vec{v}\cdot\vec{n}S = \vec{v}\cdot\vec{S}</math></center> | ||
| + | |||
| + | donde hemos definido el vector superficie como aquél que tiene por módulo el área de la superficie y como dirección y sentido los de un vector unitario normal a ésta. | ||
| + | |||
| + | <center><math>\vec{S}=S\vec{n}</math></center> | ||
| + | |||
| + | [[Archivo:flujo-general.png|right]] | ||
| + | |||
| + | La siguiente generalización consiste en suponer que la velocidad no tiene una distribución uniforme, sino que varía de un punto a otro y que la superficie sobre la que hallamos el flujo no es un plano sino que puede ser curvada. En ese caso, lo que se hace es descomponer la superficie en trocitos muy pequeños (elementos de superficie), para cada uno de los cuales se aplica la fórmula anterior | ||
| + | |||
| + | <center><math>\mathrm{d}\Phi = \vec{v}\cdot\mathrm{d}\vec{S}\qquad\qquad \mathrm{d}\vec{S}=\mathrm{d}S\,\vec{n}</math></center> | ||
| + | |||
| + | y el flujo total será la suma (integral) para toda la superficie. | ||
| + | |||
| + | <center><math>\Phi = \int_S \vec{v}\cdot\mathrm{d}\vec{S}</math></center> | ||
| + | |||
| + | Como caso particular importante tenemos el de una superficie cerrada | ||
| + | |||
| + | <center><math>\Phi=\oint \vec{v}\cdot\mathrm{d}\vec{S}</math></center> | ||
| + | |||
| + | donde el círculo en la integral representa que la superficie es cerrada. En el caso de una superficie cerrada, se considera siempre el sentido de la normal hacia el exterior de la superficie. | ||
| + | |||
| + | {| class="bordeado" | ||
| + | |- | ||
| + | | [[Archivo:Flujo-cuadrado-d.png]] | ||
| + | | [[Archivo:Flujo-cuadrado-c.png]] | ||
| + | | [[Archivo:Flujo-cuadrado-a.png]] | ||
| + | |- | ||
| + | | <math>\Phi>0\,</math> | ||
| + | | <math>\Phi<0\,</math> | ||
| + | | <math>\Phi=0\,</math> | ||
| + | |} | ||
| + | Para el caso de la superficie cerrada, si <math>\Phi > 0</math> quiere decir que el campo sale, en promedio hacia afuera de la superficie. Se dice entonces que el campo posee ''manantiales'' en el volumen encerrado por la superficie (de los cuales “brota” el campo). Si <math>\Phi < 0</math> quiere decir que el campo, en promedio, va hacia adentro. En ese caso se dice que el campo tiene ''sumideros'' (en los que se “destruye” el campo). Si el flujo es nulo quiere decir que en el interioo del volumen hay tantos manantiales como sumideros | ||
| + | |||
| + | Geométricamente, el flujo de un campo a través de una superficie cerrada se puede representar como el número de líneas de campo que atraviesan dicha superficie. | ||
==Ley de Gauss== | ==Ley de Gauss== | ||
| Línea 25: | Línea 88: | ||
; <math>\vec{E}</math>: El campo eléctrico en los puntos de la superficie. Este campo será en general función de la posición, por lo que no puede extraerse de la integral. | ; <math>\vec{E}</math>: El campo eléctrico en los puntos de la superficie. Este campo será en general función de la posición, por lo que no puede extraerse de la integral. | ||
; <math>\cdot</math>: El campo eléctrico es un vector y el diferencial de superficie también lo es. El flujo en cambio, es un número con signo. El producto escalar nos garantiza el carácter escalar del resultado. | ; <math>\cdot</math>: El campo eléctrico es un vector y el diferencial de superficie también lo es. El flujo en cambio, es un número con signo. El producto escalar nos garantiza el carácter escalar del resultado. | ||
| - | + | ; <math>\mathrm{d}\vec{S}</math>: Cuando se integra sobre una superficie, se divide ésta en elementos de área <math>\mathrm{d}S</math>. Se define el vector diferencial de superficie como uno que tiene por módulo el área del elemento, por dirección la perpendicular a la superficie y por sentido el que va hacia el exterior | |
<center><math>\mathrm{d}\vec{S}=\vec{n}\,\mathrm{d}S</math></center> | <center><math>\mathrm{d}\vec{S}=\vec{n}\,\mathrm{d}S</math></center> | ||
| Línea 36: | Línea 99: | ||
:* Si la carga neta encerrada es negativa: El flujo neto es hacia el interior y el campo es convergente (caso de <math>S_3</math>). | :* Si la carga neta encerrada es negativa: El flujo neto es hacia el interior y el campo es convergente (caso de <math>S_3</math>). | ||
| - | :* Si la carga neta encerrada es cero: El flujo es nulo y hay tanto campo | + | :* Si la carga neta encerrada es cero: El flujo es nulo y hay tanto campo que entra como que sale. Es importante recordar que un flujo nulo no implica un campo nulo |
<center><math>\oint_S \vec{E}\cdot\mathrm{d}\vec{S} = 0\qquad\not\Rightarrow\qquad\vec{E}=\vec{0}</math></center> | <center><math>\oint_S \vec{E}\cdot\mathrm{d}\vec{S} = 0\qquad\not\Rightarrow\qquad\vec{E}=\vec{0}</math></center> | ||
| Línea 48: | Línea 111: | ||
<center><math>\frac{1}{4\pi\varepsilon_0} = k_e\simeq 9\times 10^9\frac{\mathrm{N}\cdot\mathrm{m}^2}{\mathrm{C}^2}</math></center> | <center><math>\frac{1}{4\pi\varepsilon_0} = k_e\simeq 9\times 10^9\frac{\mathrm{N}\cdot\mathrm{m}^2}{\mathrm{C}^2}</math></center> | ||
| - | == | + | ===Prueba de la ley de Gauss=== |
| - | + | La ley de Gauss puede demostrarse para el caso electrostático a partir de la ley de Coulomb y el principio de superposición. No obstante, su demostración requiere técnicas algo más avanzadas que las que aquí se exponen, por lo que solo daremos las ideas principales. | |
| - | + | [[Archivo:flujo-carga-puntual-02.png|right]] | |
| - | + | Partimos del campo eléctrico de una carga puntual | |
| - | + | <center><math>\vec{E}=\frac{1}{4\pi\varepsilon_0}\,\frac{q\vec{u}_r}{r^2}</math></center> | |
| - | + | Si consideramos el flujo de este campo eléctrico a través de una superficie esférica concéntrica con la carga tenemos | |
| - | <center> | + | <center><math>\Phi = \frac{q}{4\pi\varepsilon_0}\oint_{r=\mathrm{cte}} \frac{\vec{u}_r\cdot\mathrm{d}\vec{S}}{r^2}</math></center> |
| - | + | Ahora bien, para una superficie esférica, el diferencial de superficie es un vector radial y hacia afuera | |
| - | <center><math>\mathrm{d}\vec{S}=\ | + | <center><math>\mathrm{d}\vec{S}=\mathrm{d}S\,\vec{u}_r\qquad\Rightarrow\qquad \mathrm{d}\vec{S}\cdot\vec{u}_r=\mathrm{d}S</math></center> |
| - | + | por lo que la integral se reduce a una escalar | |
| - | <center><math>\ | + | <center><math>\Phi = \frac{q}{4\pi\varepsilon_0}\oint_{r=\mathrm{cte}} \frac{\mathrm{d}S}{r^2}</math></center> |
| - | + | Por otra parte, al tratarse de una superficie esférica, r es el mismo para todos los puntos de la esfera, por lo que puede salir de esta integral y quedar | |
| - | <center><math>\ | + | <center><math>\Phi = \frac{q}{4\pi\varepsilon_0r^2}\oint_{r=\mathrm{cte}} \mathrm{d}S=\frac{qS}{4\pi\varepsilon_0r^2}</math></center> |
| - | + | Si sustituimos el área de la esfera | |
| - | <center><math> | + | <center><math>S=4\pi r^2\qquad\Rightarrow\qquad\Phi =\frac{q}{\varepsilon_0}</math></center> |
| - | + | Es decir, resulta que para una superficie esférica concéntrica con la carga el flujo es el mismo ''independientemente del radio de la esfera''. A medida que nos alejamos de la carga, el campo decrece como la inversa del cuadrado de la distancia, pero el área de la esfera crece como el cuadrado de la misma distancia, por lo que los dos factores se cancelan. | |
| - | + | Podemos preguntarnos qué propiedades del campo eléctrico son las mismas independientemente de la distancia a la carga. Una es la magnitud de la carga que lo crea. Otra es el número de líneas de campo que atraviesan la superficie, que es lo que mide el flujo. Hemos obtenido que ambas cantidades son proporcionales. | |
| - | + | ||
| - | + | El resultado se extiende ahora a otras superficies que no son esferas concéntricas. Puede demostrarse que el resultado es el mismo: para toda superficie cerrada S que envuelva a la carga | |
| - | + | <center><math>\Phi = \frac{q}{\varepsilon_0}\qquad\qquad (q\in S)</math></center> | |
| - | + | <center> | |
| + | [[Archivo:flujo-esfera.png|400px]][[Archivo:flujo-octaedro.gif|400px]]</center> | ||
| - | + | Este resultado también vale si la carga es negativa. En ese caso, las líneas van hacia adentro y el flujo es negativo. | |
| - | + | {| class="bordeado" | |
| + | |- | ||
| + | | [[Archivo:flujo-interior.png|400px]] | ||
| + | | [[Archivo:flujo-exterior.png|400px]] | ||
| + | |- | ||
| + | | <math>\Phi>0\,</math> | ||
| + | | <math>\Phi=0\,</math> | ||
| + | |} | ||
| - | + | Por otro lado, si tomamos una superficie que no envuelva a la carga, el número de líneas de campo que atraviesan la superficie hacia adentro iguala al de las que lo hacen hacia afuera, por lo que | |
| - | <center> | + | <center><math>\Phi = 0\qquad\qquad (q\not\in S)</math></center> |
| - | + | Esto para una carga individual. Si consideramos una distribución de cargas, aplicamos el principio de superposición | |
| - | <center><math>\vec{ | + | <center><math>\vec{E}=\vec{E}_1+\vec{E}_2+\cdots = \sum_i\vec{E}_i</math></center> |
| - | + | Este principio también se aplica al flujo del campo eléctrico | |
| - | + | <center><math>\Phi = \oint \vec{E}\cdot\mathrm{d}\vec{S}=\sum_i \oint \vec{E}_i\cdot\mathrm{d}\vec{S}</math></center> | |
| - | + | ||
| - | + | Para los flujos de las cargas individuales habrá cargas que están contenidas dentro de la superficie y cargas que estarán. | |
| - | <center> | + | <center>[[Archivo:cargas-interiores.png|400px]]</center> |
| + | Las que están dentro dan una contribución al flujo mientras que las exteriores añaden una cantidad nula | ||
| + | Por ello | ||
| - | |||
| - | <center><math> | + | <center><math>\Phi = \sum_{q_i\in S}\frac{q_i}{\varepsilon_0}+\sum_{q_i\not\in S}0=\frac{Q_\mathrm{int}}{\varepsilon_0}</math></center> |
| - | + | siendo | |
| - | <center><math>\ | + | <center><math>Q_\mathrm{int}=\sum_{q_i\in S}q_i</math></center> |
| - | + | la carga neta encerrada dentro de la superficie. | |
| - | + | ==Campo de cargas puntuales== | |
| + | La ley de Gauss tiene validez universal y por tanto puede tomarse como punto de partida, junto con el resto de las ecuaciones de Maxwell, para deducir el resto de ecuaciones del electromagnetismo. | ||
| - | + | Una de las primeras aplicaciones de la ley de Gauss es la obtención del campo eléctrico creado por una carga puntual. Es decir, suponiendo que no la conociéramos de antes, podemos deducirla | |
| - | + | Por la simetría del sistema, el campo creado por una carga va a ser central | |
| - | + | <center><math>\vec{E}(\vec{r})=E(r)\vec{u}_r</math></center> | |
| - | + | siendo <math>r</math> la distancia a la carga, <math>\vec{r}</math> el vector de posición respecto a la carga y <math>\vec{u}_r</math> el unitario en la dirección radial. | |
| - | + | ||
| - | + | De acuerdo con la ley de Gauss, el flujo a través de cualquier superficie cerrada que envuelva a esta carga será el mismo. Si consideramos superficies esféricas concéntricas de radio cada vez más grande, el área de cada una crece como el cuadrado del radio, pero el flujo no cambia. Por tanto, el campo eléctrico de una carga puntual debe decaer como el cuadrado de la distancia a la carga. | |
| - | : | + | <center>[[Archivo:flujo-carga-puntual-02.png]]</center> |
| - | + | Matemáticamente | |
| - | + | <center><math>\mathrm{d}\vec{S}=\vec{u}_r\,\mathrm{d}S\qquad\qquad \frac{q}{\varepsilon_0}=\oint_S\vec{E}\cdot\mathrm{d}\vec{S}=\oint_S E(r)\,\mathrm{d}S</math></center> | |
| - | < | + | y puesto que <math>E(r)</math> tiene el mismo valor para todos los puntos de la superficie esférica puede salir de la integral y queda |
| - | + | <center><math>\oint_S E(r)\,\mathrm{d}S = E(r) S = 4\pi r^2 E = \frac{q}{\varepsilon_0}\qquad\Rightarrow\qquad \vec{E}=\frac{q}{4\pi r^2}\vec{u}_r=\frac{1}{4\pi\varepsilon_0}\,\frac{q\vec{r}}{|\vec{r}|^3}</math></center> | |
| - | + | Una vez que tenemos el campo de una carga puntual situada en el origen de coordenadas podemos obtener el campo para cualquier otro punto sin más que trasladar los vectores | |
| - | <center><math>\vec{E} | + | <center><math>\vec{r}\to \vec{r}-\vec{r}_1\qquad\Rightarrow\qquad \vec{E}(\vec{r})=\frac{1}{4\pi\varepsilon_0}\,\frac{q(\vec{r}-\vec{r}_1)}{|\vec{r}-\vec{r}_1|^3}</math></center> |
| - | + | ==Aplicaciones de la ley de Gauss== | |
| + | La ley de Guauss es siempre cierta, pero no siempre es útil. Nos proporciona el valor de la integral de un campo, pero no el valor del propio campo. Existen muchas funciones diferentes que tienen la misma integral definida. Por ello, en principio, no podemos extraer el campo de la integral y “despejarlo”. | ||
| - | + | La excepción la dan las situaciones con simetrías. Se dice que una distribución es simétrica cuando efectuando un cambio en la posición no se percibe ningún cambio en la distribución. Así tenemos: | |
| - | + | ;Simetría traslacional: es aquella en que el sistema es invariante ante un desplazamiento rectilíneo. Por ejemplo, imaginemos una línea cargada rectilínea y de longitud infinita (que modelaría un cable, por ejemplo). Si nos movemos paralelamente al cable no vemos ningún cambio. Se dice entonces que hay simetría traslacional. Si en vez de un cable infinito tenemos un segmento de longitud finita ya no es cierto, pues no es lo mismo estar junto a la mitad del cable que junto a un extremo o más allá. | |
| - | + | ;Simetría rotacional: es aquella en que el sistema es invariante ante una rotación. Siguiendo con el ejemplo del cable, no apreciamos ningún cambio si rotamos en torno a él, manteniéndonos a la misma distancia. | |
| - | + | ||
| - | + | ||
| - | <center><math>\vec{E} | + | ;Simetría esférica: corresponde a que haya simetría rotacional respecto a cualquier dirección. Una esfera cargada uniformemente se ve igual se mire desde donde se mire. |
| + | |||
| + | ===Simetría esférica=== | ||
| + | En los casos de simetría esférica, el procedimiento de cálculo del campo eléctrico es el siguiente, desarrollado en [[Campo_de_distribuciones_con_simetría_esférica|un problema]] | ||
| + | |||
| + | [[Archivo:esfera-densidad-radial-01.png|right]] | ||
| + | |||
| + | Si la distribución de carga posee simetría esférica o de revolución, de manera que se ve igual desde todas las direcciones, el campo eléctrico que produce va en la dirección radial y depende solo de la distancia al centro de la distribución | ||
| + | |||
| + | <center><math>\vec{E}(\vec{r})=E(r)\vec{u}_r</math></center> | ||
| - | + | Este es el caso, por ejemplo, de una carga puntual. La cantidad <math>E(r)</math> no es el módulo del campo, sino su componente radial, ya que tiene un signo que nos dice si va hacia afuera (caso de una carga positiva) o hacia adentro (caso de una carga negativa). | |
| - | + | Hay que remarcar que no todas las distribuciones de carga en una esfera poseen simetría esférica. Por ejemplo, una esfera cargada positivamente en su hemisferio “norte” y negativamente en el “sur” no posee simetría esférica, ya que no todas las direcciones son equivalentes. No se ve lo mismo desde el norte que desde el sur o desde el ecuador. | |
| - | + | Suponiendo que sí existe simetría esférica, el flujo del campo eléctrico a través de una superficie esférica puede hallarse explícitamente. Si tomamos una superficie esférica de radio <math>r</math> concéntrica con la distribución, el diferencial de superficie, ortogonal a ésta, va en la dirección radial | |
| - | + | ||
| - | + | <center><math>\mathrm{d}\vec{S}=\mathrm{d}S\,\vec{u}_r</math></center> | |
| - | + | Por ello, el flujo se reduce a una integral de un escalar | |
| - | + | <center><math>\oint \vec{E}\cdot\mathrm{d}\vec{S}=\oint (E(r)\vec{u}_r)\cdot(\mathrm{d}S\,\vec{u}_r)=\oint E(r)\mathrm{d}S</math></center> | |
| - | + | Ahora bien, dado que la superficie de integración es una esfera, todos sus puntos se encuentran a la misma distancia del centro y por tanto, el valor de la componente radial del campo, <math>E(r)</math>, tiene el mismo valor para todos ellos y puede extraerse de la integral | |
| - | + | <center><math>\oint E(r)\mathrm{d}S = E(r)\oint \mathrm{d}S= 4\pi r^2 E(r)</math></center> | |
| - | + | Hay que recordar que el campo no es el mismo para todos los puntos de la superficie esférica, ya que su dirección y sentido cambian de un punto a otro. Lo que es constante es el valor de su módulo. | |
| - | + | Llevando esto a la ley de Gauss nos queda | |
| - | + | <center><math>4\pi r^2 E = \frac{Q_\mathrm{int}(r)}{\varepsilon_0} \qquad\Rightarrow\qquad \vec{E}=\frac{1}{4\pi\varepsilon_0}\,\frac{Q_\mathrm{int}(r)}{r^2}\vec{u}_r</math></center> | |
| - | + | Por tanto, para los sistemas con simetría esférica (y solo para ellos) el campo para cada distancia del centro equivale al de una carga puntual cuyo valor es igual al de toda la carga contenida en el volumen <math>r'< r</math>. | |
| - | + | Como ejemplos de sistemas con simetría esférica tenemos: | |
| + | * Una [[Campo_de_distribuciones_con_simetría_esférica#Una_carga_puntual|carga puntual]] | ||
| + | * Una [[Campo_de_distribuciones_con_simetría_esférica#Una_superficie_esf.C3.A9rica|superficie esférica cargada uniformemente]] | ||
| + | * Dos [[Campo_de_distribuciones_con_simetría_esférica#Dos_superficies_conc.C3.A9ntricas_con_cargas_opuestas|superficies esféricas concéntricas]] | ||
| + | * Una [[Campo_de_distribuciones_con_simetría_esférica#Una_esfera_maciza_cargada_uniformemente|esfera maciza cargada uniformemente]] | ||
| - | + | Cuando tenemos un sistema que es una combinación de [[Dos_esferas_huecas|esferas descentradas]], no podemos hacer uso de la ley de Gauss para hallar el campo de la distribución completa de una vez, ya que no hay simetría. Lo que sí se puede hacer es descomponer el sistema en partes, hallar el campo para cada esfera por separado por ley de Gauss y posteriormente aplicar el principio de superposición. | |
| - | + | ===Simetría traslacional=== | |
| + | La simetría traslacional es la que se tiene cuando el sistema no cambia al realizar un desplazamiento cualquiera en una cierta dirección (típicamente de forma paralela al eje Z, que suele tomarse como eje de simetría). | ||
| - | + | El ejemplo más simple es el de un hilo rectilíneo infinitamente largo, dotado de una densidad lineal uniforme de carga, <math>\lambda_0</math>. Este modelo sirve para aproximar el campo eléctrico debido a un cable como los de los tendidos de alta tensión. | |
| - | + | Si situamos el eje OZ sobre el hilo, la simetría implica que el campo no depende de la coordenada z. | |
| - | + | Por otro lado, para cualquier punto P del espacio, el campo debido a un elemento del hilo se suma con el de otro elemento situado simétricamente, resultando un campo perpendicular al segmento. Como además hay simetría de revolución, este campo solo puede ser radial. | |
| - | + | <center>[[Archivo:campoE-hilo-recto.png]]</center> | |
| - | + | ||
| - | + | Empleando coordenadas cilíndricas | |
| - | <center><math> | + | <center><math>\vec{E}=E(\rho)\vec{u}_\rho</math></center> |
| - | + | [[Archivo:flujoE-hilo-recto.png|right]] | |
| - | + | Si ahora aplicamos la ley de Gauss a una superficie cilíndrica de radio <math>\rho</math> y altura <math>h</math> concéntrica con el hilo solo hay flujo de campo a través de la cara lateral, siendo su valor | |
| - | + | <center><math>\oint \vec{E}\cdot\mathrm{d}\vec{S}=\int E(\rho)\,\mathrm{d}S=2\pi\rho h E(\rho)</math></center> | |
| - | + | Este flujo es igual a la carga encerrada por el cilindro, dividida por la permitividad del vacío | |
| - | + | <center><math>\frac{Q_\mathrm{int}}{\varepsilon_0}=\frac{\lambda_0h}{\varepsilon_0}</math></center> | |
| - | + | Igualamos y despejamos y queda el campo | |
| - | + | <center><math>\vec{E}=\frac{\lambda_0}{2\pi\varepsilon_0\rho}\vec{u}_\rho</math></center> | |
| - | + | Este campo es radial y hacia afuera (si la densidad de carga es positiva) y decae con la distancia al hilo como la inversa de ésta (no como la inversa del cuadrado). | |
| - | + | Podemos escribirlo en cartesianas observando que | |
| - | <center><math>\rho = \frac{ | + | <center><math>\vec{E}=\frac{\lambda_0}{2\pi\varepsilon_0}\frac{\vec{u}_\rho}{\rho}=\frac{\lambda_0}{2\pi\varepsilon_0}\,\frac{\rho\vec{u}_\rho}{\rho^2} = \frac{\lambda_0}{2\pi\varepsilon_0}\left(\frac{x\vec{\imath}+y\vec{\jmath}}{x^2+y^2}\right)</math></center> |
| + | Si tenemos más de un hilo, el campo total puede hallarse aplicando el principio de superposición. | ||
[[Categoría:Electrostática en el vacío (GIE)]] | [[Categoría:Electrostática en el vacío (GIE)]] | ||
última version al 12:26 13 abr 2018
Contenido |
1 Flujo de un campo vectorial
Un concepto básico en electromagnetismo y en mecánica de fluidos es el de flujo. La idea es sencilla: el flujo de un campo vectorial es una medida de “cuánto campo” atraviesa una superficie cerrada.
Para definir con precisión lo que se entiende por “cuánto campo”, consideremos en primer lugar el ejemplo sencillo de una tubería por la que fluye agua de manera constante. Queremos saber cuánta agua sale por una boca que es un corte transversal de la tubería. En este caso el caudal, el volumen de agua que pasa en un intervalo dt es la contenida en una porción de tubería adyacente al orificio de salida
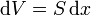
la longitud de la porción corresponde a la que le da tiempo a llegar a la salida en dt
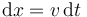
de forma que el caudal es igual a
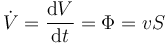
La cantidad de agua es mayor cuanto más rápido se mueva el agua y cuando mayor sea la sección de la tubería.
Supongamos ahora que la boca de la tubería no es transversal sino oblicua. No podemos seguir usando la expresión anterior, ya que ahora la sección tiene mayor área, pero la cantidad de agua que sale por la boca del tubo debería ser la misma que antes. La corrección que hay que hacer viene de que el vector velocidad puede descomponerse en dos partes, una perpendicular a la superficie y una tangencial a ella. Sólo la componente normal atraviesa la superficie. La tangencial “resbala” sobre ella. Por tanto, debemos escribir el flujo como
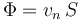
En forma vectorial, si 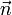 es el vector perpendicular a la superficie plana de la sección
es el vector perpendicular a la superficie plana de la sección

donde hemos definido el vector superficie como aquél que tiene por módulo el área de la superficie y como dirección y sentido los de un vector unitario normal a ésta.
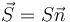
La siguiente generalización consiste en suponer que la velocidad no tiene una distribución uniforme, sino que varía de un punto a otro y que la superficie sobre la que hallamos el flujo no es un plano sino que puede ser curvada. En ese caso, lo que se hace es descomponer la superficie en trocitos muy pequeños (elementos de superficie), para cada uno de los cuales se aplica la fórmula anterior

y el flujo total será la suma (integral) para toda la superficie.
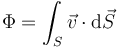
Como caso particular importante tenemos el de una superficie cerrada
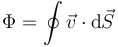
donde el círculo en la integral representa que la superficie es cerrada. En el caso de una superficie cerrada, se considera siempre el sentido de la normal hacia el exterior de la superficie.
| 
| 
|
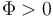
| 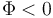
| 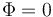
|
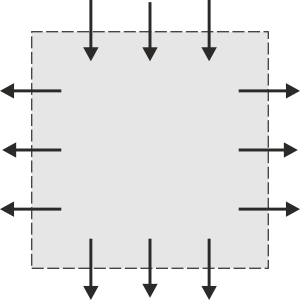
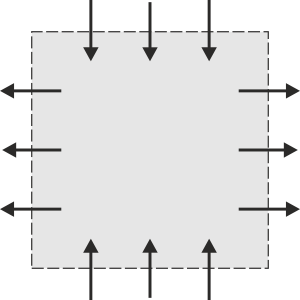
Para el caso de la superficie cerrada, si Φ > 0 quiere decir que el campo sale, en promedio hacia afuera de la superficie. Se dice entonces que el campo posee manantiales en el volumen encerrado por la superficie (de los cuales “brota” el campo). Si Φ < 0 quiere decir que el campo, en promedio, va hacia adentro. En ese caso se dice que el campo tiene sumideros (en los que se “destruye” el campo). Si el flujo es nulo quiere decir que en el interioo del volumen hay tantos manantiales como sumideros
Geométricamente, el flujo de un campo a través de una superficie cerrada se puede representar como el número de líneas de campo que atraviesan dicha superficie.
2 Ley de Gauss
Una propiedad del campo eléctrico que se desprende del trazado de sus líneas de campo es la siguiente.
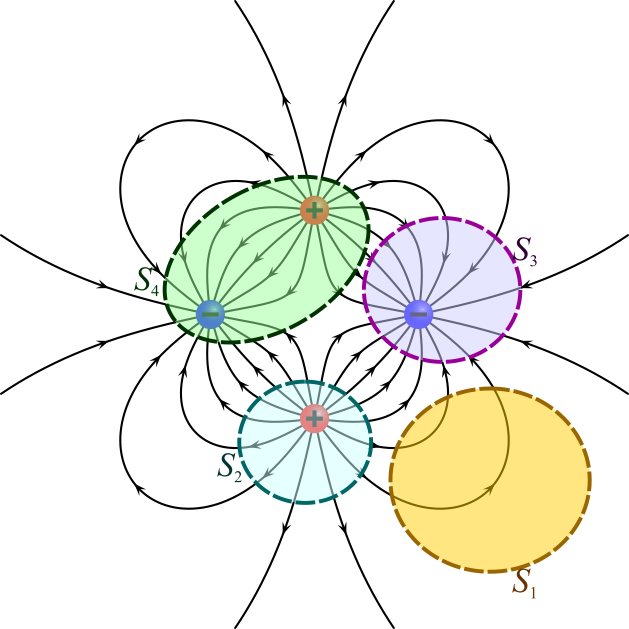
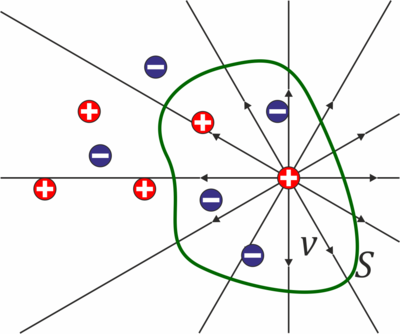
Consideremos, por ejemplo, el caso de cuatro cargas ilustrado anteriormente
- Si tomamos la superficie cerrada S1, vemos que no encierra carga alguna, y que en ella hay tantas líneas de campo que entran como las que salen.
- En la superficie S2, que envuelve a la carga positiva, las líneas de campo atraviesan la superficie hacia el exterior. Se dice que en esta región el campo es divergente.
- En S3, en cambio, se envuelve una carga negativa y en ella el campo es convergente, atravesando las líneas de campo la superficie hacia adentro.
- En S4 se envuelve una carga neta 0, y vemos que en ella también hay tantas líneas que entran como que salen.
Vemos que el hecho de que las líneas atraviesen la superficie hacia afuera o hacia adentro depende de las cargas que haya en el interior, y que si es nula (bien porque no hay nada, bien porque hay tantas positivas como negativas) hay tantas que entran como que salen.
Este es un resultado general. Matemáticamente se expresa con el concepto de flujo que es una medida de cuánto campo atraviesa una superficie. La ley física que describe este fenómeno es la ley de Gauss
- Ley de Gauss: El flujo del campo eléctrico a través de una superficie cerrada es proporcional a la cantidad de carga encerrada por la superficie.
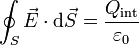
Analizando cada uno de los términos de esta ecuación tenemos:
-
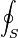
- El símbolo de integral con un círculo representa la integración sobre una superficie cerrada.
-
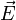
- El campo eléctrico en los puntos de la superficie. Este campo será en general función de la posición, por lo que no puede extraerse de la integral.
-

- El campo eléctrico es un vector y el diferencial de superficie también lo es. El flujo en cambio, es un número con signo. El producto escalar nos garantiza el carácter escalar del resultado.
-
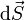
- Cuando se integra sobre una superficie, se divide ésta en elementos de área dS. Se define el vector diferencial de superficie como uno que tiene por módulo el área del elemento, por dirección la perpendicular a la superficie y por sentido el que va hacia el exterior
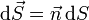
- (¡ojo a la diferencia entre
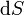 y
y 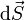 !).
!).
- Qint
- es la carga encerrada por la superficie. Ojo que no es toda la carga del sistema. Puede haber cargas en el exterior, que producen campo en la superficie (por ejemplo, las cuatro cargas respecto de la S1 anterior), pero que no están encerradas por ella. Aquí:
- Si la carga neta encerrada es positiva: El flujo neto es hacia el exterior y el campo es divergente (caso de la superficie S2). Esto no excluye que pueda contener cargas negativas y que haya algunas líneas de campo hacia adentro, como en la superficie S5.
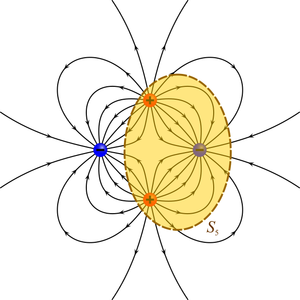
- Si la carga neta encerrada es negativa: El flujo neto es hacia el interior y el campo es convergente (caso de S3).
- Si la carga neta encerrada es cero: El flujo es nulo y hay tanto campo que entra como que sale. Es importante recordar que un flujo nulo no implica un campo nulo
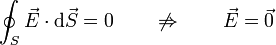

- La constante de proporcionalidad es una constante universal denominada permitividad del vacío, que tiene un valor exacto
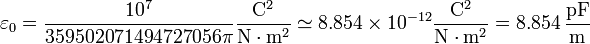
- Aunque se suele aproximar en la forma más sencilla
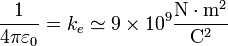
2.1 Prueba de la ley de Gauss
La ley de Gauss puede demostrarse para el caso electrostático a partir de la ley de Coulomb y el principio de superposición. No obstante, su demostración requiere técnicas algo más avanzadas que las que aquí se exponen, por lo que solo daremos las ideas principales.
Partimos del campo eléctrico de una carga puntual
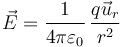
Si consideramos el flujo de este campo eléctrico a través de una superficie esférica concéntrica con la carga tenemos
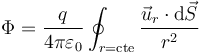
Ahora bien, para una superficie esférica, el diferencial de superficie es un vector radial y hacia afuera
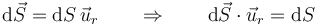
por lo que la integral se reduce a una escalar
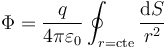
Por otra parte, al tratarse de una superficie esférica, r es el mismo para todos los puntos de la esfera, por lo que puede salir de esta integral y quedar
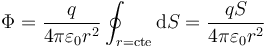
Si sustituimos el área de la esfera
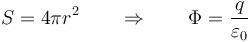
Es decir, resulta que para una superficie esférica concéntrica con la carga el flujo es el mismo independientemente del radio de la esfera. A medida que nos alejamos de la carga, el campo decrece como la inversa del cuadrado de la distancia, pero el área de la esfera crece como el cuadrado de la misma distancia, por lo que los dos factores se cancelan.
Podemos preguntarnos qué propiedades del campo eléctrico son las mismas independientemente de la distancia a la carga. Una es la magnitud de la carga que lo crea. Otra es el número de líneas de campo que atraviesan la superficie, que es lo que mide el flujo. Hemos obtenido que ambas cantidades son proporcionales.
El resultado se extiende ahora a otras superficies que no son esferas concéntricas. Puede demostrarse que el resultado es el mismo: para toda superficie cerrada S que envuelva a la carga



Este resultado también vale si la carga es negativa. En ese caso, las líneas van hacia adentro y el flujo es negativo.
| 
|
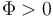
| 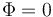
|
Por otro lado, si tomamos una superficie que no envuelva a la carga, el número de líneas de campo que atraviesan la superficie hacia adentro iguala al de las que lo hacen hacia afuera, por lo que

Esto para una carga individual. Si consideramos una distribución de cargas, aplicamos el principio de superposición
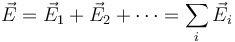
Este principio también se aplica al flujo del campo eléctrico
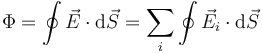
Para los flujos de las cargas individuales habrá cargas que están contenidas dentro de la superficie y cargas que estarán.
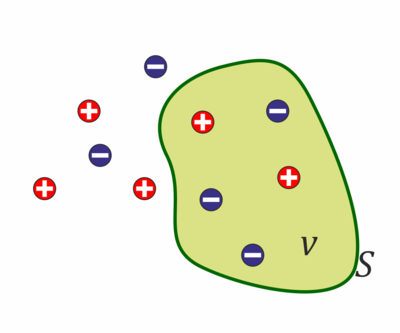
Las que están dentro dan una contribución al flujo mientras que las exteriores añaden una cantidad nula Por ello
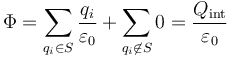
siendo

la carga neta encerrada dentro de la superficie.
3 Campo de cargas puntuales
La ley de Gauss tiene validez universal y por tanto puede tomarse como punto de partida, junto con el resto de las ecuaciones de Maxwell, para deducir el resto de ecuaciones del electromagnetismo.
Una de las primeras aplicaciones de la ley de Gauss es la obtención del campo eléctrico creado por una carga puntual. Es decir, suponiendo que no la conociéramos de antes, podemos deducirla
Por la simetría del sistema, el campo creado por una carga va a ser central
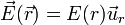
siendo r la distancia a la carga,  el vector de posición respecto a la carga y
el vector de posición respecto a la carga y 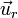 el unitario en la dirección radial.
el unitario en la dirección radial.
De acuerdo con la ley de Gauss, el flujo a través de cualquier superficie cerrada que envuelva a esta carga será el mismo. Si consideramos superficies esféricas concéntricas de radio cada vez más grande, el área de cada una crece como el cuadrado del radio, pero el flujo no cambia. Por tanto, el campo eléctrico de una carga puntual debe decaer como el cuadrado de la distancia a la carga.
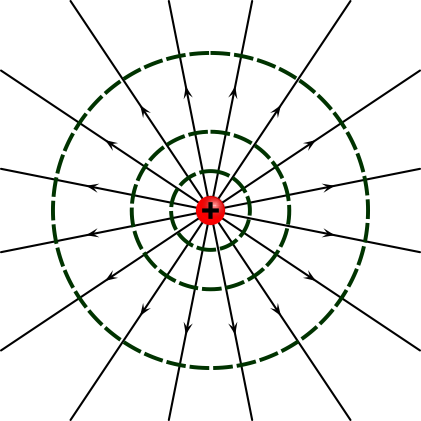
Matemáticamente
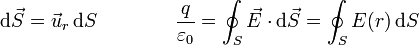
y puesto que E(r) tiene el mismo valor para todos los puntos de la superficie esférica puede salir de la integral y queda
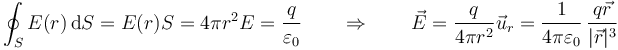
Una vez que tenemos el campo de una carga puntual situada en el origen de coordenadas podemos obtener el campo para cualquier otro punto sin más que trasladar los vectores
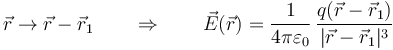
4 Aplicaciones de la ley de Gauss
La ley de Guauss es siempre cierta, pero no siempre es útil. Nos proporciona el valor de la integral de un campo, pero no el valor del propio campo. Existen muchas funciones diferentes que tienen la misma integral definida. Por ello, en principio, no podemos extraer el campo de la integral y “despejarlo”.
La excepción la dan las situaciones con simetrías. Se dice que una distribución es simétrica cuando efectuando un cambio en la posición no se percibe ningún cambio en la distribución. Así tenemos:
- Simetría traslacional
- es aquella en que el sistema es invariante ante un desplazamiento rectilíneo. Por ejemplo, imaginemos una línea cargada rectilínea y de longitud infinita (que modelaría un cable, por ejemplo). Si nos movemos paralelamente al cable no vemos ningún cambio. Se dice entonces que hay simetría traslacional. Si en vez de un cable infinito tenemos un segmento de longitud finita ya no es cierto, pues no es lo mismo estar junto a la mitad del cable que junto a un extremo o más allá.
- Simetría rotacional
- es aquella en que el sistema es invariante ante una rotación. Siguiendo con el ejemplo del cable, no apreciamos ningún cambio si rotamos en torno a él, manteniéndonos a la misma distancia.
- Simetría esférica
- corresponde a que haya simetría rotacional respecto a cualquier dirección. Una esfera cargada uniformemente se ve igual se mire desde donde se mire.
4.1 Simetría esférica
En los casos de simetría esférica, el procedimiento de cálculo del campo eléctrico es el siguiente, desarrollado en un problema
Si la distribución de carga posee simetría esférica o de revolución, de manera que se ve igual desde todas las direcciones, el campo eléctrico que produce va en la dirección radial y depende solo de la distancia al centro de la distribución
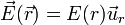
Este es el caso, por ejemplo, de una carga puntual. La cantidad E(r) no es el módulo del campo, sino su componente radial, ya que tiene un signo que nos dice si va hacia afuera (caso de una carga positiva) o hacia adentro (caso de una carga negativa).
Hay que remarcar que no todas las distribuciones de carga en una esfera poseen simetría esférica. Por ejemplo, una esfera cargada positivamente en su hemisferio “norte” y negativamente en el “sur” no posee simetría esférica, ya que no todas las direcciones son equivalentes. No se ve lo mismo desde el norte que desde el sur o desde el ecuador.
Suponiendo que sí existe simetría esférica, el flujo del campo eléctrico a través de una superficie esférica puede hallarse explícitamente. Si tomamos una superficie esférica de radio r concéntrica con la distribución, el diferencial de superficie, ortogonal a ésta, va en la dirección radial
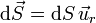
Por ello, el flujo se reduce a una integral de un escalar
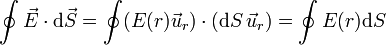
Ahora bien, dado que la superficie de integración es una esfera, todos sus puntos se encuentran a la misma distancia del centro y por tanto, el valor de la componente radial del campo, E(r), tiene el mismo valor para todos ellos y puede extraerse de la integral
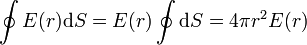
Hay que recordar que el campo no es el mismo para todos los puntos de la superficie esférica, ya que su dirección y sentido cambian de un punto a otro. Lo que es constante es el valor de su módulo.
Llevando esto a la ley de Gauss nos queda
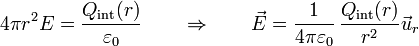
Por tanto, para los sistemas con simetría esférica (y solo para ellos) el campo para cada distancia del centro equivale al de una carga puntual cuyo valor es igual al de toda la carga contenida en el volumen r' < r.
Como ejemplos de sistemas con simetría esférica tenemos:
- Una carga puntual
- Una superficie esférica cargada uniformemente
- Dos superficies esféricas concéntricas
- Una esfera maciza cargada uniformemente
Cuando tenemos un sistema que es una combinación de esferas descentradas, no podemos hacer uso de la ley de Gauss para hallar el campo de la distribución completa de una vez, ya que no hay simetría. Lo que sí se puede hacer es descomponer el sistema en partes, hallar el campo para cada esfera por separado por ley de Gauss y posteriormente aplicar el principio de superposición.
4.2 Simetría traslacional
La simetría traslacional es la que se tiene cuando el sistema no cambia al realizar un desplazamiento cualquiera en una cierta dirección (típicamente de forma paralela al eje Z, que suele tomarse como eje de simetría).
El ejemplo más simple es el de un hilo rectilíneo infinitamente largo, dotado de una densidad lineal uniforme de carga, λ0. Este modelo sirve para aproximar el campo eléctrico debido a un cable como los de los tendidos de alta tensión.
Si situamos el eje OZ sobre el hilo, la simetría implica que el campo no depende de la coordenada z.
Por otro lado, para cualquier punto P del espacio, el campo debido a un elemento del hilo se suma con el de otro elemento situado simétricamente, resultando un campo perpendicular al segmento. Como además hay simetría de revolución, este campo solo puede ser radial.
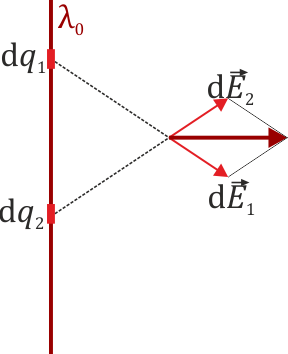
Empleando coordenadas cilíndricas
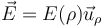
Si ahora aplicamos la ley de Gauss a una superficie cilíndrica de radio ρ y altura h concéntrica con el hilo solo hay flujo de campo a través de la cara lateral, siendo su valor
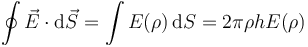
Este flujo es igual a la carga encerrada por el cilindro, dividida por la permitividad del vacío
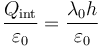
Igualamos y despejamos y queda el campo
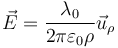
Este campo es radial y hacia afuera (si la densidad de carga es positiva) y decae con la distancia al hilo como la inversa de ésta (no como la inversa del cuadrado).
Podemos escribirlo en cartesianas observando que

Si tenemos más de un hilo, el campo total puede hallarse aplicando el principio de superposición.