Primera Convocatoria Ordinaria 2017/18 (G.I.C.)
De Laplace
(→Armónicos en una cuerda tensa) |
(→Armónicos en una cuerda tensa) |
||
| Línea 24: | Línea 24: | ||
#los dos extremos están fijos. | #los dos extremos están fijos. | ||
#un extremo está fijo y el otro está libre. | #un extremo está fijo y el otro está libre. | ||
| + | |||
| + | ==[[ Granada en movimiento vertical (Ene. 2018 G.I.C.)| Granada en movimiento vertical ]]== | ||
| + | Una granada de masa <math>M</math> se lanza verticalmente desde el suelo con una velocidad de módulo | ||
| + | <math>v_0</math>. Se mueve sometida únicamente a la acción de la | ||
| + | gravedad. En el punto más alto de la trayectoria la granada explota en dos trozos con la | ||
| + | misma masa. Justo después de la explosión uno de los trozos se mueve verticalmente hacia arriba con una velocidad | ||
| + | de módulo <math>v_1</math>. Determina la velocidad en ese instante del otro trozo. | ||
última version al 16:20 3 abr 2018
1 Vuelco en plano inclinado
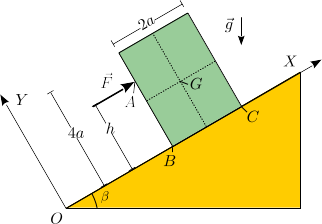
Un bloque rectangular, de masa m y lados 2a y 4a, descansa sobre
un plano inclinado un ángulo β respecto de la horizontal. Se aplica
sobre el punto A del bloque una fuerza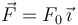 
, con F0 > 0. La fuerza es horizontal al plano inclinado y el punto A está a una
distancia h del plano. Consideramos en primera instancia que el contacto
entre el bloque y el plano es liso. El ángulo β cumple
- Dibuja el diagrama de cuerpo libre del bloque.
- Encuentra el valor de F0 para que haya equilibrio. Encuentra las expresiones de las fuerzas en esta situación.
- Con las fuerzas obtenidas en el apartado anterior, encuentra las condiciones que debe cumplir h para que el bloque no vuelque hacia la izquierda ni la derecha.
- Considera ahora que hay rozamiento entre el bloque y el plano inclinado, con coeficiente de rozamiento estático μ. Supongamos que F0 = mg. Determina las condiciones que deben cumplir μ y h para que haya equilibrio frente a deslizamiento y vuelco.
2 Armónicos en una cuerda tensa
Una cuerda de longitud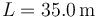 
tiene una densidad de masa lineal
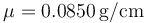y soporta una tensión 
.
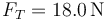Se excita un onda estacionaria en la cuerda.
Calcula las frecuencias de los dos primeros armónicos cuando
- los dos extremos están fijos.
- un extremo está fijo y el otro está libre.
3 Granada en movimiento vertical
Una granada de masa M se lanza verticalmente desde el suelo con una velocidad de módulo v0. Se mueve sometida únicamente a la acción de la gravedad. En el punto más alto de la trayectoria la granada explota en dos trozos con la misma masa. Justo después de la explosión uno de los trozos se mueve verticalmente hacia arriba con una velocidad de módulo v1. Determina la velocidad en ese instante del otro trozo.
