No Boletín - Péndulo simple (Ex.Ene/18)

De Laplace

(Diferencias entre revisiones)

última version al 16:49 22 feb 2018

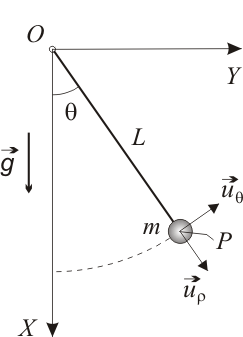
1 Enunciado

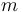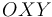Considérese un péndulo simple, constituido por una partícula $P\,$ (de masa $m\,$ ) que se halla suspendida de un punto fijo $O\,$ mediante un hilo inextensible (de longitud $L\,$ y masa despreciable). Bajo la acción de su propio peso, la partícula $P\,$ oscila en el plano vertical fijo $OXY\,$ (aceleración gravitatoria: 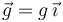$\vec{g}=g\,\vec{\imath}\,$ ). 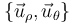Se propone la coordenada acimutal $\theta\,$ (definida en la figura) para describir la posición de la partícula $P\,$ , así como la base polar $\{\vec{u}_{\rho},\vec{u}_{\theta}\}\,$ para expresar las magnitudes vectoriales.

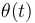De la segunda ley de Newton aplicada a la partícula $P\,$ y proyectada sobre la dirección acimutal, deduzca la ecuación diferencial de segundo orden que debe satisfacer la función $\theta(t)\,$ .
Y de la misma ley, pero proyectada sobre la dirección radial, deduzca el módulo de la tensión del hilo.
Deduzca una integral primera del movimiento de la partícula $P\,$ aplicando algún teorema de conservación.

2 Segunda ley de Newton: ecuación de movimiento y tensión del hilo

Sobre la partícula 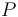$\,P\,$ actúan dos fuerzas: una de naturaleza activa (su peso 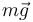$\,m\vec{g}\,$ ) y otra de reacción vincular (la tensión 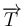$\,\overrightarrow{T}\,$ ejercida por el hilo). La tensión 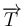$\,\overrightarrow{T}\,$ tiene la dirección del propio hilo (dirección radial) y su sentido es atractivo hacia el extremo fijo $O\,$ (vínculo unilateral). Las expresiones analíticas de las dos fuerzas en la base polar son las siguientes:

$\left\{\begin{array}{l} m\vec{g}=mg\,\vec{\imath}=mg\,[\,\mathrm{cos}(\theta)\,\vec{u}_{\rho}-\mathrm{sen}(\theta)\,\vec{u}_{\theta}\,] \\ \\ \overrightarrow{T}=-T\,\vec{u}_{\rho} \end{array}\right.$

La aceleración de la partícula expresada en la base polar viene dada en general por: 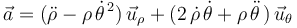$\,\vec{a}=(\ddot{\rho}-\rho\,\dot{\theta}^{\, 2})\,\vec{u}_{\rho}+(2\,\dot{\rho}\,\dot{\theta}+\rho\,\ddot{\theta}\,)\,\vec{u}_{\theta}$ pero al particularizar para la trayectoria circular: 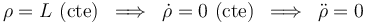$\,\,\rho=L\,\,\mathrm{(cte)}\,\,\,\Longrightarrow\,\,\,\dot{\rho}=0\,\,\mathrm{(cte)}\,\,\,\Longrightarrow\,\,\,\ddot{\rho}=0\,$ , queda: $\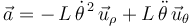vec{a}=-\,L\,\dot{\theta}^{\, 2}\,\vec{u}_{\rho}+L\,\ddot{\theta}\,\vec{u}_{\theta}$

Planteamos la segunda ley de Newton: 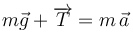$m\vec{g}+\overrightarrow{T}=m\,\vec{a}$ y la proyectamos sobre las direcciones radial y acimutal, obteniendo dos ecuaciones escalares:

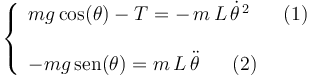
$\left\{\begin{array}{l} mg\,\mathrm{cos}(\theta)-T=-\,m\,L\,\dot{\theta}^{\, 2}\,\,\,\,\,\,\,\,\,\, (1) \\ \\ -mg\,\mathrm{sen}(\theta)=m\,L\,\ddot{\theta}\,\,\,\,\,\,\,\,\,\, (2) \end{array}\right.$

La ecuación (2) nos permite obtener la ecuación diferencial de segundo orden que debe satisfacer la función $\,\theta(t)$ :

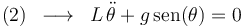
$\mathrm{(2)}\,\,\,\longrightarrow\,\,\,L\,\ddot{\theta}+g\,\mathrm{sen}(\theta)=0$

El módulo 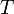$T\,$ de la tensión que ejerce el hilo sobre la partícula se obtiene despejando en la ecuación (1):

$\mathrm{(1)}\,\,\,\longrightarrow\,\,\,T=m\,[L\,\dot{\theta}^{\, 2}+g\,\mathrm{cos}(\theta)]$

3 Integral primera del movimiento: deducción y expresión

La tensión 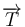$\overrightarrow{T}\,$ no trabaja sobre la partícula por ser siempre perpendicular a su desplazamiento (trayectoria circular). Así que la única fuerza que trabaja sobre la partícula (su peso) es conservativa, y por tanto se conserva constante en el tiempo su energía mecánica 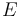$E\,$ (suma de su energía cinética 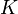$K\,$ y su energía potencial 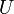$U\,$ ). Dicho de otro modo, el teorema de conservación de la energía mecánica nos permite deducir que 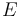$E\,$ es una integral primera del movimiento de la partícula:

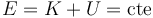
$E=K+U=\mathrm{cte}\,$

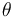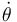Abordemos ahora la tarea de expresar la energía mecánica como una función de $\,\theta\,$ y $\,\dot{\theta}$ .

La velocidad de la partícula expresada en la base polar viene dada en general por:

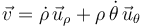
$\vec{v}=\dot{\rho}\,\vec{u}_{\rho}+\rho\,\dot{\theta}\,\vec{u}_{\theta}$

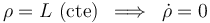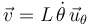
pero al particularizar para la trayectoria circular: $\,\,\rho=L\,\,\mathrm{(cte)}\,\,\,\Longrightarrow\,\,\,\dot{\rho}=0\,$ , queda: $\vec{v}=L\,\dot{\theta}\,\vec{u}_{\theta}$

Así que la energía cinética de la partícula vale:

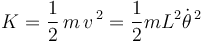
$K=\frac{1}{2}\,m\,v^{\, 2}=\frac{1}{2}mL^2\dot{\theta}^{\, 2}$

Por otra parte, la energía potencial de la partícula es su energía potencial gravitatoria 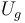$U_g\,$ :

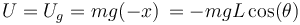
$U=U_g=mg(-x)\,=-mgL\,\mathrm{cos}(\theta)$

Obsérvese que la expresión propuesta para 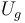$U_g\,$ corresponde a tomar el origen de energía potencial en 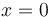$\,x=0\,\,$ , siendo 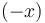$(-x)\,$ la altura de la partícula respecto a dicho origen (nótese que el eje OX apunta hacia abajo).

La suma de energía cinética y energía potencial nos da como resultado la energía mecánica de la partícula:

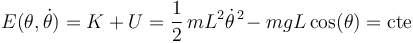
$E(\theta,\dot{\theta})=K+U=\frac{1}{2}\,mL^2\dot{\theta}^{\, 2}\!-mgL\,\mathrm{cos}(\theta)=\mathrm{cte}$

Desde un punto de vista matemático, la integral primera que acabamos de obtener nos proporciona una ecuación diferencial de primer orden que debe ser satisfecha por la función 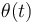$\,\theta(t)$ :

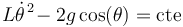
$L\dot{\theta}^{\, 2}\!-2g\,\mathrm{cos}(\theta)=\mathrm{cte}$

Puede comprobarse que, derivando respecto al tiempo esta ecuación diferencial de primer orden (y simplificando), se llega a la ecuación diferencial de segundo orden que se obtuvo a partir de la segunda ley de Newton en el apartado anterior.

@@ Línea 9: / Línea 9: @@
 ==Segunda ley de Newton: ecuación de movimiento y tensión del hilo==
-Sobre la partícula <math>\,P\,</math> actúan dos fuerzas: una de naturaleza activa (su peso <math>\,m\vec{g}\,</math>) y otra de reacción vincular (la tensión <math>\,\overrightarrow{T}\,</math> ejercida por el hilo). La tensión <math>\,\vec{T}\,</math> tiene la dirección del propio hilo (dirección radial) y su sentido es atractivo hacia el extremo fijo <math>O\,</math> (vínculo unilateral). Las expresiones analíticas de las dos fuerzas en la base polar son las siguientes:
+Sobre la partícula <math>\,P\,</math> actúan dos fuerzas: una de naturaleza activa (su peso <math>\,m\vec{g}\,</math>) y otra de reacción vincular (la tensión <math>\,\overrightarrow{T}\,</math> ejercida por el hilo). La tensión <math>\,\overrightarrow{T}\,</math> tiene la dirección del propio hilo (dirección radial) y su sentido es atractivo hacia el extremo fijo <math>O\,</math> (vínculo unilateral). Las expresiones analíticas de las dos fuerzas en la base polar son las siguientes:
 <center><math>
-\left\{\begin{array}{l} m\vec{g}=mg\,\vec{\imath}=mg\,[\,\mathrm{cos}(\theta)\,\vec{u}_{\rho}-\mathrm{sen}(\theta)\,\vec{u}_{\theta}\,] \\ \\ \vec{T}=-T\,\vec{u}_{\rho} \end{array}\right.
+\left\{\begin{array}{l} m\vec{g}=mg\,\vec{\imath}=mg\,[\,\mathrm{cos}(\theta)\,\vec{u}_{\rho}-\mathrm{sen}(\theta)\,\vec{u}_{\theta}\,] \\ \\ \overrightarrow{T}=-T\,\vec{u}_{\rho} \end{array}\right.
 </math></center>
 La aceleración de la partícula expresada en la base polar viene dada en general por:{{qquad}}
@@ Línea 17: / Línea 17: @@
 \,\vec{a}=(\ddot{\rho}-\rho\,\dot{\theta}^{\, 2})\,\vec{u}_{\rho}+(2\,\dot{\rho}\,\dot{\theta}+\rho\,\ddot{\theta}\,)\,\vec{u}_{\theta}
 </math>
 pero al particularizar para la trayectoria circular: {{qquad}} <math>\,\,\rho=L\,\,\mathrm{(cte)}\,\,\,\Longrightarrow\,\,\,\dot{\rho}=0\,\,\mathrm{(cte)}\,\,\,\Longrightarrow\,\,\,\ddot{\rho}=0\,</math>,{{qquad}} queda:{{qquad}}
 <math>
@@ Línea 23: / Línea 22: @@
 </math>
-Planteamos la segunda ley de Newton:{{qquad}} <math>m\vec{g}+\vec{T}=m\,\vec{a}</math>{{qquad}} y la proyectamos sobre las direcciones radial y acimutal, obteniendo dos ecuaciones escalares:
+Planteamos la segunda ley de Newton:{{qquad}} <math>m\vec{g}+\overrightarrow{T}=m\,\vec{a}</math>{{qquad}} y la proyectamos sobre las direcciones radial y acimutal, obteniendo dos ecuaciones escalares:
 <center><math>
 \left\{\begin{array}{l} mg\,\mathrm{cos}(\theta)-T=-\,m\,L\,\dot{\theta}^{\, 2}\,\,\,\,\,\,\,\,\,\, (1) \\ \\
@@ Línea 41: / Línea 40: @@
 ==Integral primera del movimiento: deducción y expresión==
-La tensión <math>\vec{T}\,</math> no trabaja sobre la partícula por ser siempre perpendicular a su desplazamiento (trayectoria circular). Así que la única fuerza que trabaja sobre la partícula (el peso) es conservativa, y por tanto se conserva constante en el tiempo su energía mecánica <math>E\,</math> (suma de su energía cinética <math>K\,</math> y su energía potencial <math>U\,</math>). Dicho de otro modo, el teorema de conservación de la energía mecánica nos ha permitido deducir que <math>E\,</math> es una integral primera del movimiento de la partícula.
+La tensión <math>\overrightarrow{T}\,</math> no trabaja sobre la partícula por ser siempre perpendicular a su desplazamiento (trayectoria circular). Así que la única fuerza que trabaja sobre la partícula (su peso) es conservativa, y por tanto se conserva constante en el tiempo su energía mecánica <math>E\,</math> (suma de su energía cinética <math>K\,</math> y su energía potencial <math>U\,</math>). Dicho de otro modo, el teorema de conservación de la energía mecánica nos permite deducir que <math>E\,</math> es una integral primera del movimiento de la partícula:
+<center><math>E=K+U=\mathrm{cte}\,</math></center>
 Abordemos ahora la tarea de expresar la energía mecánica como una función de <math>\,\theta\,</math> y <math>\,\dot{\theta}</math>.
@@ Línea 60: / Línea 60: @@
 </math></center>
-Por otra parte, la energía potencial de la partícula es la energía potencial gravitatoria <math>U_g\,</math>:
+Por otra parte, la energía potencial de la partícula es su energía potencial gravitatoria <math>U_g\,</math>:
 <center><math>
 U=U_g=mg(-x)\,=-mgL\,\mathrm{cos}(\theta)
 </math></center>
-Obsérvese que la expresión propuesta para <math>U_g\,</math> corresponde a tomar su origen en <math>\,x=0\,\,</math>, siendo <math>(-x)\,</math> la altura de la partícula respecto a dicho origen (nótese que el eje OX apunta hacia abajo).
+Obsérvese que la expresión propuesta para <math>U_g\,</math> corresponde a tomar el origen de energía potencial en <math>\,x=0\,\,</math>, siendo <math>(-x)\,</math> la altura de la partícula respecto a dicho origen (nótese que el eje OX apunta hacia abajo).
 La suma de energía cinética y energía potencial nos da como resultado la energía mecánica de la partícula:
 <center><math>
-E(\theta,\dot{\theta})=K+U=\frac{1}{2}\,mL^2\dot{\theta}^{\, 2}-mgL\,\mathrm{cos}(\theta)=\mathrm{cte}
+E(\theta,\dot{\theta})=K+U=\frac{1}{2}\,mL^2\dot{\theta}^{\, 2}\!-mgL\,\mathrm{cos}(\theta)=\mathrm{cte}
 </math></center>
-Nótese que, desde un punto de vista matemático, la integral primera que acabamos de obtener nos proporciona una ecuación diferencial de primer orden que debe ser satisfecha por la función <math>\,\theta(t)</math>:
+Desde un punto de vista matemático, la integral primera que acabamos de obtener nos proporciona una ecuación diferencial de primer orden que debe ser satisfecha por la función <math>\,\theta(t)</math>:
 <center><math>
 L\dot{\theta}^{\, 2}\!-2g\,\mathrm{cos}(\theta)=\mathrm{cte}

No Boletín - Péndulo simple (Ex.Ene/18)

De Laplace

última version al 16:49 22 feb 2018

1 Enunciado

2 Segunda ley de Newton: ecuación de movimiento y tensión del hilo

3 Integral primera del movimiento: deducción y expresión

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES