Primera Convocatoria Ordinaria 2017/18 (G.I.E.R.M.)
De Laplace
(Página creada con '== Péndulo cónico== right Una masa <math>m</math> cuelga de un hilo tenso, inexten…') |
(→Péndulo cónico) |
||
| Línea 10: | Línea 10: | ||
#Aplicando la Segunda Ley de Newton, determina la relación entre la rapidez de la partícula y el ángulo <math>\alpha</math> que forma el hilo con la vertical. | #Aplicando la Segunda Ley de Newton, determina la relación entre la rapidez de la partícula y el ángulo <math>\alpha</math> que forma el hilo con la vertical. | ||
#Suponiendo que <math>\alpha=\pi/4</math>, y que la dirección de la velocidad apunta en el sentido negativo del eje <math>Z</math>, calcula el momento angular de la partícula respecto al punto <math>O</math> en el instante que se muestra en la figura, así como su derivada temporal. | #Suponiendo que <math>\alpha=\pi/4</math>, y que la dirección de la velocidad apunta en el sentido negativo del eje <math>Z</math>, calcula el momento angular de la partícula respecto al punto <math>O</math> en el instante que se muestra en la figura, así como su derivada temporal. | ||
| + | |||
| + | ==[[Manivela y biela alargada, Enero 2018 (G.I.E.R.M.)| Manivela y biela alargada]]== | ||
| + | [[Imagen:F1GIERM_manivelabiela_enunciado.png|right]] | ||
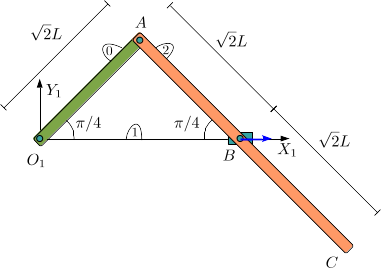
| + | Una barra homogénea (sólido "0") de longitud <math>\sqrt{2}L</math> tiene un extremo articulado en el | ||
| + | punto fijo <math>O</math>. En el otro extremo, <math>A</math>, se articula otra barra homogénea de longitud | ||
| + | <math>2\sqrt{2}L</math> (sólido "2"). El punto medio de esta barra se articula a su vez en un pasador | ||
| + | (punto <math>B</math>), de modo que este punto de la barra se mueve sobre el eje <math>O_1X_1</math>. La barra ``0'' | ||
| + | gira alrededor del eje <math>O_1Z_1</math> con velocidad angular uniforme <math>\Omega</math>. | ||
| + | Todas las magnitudes físicas que se piden | ||
| + | corresponden al instante que se muestra en la figura. | ||
| + | #Localiza gráfica y analíticamente los C.I.R. de los tres movimientos relativos que se pueden definir en el sistema. | ||
| + | #Encuentra reducciones cinemáticas de los tres movimientos relativos. Calcula <math>\vec{v}^{\,C}_{21}</math>. | ||
| + | #Calcula la derivada temporal de la reducción cinemática del movimiento {21} en el punto <math>B</math>. | ||
Revisión de 14:08 7 feb 2018
1 Péndulo cónico
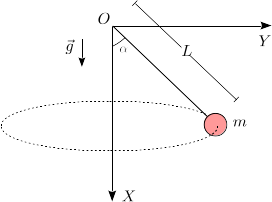
Una masa m cuelga de un hilo tenso, inextensible y sin masa, de longitud L. La masa se mueve de modo que describe un movimiento circular uniforme en torno al eje X, como se indica en la figura. La masa está también sometida a la acción de la gravedad. En el instante mostrado en la figura la partícula está en el plano OXY.
- Dibuja el diagrama de cuerpo libre de la masa. Añade a este diagrama el vector aceleración de la partícula. ¿Cuanto vale el radio de la circunferencia que describe la partícula?
- Aplicando la Segunda Ley de Newton, determina la relación entre la rapidez de la partícula y el ángulo α que forma el hilo con la vertical.
- Suponiendo que α = π / 4, y que la dirección de la velocidad apunta en el sentido negativo del eje Z, calcula el momento angular de la partícula respecto al punto O en el instante que se muestra en la figura, así como su derivada temporal.
2 Manivela y biela alargada
Una barra homogénea (sólido "0") de longitud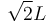 
tiene un extremo articulado en el
punto fijo O. En el otro extremo, A, se articula otra barra homogénea de longitud
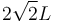(sólido "2"). El punto medio de esta barra se articula a su vez en un pasador
(punto B), de modo que este punto de la barra se mueve sobre el eje O1X1. La barra ``0
gira alrededor del eje O1Z1 con velocidad angular uniforme Ω.
Todas las magnitudes físicas que se piden
corresponden al instante que se muestra en la figura.
- Localiza gráfica y analíticamente los C.I.R. de los tres movimientos relativos que se pueden definir en el sistema.
- Encuentra reducciones cinemáticas de los tres movimientos relativos. Calcula
.
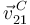- Calcula la derivada temporal de la reducción cinemática del movimiento {21} en el punto B.
