Problemas de dinámica del sólido rígido (CMR)
De Laplace
(Diferencias entre revisiones)
(→Péndulo compuesto) |
(→Péndulo compuesto) |
||
| Línea 1: | Línea 1: | ||
| + | ==[[Momento de inercia de sólidos esféricos]]== | ||
| + | Calcule el momento de inercia de una esfera maciza, de masa ''M'' y radio ''R'' alrededor de de un eje que pasa por su centro. | ||
| + | |||
| + | A partir del resultado anterior, halle el momento de inercia de una esfera hueca, de masa ''M'', radio interior ''R''<sub>1</sub> y exterior ''R''<sub>2</sub> respecto a un eje que pasa por su centro. ¿A qué se reduce el resultado cuando la corona se reduce a una superficie esférica de radio ''R''? | ||
| + | |||
==[[Péndulo compuesto (CMR)|Péndulo compuesto]]== | ==[[Péndulo compuesto (CMR)|Péndulo compuesto]]== | ||
Una barra homogénea de 1kg de masa y 1m de longitud está suspendida del techo por dos soportes muy ligeros, uno de ellos está articulado a un punto A, situado a 20cm de un extremo de la barra y el otro está articulado sin rozamiento en el otro extremo O. | Una barra homogénea de 1kg de masa y 1m de longitud está suspendida del techo por dos soportes muy ligeros, uno de ellos está articulado a un punto A, situado a 20cm de un extremo de la barra y el otro está articulado sin rozamiento en el otro extremo O. | ||
Revisión de 12:05 10 ene 2018
1 Momento de inercia de sólidos esféricos
Calcule el momento de inercia de una esfera maciza, de masa M y radio R alrededor de de un eje que pasa por su centro.
A partir del resultado anterior, halle el momento de inercia de una esfera hueca, de masa M, radio interior R1 y exterior R2 respecto a un eje que pasa por su centro. ¿A qué se reduce el resultado cuando la corona se reduce a una superficie esférica de radio R?
2 Péndulo compuesto
Una barra homogénea de 1kg de masa y 1m de longitud está suspendida del techo por dos soportes muy ligeros, uno de ellos está articulado a un punto A, situado a 20cm de un extremo de la barra y el otro está articulado sin rozamiento en el otro extremo O.
- Determine la fuerza que ejerce cada soporte en el equilibrio.
- En un momento dado, se rompe el soporte en A. Justo tras el corte, halle:
- La aceleración lineal del centro de masas de la barra, G.
- La aceleración angular de la barra
- La fuerza que realiza el soporte en O. ¿Cuánto ha aumentado o disminuido respecto a la situación de equilibrio?
- Suponga que la articulación en O es un par de revolución, de forma que solo puede moverse en el plano OXZ
- Obtenga la ecuación de movimiento para el ángulo que forma con la vertical
- Halle las frecuencia de las pequeñas oscilaciones que realiza cuando se suelta desde una posición próxima a la vertical.
- Para el caso del enunciado, que se suelta desde la posición horizontal, calcule la fuerza que ejerce el soporte en O para cada ángulo θ
- Suponga ahora que la articulación en O es una rótula, de forma que la barra puede tanto variar su ángulo θ con la vertical como el ángulo φ alrededor de OZ.
- Determine las ecuaciones de movimiento para estos dos ángulos.
- Halle dos constantes de movimiento no triviales.
- Con ayuda de las constantes anteriores, halle una ecuación de movimiento para θ que no incluya a φ
- Calcule qué valor debe tener la velocidad angular
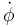para la que la barra gire en torno a OZ manteniendo constante su ángulo θ con la vertical.
