Problemas de mecánica analítica (CMR)
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Péndulo compuesto== Para el sistema del problema “Péndulo compuesto” analice e…') |
(→Péndulo compuesto) |
||
| Línea 1: | Línea 1: | ||
| - | ==[[Péndulo compuesto por mecánica analítica (CMR)|Péndulo compuesto]]== | + | ==[[Péndulo compuesto. Análisis por mecánica analítica (CMR)|Péndulo compuesto]]== |
Para el sistema del problema “[[Péndulo compuesto (CMR)|Péndulo compuesto]]” analice el problema general mediante las técnicas de mecánica analítica. Se tiene una barra homogénea de longitud b y masa m, articulada mediante una rótula en un extremo O y sometida a la acción de la gravedad. La barra puede tanto variar su ángulo θ con la vertical como el ángulo ϕ alrededor de OZ. | Para el sistema del problema “[[Péndulo compuesto (CMR)|Péndulo compuesto]]” analice el problema general mediante las técnicas de mecánica analítica. Se tiene una barra homogénea de longitud b y masa m, articulada mediante una rótula en un extremo O y sometida a la acción de la gravedad. La barra puede tanto variar su ángulo θ con la vertical como el ángulo ϕ alrededor de OZ. | ||
Revisión de 23:56 9 ene 2018
Péndulo compuesto
Para el sistema del problema “Péndulo compuesto” analice el problema general mediante las técnicas de mecánica analítica. Se tiene una barra homogénea de longitud b y masa m, articulada mediante una rótula en un extremo O y sometida a la acción de la gravedad. La barra puede tanto variar su ángulo θ con la vertical como el ángulo ϕ alrededor de OZ.
Para este sistema
- Calcule la lagrangiana del sistema.
- Halle las ecuaciones de movimiento para los dos ángulos de giro, θ y ϕ
- Obtenga dos constantes de movimiento no triviales.
- Con ayuda de las constantes de movimiento, halle una ecuación que incluya solamente a θ
- Calcule el valor que debe tener la velocidad angular
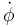si se desea que la barra mantenga una inclinación constante respecto a la vertical.
