Péndulo compuesto. Análisis por mecánica analítica (CMR)
De Laplace
Contenido |
1 Enunciado
Para el sistema del problema “Péndulo compuesto” analice el problema general mediante las técnicas de mecánica analítica. Se tiene una barra homogénea de longitud b y masa m, articulada mediante una rótula en un extremo O y sometida a la acción de la gravedad. La barra puede tanto variar su ángulo θ con la vertical como el ángulo ϕ alrededor de OZ.
Para este sistema
- Calcule la lagrangiana del sistema.
- Halle las ecuaciones de movimiento para los dos ángulos de giro, θ y ϕ
- Obtenga dos constantes de movimiento no triviales.
- Con ayuda de las constantes de movimiento, halle una ecuación que incluya solamente a θ
- Calcule el valor que debe tener la velocidad angular
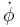 si se desea que la barra mantenga una inclinación constante respecto a la vertical.
si se desea que la barra mantenga una inclinación constante respecto a la vertical.
2 Lagrangiana del sistema
En este sistema no hay fuerzas no conservativas y los vínculos son geométricos (ya que el único vínculo es que el extremo O es un punto fijo). Por ello, las ecuaciones de movimiento pueden obtenerse a partir de las ecuaciones de Lagrange
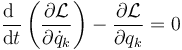
siendo
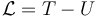
la lagrangiana del sistema. Aquí T = K es la energía cinética y U la potencial.
La energía cinética de un sólido con un punto fijo O se puede calcular como
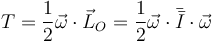
Tal como se ve en el problema citado, la expresión más simple de la energía cinética se obtiene en un sistema de referencia ligado en el que el eje OZ2 va en la dirección de la barra y los otros dos son ortogonales a éste por O. En este sistema la energía cinética tiene la expresión
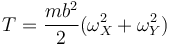
A su vez, como se ve en el mismo problema, las componentes de la velocidad angular en el sistema ligado se relacionan con las derivadas de los ángulos por
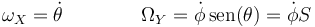
lo que nos da la expresión para la energía cinética
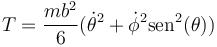
Por su parte, la energía potencial sale de la altura del CM
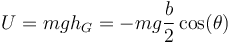
Por tanto la lagrangiana del sistema es
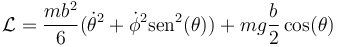
3 Ecuaciones de movimiento
3.1 Para el ángulo ϕ
La ecuación de Lagrange para este ángulo es
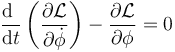
Calculamos en primer lugar el momento conjugado
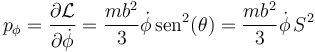
siendo su derivada temporal
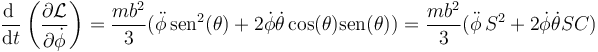
Por otro lado, la lagrangiana no depende explícitamente del ángulo ϕ
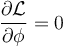
por lo que la ecuación de movimiento buscada es
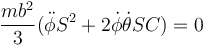
Podemos sacar factores comunes y reducirla a
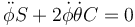
3.2 Para el ángulo θ
De manera análoga operamos con el otro ángulo. Su momento conjugado vale
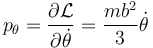
cuya derivada respecto al tiempo es simplemente
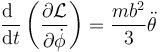
En cuanto a la derivada respecto al ángulo tenemos términos en la energía cinética y en la potencial
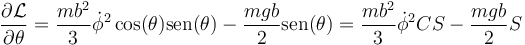
lo que nos da la ecuación de movimiento
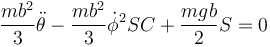
Sacando factores comunes y abreviando la expresión nos queda
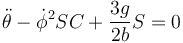
Esta ecuación y la anterior coinciden con las obtenidas en el problema del análisis vectorial de este sistema.
4 Constantes de movimiento
En este problema tenemos dos constantes de movimiento no triviales.
4.1 Coordenada cíclica
Según hemos indicado, la coordenada ϕ no aparece explícitamente en la lagrangiana
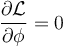
Se dice en este caso que ϕ es cíclica. en este caso, es inmediato que su momento conjugado es una constante de movimiento
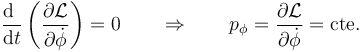
siendo su expresión en este caso
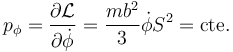
Este término coincide con la componente z del momento cinético. Su constancia está asociada a que el sistema es invariante ante una rotación en torno al eje OZ.
4.2 Independencia del tiempo
La lagrangiana de este sistema no depende del tiempo. Esto implica que la cantidad
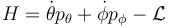
es una constante de movimiento. En este caso, tras sustituir los momentos y operar llegamos a que H coincide con la energía mecánica
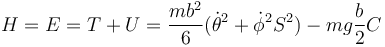
5 Ecuación para θ
Despejando la derivada respecto al tiempo en la primera constante
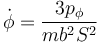
y sustituyendo en la ecuación de movimiento para θ obtenemos una para esta variable exclusivamente
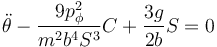
Una manera más formal de llegar a ella es empleando la función de Routh. Aplicando que ϕ es cíclica, definimos la función
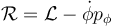
que en este caso vale
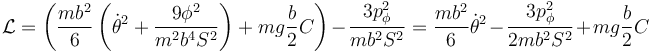
Una vez definida esta función, la ecuación para θ se halla como
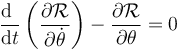
El resultado es el mismo que ya hemos visto.
6 Movimiento con inclinación constante
Si se desea que la barra mantenga constante su inclinación, debe anularse la derivada 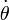 , lo que nos da la condición
, lo que nos da la condición
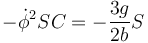
y por tanto
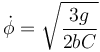
Como el coseno vale como máximo 1, existe una velocidad angular mínima para poder conseguir una inclinación constante.





