Nave espacial alejándose de un planeta (G.I.A.)
De Laplace
(→Impulso mecánico en el instante inicial) |
(→Impulso mecánico en el instante inicial) |
||
| Línea 45: | Línea 45: | ||
<center><math> | <center><math> | ||
| - | \left. \begin{array}{l} \vec{p}\!\ (t=0^-)=m\!\ \vec{v}\!\ (t=0^-)=mv_0\!\ \vec{\jmath}\\ \\ \displaystyle \vec{p}\!\ (t=0^+)=m\!\ \vec{v}\!\ (t=0^+)=m\frac{v_0}{2\pi}\ \bigg[\vec{\imath}+2\pi\vec{\jmath}\bigg]\end{array}\right\} \quad \Longrightarrow | + | \left. \begin{array}{l} \vec{p}\!\ (t=0^-)=m\!\ \vec{v}\!\ (t=0^-)=mv_0\!\ \vec{\jmath}\\ \\ \displaystyle \vec{p}\!\ (t=0^+)=m\!\ \vec{v}\!\ (t=0^+)=m\!\ \frac{v_0}{2\pi}\ \bigg[\vec{\imath}+2\pi\vec{\jmath}\bigg]\end{array}\right\} \quad \Longrightarrow\quad \vec{\mathcal{P}}(t=0)==m\!\ \frac{v_0}{2\pi}\ \vec{\imath} |
</math></center> | </math></center> | ||
Revisión de 19:15 4 ene 2018
1 Enunciado
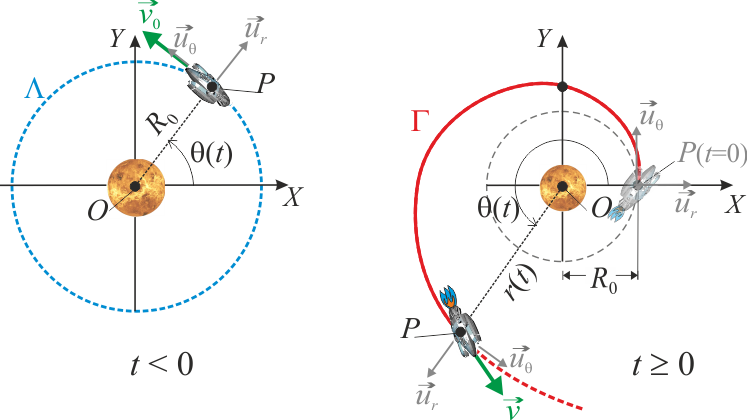
Una nave espacial que --en primera aproximación-- se considerará como partícula material P de masa m constante, se mueve en las proximidades de un planeta de masa M y centro O, sometida a la acción gravitatoria de éste,
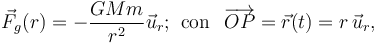
donde 
, es la distancia que separa la nave del
centro O, y G es la constante de gravitación universal.
Con anterioridad al instante que tomaremos como t = 0, la
nave orbita en torno al planeta con los motores apagados, recorriendo
la órbita circular Λ, de radio R0 y centro en O, con velocidad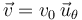 
, siendo su módulo el valor constante 
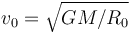. En el instante t = 0, cuando la nave se halla en la posición de Λ correspondiente a θ = 0, los motores se encienden súbitamente. En instantes posteriores, 
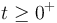, la
nave se aleja del planeta siguiendo la trayectoria espiral Γ,
contenida en el mismo plano OXY que la órbita circular Λ. Además, la nave recorre dicha trayectoria de manera que su momento cinético respecto del origen O permanece constante. Las
expresiones en coordenada polares de la trayectoria Γ y de la
velocidad instantánea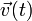 
de la nave cuando recorre dicha
trayectoria son:
![\Gamma: \; \vec{r}(\theta)=r(\theta)\!\ \vec{u}_r\mathrm{,}\quad \mathrm{con}\;\; r(\theta)= \frac{2\pi
R_0}{2\pi-\theta}\mathrm{;}\qquad\vec{v}[\theta(t)]=\frac{v_0}{2\pi}\bigg\{
\vec{u}_r+\bigg[2\pi-\theta(t)\bigg]\vec{u}_\theta\bigg\}](/wiki/images/math/4/0/1/401043e3878d57b596d477b3f3d1f8f5.png)
con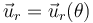 
y
.
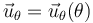- Calcule el impulso mecánico instantáneo
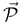(percusión) ejercido por los motores al encenderse de forma súbita en el instante t = 0, para que la nave inicie la maniobra de alejamiento a partir de t = 0 + .
- Obtenga la expresión de la energía mecánica de la nave en función del tiempo, E(t), antes y después de ponerse en marcha los motores.
- Obtenga la potencia desarrollada por los motores cuando la nave recorre la trayectoria espiral $\Gamma$, expresada en función de la posición. Demuestre que dicha potencia alcanza su valor máximo en la posición correspondiente a r = 3R0 / 2. ¿Qué trabajo han de realizar los motores para llegar a dicho punto?
2 Solución
2.1 Impulso mecánico en el instante inicial
El impulso mecánico instantáneo (percusión) ejercido por los motores en el instante inicial t = 0, es igual a la variación instantánea de la cantidad de movimiento de la nave:
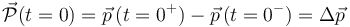
Antes de encenderse los motores (es decir, para t < 0), la nave realiza un movimiento circular uniforme con celeridad de valor conocido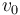 
. En el considerado como instante inicial, cuando θ(t = 0) = 0, se tendrá que 
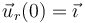, y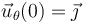 
. Entonces,
![\left. \begin{array}{l} \vec{p}\!\ (t=0^-)=m\!\ \vec{v}\!\ (t=0^-)=mv_0\!\ \vec{\jmath}\\ \\ \displaystyle \vec{p}\!\ (t=0^+)=m\!\ \vec{v}\!\ (t=0^+)=m\!\ \frac{v_0}{2\pi}\ \bigg[\vec{\imath}+2\pi\vec{\jmath}\bigg]\end{array}\right\} \quad \Longrightarrow\quad \vec{\mathcal{P}}(t=0)==m\!\ \frac{v_0}{2\pi}\ \vec{\imath}](/wiki/images/math/f/f/2/ff290b80f578917084e49bdd05eb9cab.png)
