Nave espacial alejándose de un planeta (G.I.A.)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

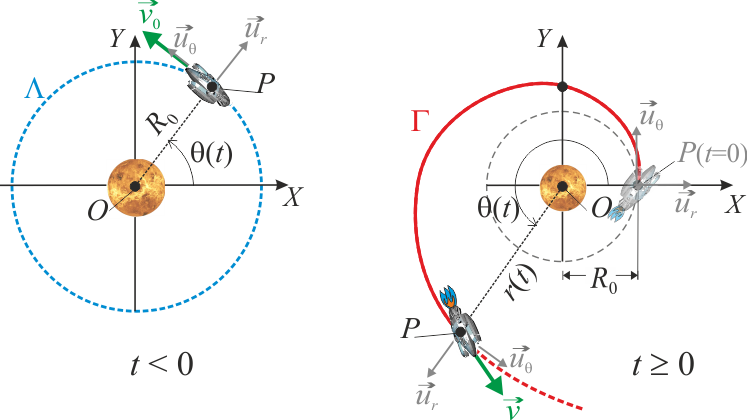
Una nave espacial que --en primera aproximación-- se considerará como partícula material $P$ de masa $m$ constante, se mueve en las proximidades de un planeta de masa $M$ y centro $O$ , sometida a la acción gravitatoria de éste,

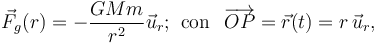
$\vec{F}_g(r)=-\frac{GMm}{r^2}\vec{u}_r\mathrm{;} \;\;\mathrm{con}\,\;\; \overrightarrow{OP}=\vec{r}(t)=r\!\ \vec{u}_r\mathrm{,}$

donde $r=|\vec{r}|$ , es la distancia que separa la nave del centro $O$ , y $G$ es la constante de gravitación universal.

Con anterioridad al instante que tomaremos como $t = 0$ , la nave orbita en torno al planeta con los motores apagados, recorriendo la órbita circular $Λ$ , de radio $R 0$ y centro en $O$ , con velocidad 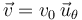$\vec{v}=v_0\!\ \vec{u}_\theta$ , siendo su módulo el valor constante 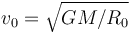$\, v_0=\sqrt{GM/R_0}$ . En el instante $t = 0$ , cuando la nave se halla en la posición de $Λ$ correspondiente a $θ = 0$ , los motores se encienden súbitamente. En instantes posteriores, 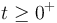$t\geq 0^+$ , la nave se aleja del planeta siguiendo la trayectoria espiral $Γ$ , contenida en el mismo plano $O X Y$ que la órbita circular $Λ$ . Además, la nave recorre dicha trayectoria de manera que su momento cinético respecto del origen $O$ permanece constante. 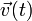Las expresiones en coordenada polares de la trayectoria $Γ$ y de la velocidad instantánea $\vec{v}(t)$ de la nave cuando recorre dicha trayectoria son:

$\Gamma: \; \vec{r}(\theta)=r(\theta)\!\ \vec{u}_r\mathrm{,}\quad \mathrm{con}\;\; r(\theta)= \frac{2\pi R_0}{2\pi-\theta}\mathrm{;}\qquad\vec{v}[\theta(t)]=\frac{v_0}{2\pi}\bigg\{ \vec{u}_r+\bigg[2\pi-\theta(t)\bigg]\vec{u}_\theta\bigg\}$

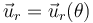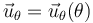con $\vec{u}_r=\vec{u}_r(\theta)\,$ y $\,\vec{u}_\theta=\vec{u}_\theta(\theta)$ .

Calcule el impulso mecánico instantáneo 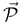$\vec{\mathcal{P}}$ (percusión) ejercido por los motores al encenderse de forma súbita en el instante $t = 0$ , para que la nave inicie la maniobra de alejamiento a partir de $t = 0 +$ .
Obtenga la expresión de la energía mecánica de la nave en función del tiempo, $E (t)$ , antes y después de ponerse en marcha los motores.
Obtenga la potencia desarrollada por los motores cuando la nave recorre la trayectoria espiral $Γ$ , expresada en función de la posición. Demuestre que dicha potencia alcanza su valor máximo en la posición correspondiente a $r = 3 R 0 / 2$ . ¿Qué trabajo han de realizar los motores para llegar a dicho punto?

2 Solución

2.1 Impulso mecánico en el instante inicial

El impulso mecánico instantáneo (percusión) ejercido por los motores en el instante inicial $t = 0$ , es igual a la variación instantánea de la cantidad de movimiento de la nave:

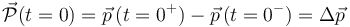
$\vec{\mathcal{P}}(t=0)=\vec{p}\!\ (t=0^+)-\vec{p}\!\ (t=0^-)=\Delta\vec{p}$

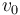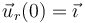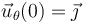Antes de encenderse los motores (es decir, para $t < 0$ ), la nave realiza un movimiento circular uniforme con celeridad de valor conocido $\, v_0$ . En el considerado como instante inicial, cuando $θ(t = 0) = 0$ , se tendrá que $\vec{u}_r(0)=\vec{\imath}$ , y $\, \vec{u}_\theta(0)=\vec{\jmath}$ . Entonces,

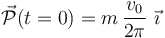
$\left. \begin{array}{l} \vec{p}\!\ (t=0^-)=m\!\ \vec{v}\!\ (t=0^-)=mv_0\!\ \vec{\jmath}\\ \\ \displaystyle \vec{p}\!\ (t=0^+)=m\!\ \vec{v}\!\ (t=0^+)=m\!\ \frac{v_0}{2\pi}\ \bigg[\vec{\imath}+2\pi\vec{\jmath}\bigg]\end{array}\right\} \quad \Longrightarrow\quad$ $\vec{\mathcal{P}}(t=0)=m\!\ \frac{v_0}{2\pi}\ \vec{\imath}$

2.2 Energía mecánica de la nave

La energía mecánica en cada instante es igual a la suma de la energía cinética más la energía potencial total, asociada a la(s) fuerza(s) conservativa(s) que actúa(n) sobre la partícula. En el caso de la nave/partícula bajo estudio, de masa $m$ , hay una única fuerza conservativa: la de interacción gravitatoria 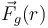$\vec{F}_g(r)$ . Como se sabe, la energia potencial gravitatoria $U g (r)$ asociada a dicha fuerza es tal que...

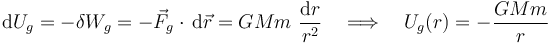
$\mathrm{d}U_g=-\delta W_g=-\vec{F}_g\cdot\,\mathrm{d}\vec{r}=GMm\ \frac{\mathrm{d}r}{r^2}\quad \Longrightarrow\quad U_g(r)=-\frac{GMm}{r}$

de manera que 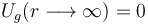$U_g(r\longrightarrow\infty)=0$ .

En instantes anteriores, cuando la nave recorre una órbita circular en torno al planeta, manteniéndose a una distancia $r = R 0$ de su centro, y a una velocidad de módulo constante $v 0$ , se tendrá...

$\left. \begin{array}{l}\displaystyle K(t<0)=\frac{1}{2}\ m\!\ |\vec{v}|^2=\frac{1}{2}\ m\!\ v_0^2=\frac{mGM}{2\!\ R_0}\\ \\ \displaystyle U_g[r(t<0)]=-\frac{GMm}{R_0}\end{array}\right\}\quad \Longrightarrow\quad$ $E(t<0)=K(t<0)+U_g[r(t<0)]=-\frac{GMm}{2\!\ R_0}\ \,\mathrm{,}\;\;\,\mathrm{cte.}\,\,$

Obsérvese que, como para $t < 0$ , la nave realiza un movimiento circular uniforme con centro en el punto $O$ (centro del planeta), las energías cinética y potencial de la nave, tienen ambas valores constantes. Por tanto, la energía mecánica de la nave antes de encenderse los motores, tiene también un valor constante.

Tras encenderse los motores (para $t > 0$ ) la velocidad, y por tanto, la energía cinética, dejan de ser constantes. Teniendo en cuenta la ecuación de la trayectoria $Γ$ , la expresiones de estas magnitudes en función de la posición (dada por el valor de $θ$ o de $r$ ), son:

$\vec{v}(t>0)=\frac{v_0}{2\pi}\ \big\{\vec{u}_r+\big[2\pi-\theta(t)\big]\vec{u}_\theta\big\}=\frac{v_0}{2\pi}\ \left[\vec{u}_r+\frac{2\pi\!\ R_0}{r(t)}\ \vec{u}_\theta\right]\quad\Longrightarrow\quad K(t>0)=\frac{1}{2}\ m\!\ \frac{v_0^2}{4\pi^2}\ \left[1+\frac{4\pi^2\!\ R_0^2}{r^2(t)}\right]=\frac{GMm}{2\!\ R_0}\ \left[\frac{1}{4\pi^2}+\frac{R_0^2}{r^2(t)}\right]$

Por otra parte, cuando la nave recorre la trayectoria $Γ$ , la energía potencial gravitatoria de la nave, en función de la distancia $r (t)$ a que se encuentra del centro $O$ del planeta, es...

$U_g[r(t>0)]=-\frac{GMm}{r(t)}$

... que sumada a la energía cinética, proporciona la expresión de la energía mecánica de la nave para instantes $t > 0$ :

$E(t>0)=K(t>0)+U_g[r(t>0)]=\frac{GMm}{2\!\ R_0}\ \left[\frac{1}{4\pi^2}-\frac{2\!\ R_0}{r(t)}+\frac{R_0^2}{r^2(t)}\right]=E(t)$

2.3 Potencia de los motores

La potencia desarrollada por los motores mientras la nave realiza la maniobra de alejamiento, puede obtenerse por diversos procedimientos. Por ejemplo, a partir del teorema de las fuerzas vivas, se tendrá que la variación instantánea de energía cinética es igual a la suma de los trabajos elementales de las fuerzas que actúan sobre la nave: es decir, el trabajo realizado por la fuerza gravitatoria, $δ W g = - d U g$ , y el trabajo “no conservativo” realizado por los motores 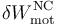$\delta W_\mathrm{mot}^\mathrm{NC}$ . A partir de este resultado, se obtiene que la variación de la energía mecánica de la nave/partícula es igual al trabajo relizado por fuerza no conservativa que ejercen los motores. En un $d t$ , se tendrá:

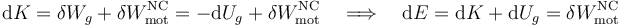
$\mathrm{d}K=\delta W_g+\delta W_\mathrm{mot}^\mathrm{NC}=-\mathrm{d}U_g+\delta W_\mathrm{mot}^\mathrm{NC}\quad\Longrightarrow\quad \mathrm{d}E=\mathrm{d}K+\mathrm{d}U_g=\delta W_\mathrm{mot}^\mathrm{NC}$

En consecuencia, la potencia (trabajo por unidad de tiempo) desarrollada por aquéllos, será igual a la variación que por unidad de tiempo verifica la energía mecánica:

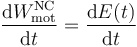
$\frac{\mathrm{d}W_\mathrm{mot}^\mathrm{NC}}{\mathrm{d}t}=\frac{\mathrm{d}E(t)}{\mathrm{d}t}$

A partir de la expresión obtenida anteriormente para la energía mecánica en función de la posición, dada por $r (t)$ ...

$\frac{\mathrm{d}W_\mathrm{mot}^\mathrm{NC}}{\mathrm{d}t}=\frac{\mathrm{d}E}{\mathrm{d}r}\!\ \frac{\mathrm{d}r}{\mathrm{d}t}=\frac{GMm}{2\!\ R_0}\!\ \left[\frac{2\!\ R_0}{r^2(t)}- \frac{2\!\ R_0^2}{r^3(t)}\right]\!\ \dot{r}(t)\!\$

... y para determinar 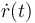$\dot{r}(t)$ , basta con identificar este término en la expresión de la velocidad de la partícula en polares para instantes $t > 0$ :

$\vec{v}(t>0)=\frac{v_0}{2\pi}\ \left[\vec{u}_r+\frac{2\pi\!\ R_0}{r(t)}\ \vec{u}_\theta\right]=\dot{r}(t)\!\ \vec{u}_r+ r(t)\dot{\theta}(t)\vec{u}_\theta\quad \Longrightarrow\quad \left\{\begin{array}{l} \displaystyle\dot{r}(t)=\frac{v_0}{2\pi}\\ \\ \displaystyle \dot\theta (t)=\frac{v_0\!\ R_0}{r^2(t)}\end{array}\right.$

Por tanto, la potencia que desarrollan los motores en un determinado instante, cuando la nave se halla a una distancia $r (t)$ del centro $O$ , es:

$\frac{\mathrm{d}W_\mathrm{mot}^\mathrm{NC}}{\mathrm{d}t}=\frac{GMm\!\ v_0}{2\!\ \pi}\!\ \left[\frac{1}{r^2(t)}- \frac{R_0}{r^3(t)}\right]=\mathrm{P}_\mathrm{mot}[r(t)]$

Para determinar en qué punto de la trayectoria $Γ$ , dicha potencia alcanza un valor máximo, exigimos que se anule la derivada primera con respecto a la distancia $r$ ,...

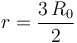
$\frac{\mathrm{d}\mathrm{P}_\mathrm{mot}}{\mathrm{d}r}=\frac{GMm\!\ v_0}{2\!\ \pi}\!\ \left[-\frac{2}{r^3}+ \frac{3\!\ R_0}{r^4}\right]=0\quad \Longleftrightarrow\quad$ $r=\frac{3\!\ R_0}{2}$

... y comprobamos que la derivada segunda sea negativa en dicho punto:

$\frac{\mathrm{d}^2\mathrm{P}_\mathrm{mot}}{\mathrm{d}r^2}=\frac{GMm\!\ v_0}{2\!\ \pi}\!\ \left[\frac{6}{r^4}- \frac{12\!\ R_0}{r^5}\right]\quad \Longrightarrow\quad\frac{\mathrm{d}^2\mathrm{P}_\mathrm{mot}}{\mathrm{d}r^2}\bigg\rfloor_{r=3R_0/2}<0$

Sea $t M$ el instante en que la nave alcanza la posición donde la potencia desarrollada por los motores es máxima,

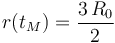
$r(t_M)=\frac{3\!\ R_0}{2}$

El trabajo total realizado por éstos para sacar a la nave/partícula de la trayectoria circular $Λ$ , y llevarla hasta dicha posición sería igual a la variación de la energía mécanica de la nave:

$W_\mathrm{mot}^\mathrm{NC}=E(t_M)-E(t=0^-)=\frac{GMm}{2\!\ R_0}\!\ \left[\frac{1}{4\pi^2}+\frac{1}{9}\right]$

Por otra parte, y aunque no es necesario para la resolución de las cuestiones planteadas en el ejercicio, es posible obtener la ley horaria $r = r (t)$ que describe el movimiento de la nave/partícula a lo largo de la trayectoria $Γ$ . Como hemos determinado la derivada temporal de dicha ley, $d o t r (t)$ , y se conoce su valor en el instante inicial...

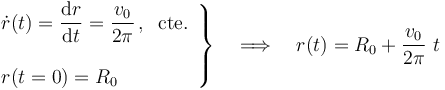
$\left.\begin{array}{l} \displaystyle \dot{r}(t)=\frac{\mathrm{d}r}{\mathrm{d}t}=\frac{v_0}{2\pi}\,\mathrm{,}\,\;\;\mathrm{cte.}\\ \\ \displaystyle r(t=0)=R_0\end{array}\right\} \quad\Longrightarrow\quad r(t)=R_0+\frac{v_0}{2\pi}\ t$

2.3.1 Otro procedimiento para calcular la potencia de los motores

Como sabemos, si 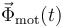$\vec{\Phi}_\mathrm{mot}(t)$ es la fuerza (no conservativa) que ejercen los motores en el instante $t$ , la potencia instantánea que ejercen sobre la nave/partícula es...

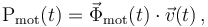
$\mathrm{P}_\mathrm{mot}(t)=\vec{\Phi}_\mathrm{mot}(t)\cdot \vec{v}(t)\,\mathrm{,}\,$

donde 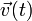$\vec{v}(t)$ es la velocidad instantánea de dicha nave. Para obtener la expresión de la fuerza de los motores, podemos aplicar las leyes de la Dinámica. Es decir, la fuerza resultante 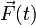$\vec{F}(t)$ que actúa sobre la partícula (ejercida por los motores y por el planeta próximo) es igual a la variación por unidad de tiempo de su cantidad de movimiento. Y como se asume que los motores de la nave utilizan una sofisticada tecnología que hace que la masa de la nave no cambie, dicha variación de la cantidad de movimiento será igual a la masa por la aceleración instantantánea. Por tanto.

$\vec{F}(t)=\vec{\Phi}_\mathrm{mot}+ \vec{F}_g=m\!\ \frac{\mathrm{d}\vec{v}}{\mathrm{d}t}\quad \Longrightarrow\quad \vec{\Phi}_\mathrm{mot}= m\!\ \vec{a}(t)-\vec{F}_g[\vec{r}(t)]$

Para calcular la aceleración instantánea de la partícula bastaría con derivar con respecto al tiempo la expresión conocida de la velocidad, teniendo en cuenta que

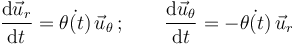
$\frac{\mathrm{d}\vec{u}_r}{\mathrm{d}t}=\dot{\theta(t)}\!\ \vec{u}_{\theta}\,\mathrm{;}\,\quad\quad\frac{\mathrm{d}\vec{u}_\theta}{\mathrm{d}t}=-\dot{\theta(t)}\!\ \vec{u}_r$

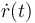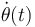... y que $\dot{r}(t)$ y $\dot{\theta}(t)$ son funciones conocidas.

Pero podemos ahorrar algo de cálculo si aplicamos el dato indicado en el enunciado de que, durante el movimiento, el momento cinético de la nave/partícula respecto del punto $O$ , permanece constante. Aplicamos entonces el teorema de conservación del momento cinético...

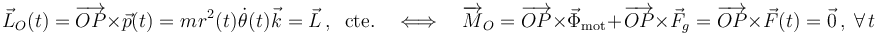
$\vec{L}_O(t)=\overrightarrow{OP}\times \vec{p}(t)=m\!\ r^2(t)\!\ \dot{\theta}(t)\!\ \vec{k}=\vec{L}\,\mathrm{,}\,\;\;\mathrm{cte.}\quad\Longleftrightarrow\quad \overrightarrow{M}_O=\overrightarrow{OP}\times \vec{\Phi}_\mathrm{mot}\!\ +\!\ \overrightarrow{OP}\times \vec{F}_g=\overrightarrow{OP}\times \vec{F}(t)=\vec{0}\,\mathrm{,}\,\;\forall\, t$

Es decir, la fuerza resultante que actúa sobre la partícula debe ser, en general, una fuerza central con centro en el punto fijo $O$ . En consecuencia, la aceleración de la nave, expresada en coordenadas polares, sólo debe tener componente radial:

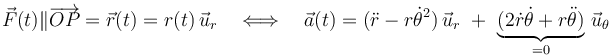
$\vec{F}(t)\|\overrightarrow{OP}=\vec{r}(t)=r(t)\!\ \vec{u}_r\quad\Longleftrightarrow\quad \vec{a}(t)=\big(\ddot{r}-r\dot{\theta}^2\big)\!\ \vec{u}_r\ + \ \underbrace{\big(2\dot{r}\dot{\theta}+r\ddot{\theta}\big)}_{=0}\!\ \vec{u}_\theta$

Utilizando la expresión obtenida anteriormente para 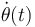$\dot{\theta}(t)$ , y teniendo en cuenta que 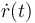$\dot{r}(t)$ es constante en el tiempo y, por tanto, 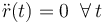$\ddot{r}(t)=0\;\; \forall\, t$ , se obtiene...

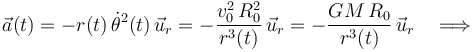
$\vec{a}(t)=-r(t)\!\ \dot{\theta}^2 (t)\!\ \vec{u}_r=-\frac{v_0^2\!\ R_0^2}{r^3(t)}\!\ \vec{u}_r=-\frac{GM\!\ R_0}{r^3(t)}\!\ \vec{u}_r \quad\Longrightarrow\quad$ $\vec{\Phi}_\mathrm{mot}= m\!\ \vec{a}(t)-\vec{F}_g[\vec{r}(t)] =GMm\!\ \left[\frac{1}{r^2(t)}-\frac{R_0}{r^3(t)}\right]\!\ \vec{u}_r$

... y calculando su producto escalar por la velocidad instantánea de la partícula, obtenemos la potencia instantánea de los motores:

$\mathrm{P}_\mathrm{mot}(t)=\vec{\Phi}_\mathrm{mot}(t)\cdot \vec{v}(t)=\frac{GMm\!\ v_0}{2\!\ \pi}\!\ \left[\frac{1}{r^2(t)}- \frac{R_0}{r^3(t)}\right]$

Nave espacial alejándose de un planeta (G.I.A.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Impulso mecánico en el instante inicial

2.2 Energía mecánica de la nave

2.3 Potencia de los motores

2.3.1 Otro procedimiento para calcular la potencia de los motores

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES