Dos masas unidas por un muelle
De Laplace
(Página creada con '==Enunciado== Dos masas <math>m_1</math> y <math>m_2</math> se mueven a lo largo del eje OX unidas por un resorte de constante <math>k</math> y longitud natura <math>\ell_0</mat…') |
|||
| Línea 6: | Línea 6: | ||
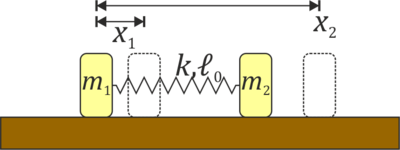
<center>[[Archivo:dos-masas-muelle-horizontal.png|400px]]</center> | <center>[[Archivo:dos-masas-muelle-horizontal.png|400px]]</center> | ||
==Ecuaciones de movimiento== | ==Ecuaciones de movimiento== | ||
| + | Las dos masas describen un movimiento rectilíneo, por lo que podemos emplear cantidades escalares, en lugar de vectores. | ||
| + | |||
| + | En ese caso, la segunda ley de Newton aplicada a cada partícula nos da | ||
| + | |||
| + | <center><math>m_1\ddot{x}_1 = F_1\qquad\qquad m_2\ddot{x}_2 = F_2</math></center> | ||
| + | |||
| + | La fuerza que actúa sobre cada partícula es la debida al resorte (aparte estarían el peso y la normal, pero se cancelan mutuamente, por lo que no influyen). Esta fuerza está gobernada por la ley de Hooke | ||
| + | |||
| + | <center><math>F_1= k(x_2-x_1-\ell_0)\qquad\qquad F_2=-k(x_2-x_1-\ell_0)</math></center> | ||
| + | |||
| + | donde el signo es tal que si el muelle está estirado tiende a reunir las dos masas. | ||
| + | |||
| + | Por tanto, tenemos el sistema de ecuaciones diferenciales | ||
| + | |||
| + | <center><math>\begin{array}{rcl} | ||
| + | m_1 \ddot{x}_1 & = & k(x_2-x_1-\ell_0) \\ | ||
| + | m_2 \ddot{x}_2 & = & -k(x_2-x_1-\ell_0) | ||
| + | \end{array}</math></center> | ||
| + | |||
| + | con las condiciones iniciales, en este caso | ||
| + | |||
| + | <center><math>x_{10}=0\qquad\qquad\dot{x}_{10}=v_0\qquad\qquad x_{20}=\ell_0\qquad\qquad\dot{x}_{20}=0</math></center> | ||
| + | |||
==Constantes de movimiento== | ==Constantes de movimiento== | ||
| + | De las ecuaciones de movimiento se deducen dos integrales primeras o constantes de movimiento: | ||
| + | |||
| + | ===Cantidad de movimiento del sistema=== | ||
| + | Sumando las dos ecuaciones | ||
| + | |||
| + | <center><math>0=m_1\ddot{x}_1+m_2\ddot{x}_2=\frac{\mathrm{d}\ }{\mathrm{d}t}(m_1\dot{x}_1+m_2\dot{x}_2)\qquad\Rightarrow\qquad m_1\dot{x}_1+m_2\dot{x}_2=\mathrm{cte}.</math></center> | ||
| + | |||
| + | con las condiciones iniciales de este problema | ||
| + | |||
| + | <center><math>m_1\dot{x}_1+m_2\dot{x}_2=m_1v_0</math></center> | ||
| + | |||
| + | Esta ecuación puede ser integrada de nuevo | ||
| + | |||
| + | <center><math>m_1x_1+m_2x_2=m_1v_0 t + m_2\ell_0</math></center> | ||
| + | |||
| + | De la conservación de la cantidad de movimiento se halla la velocidad y posición del CM | ||
| + | |||
| + | <center><math>\dot{x}_G=\frac{m_1\dot{x}_1+m_2\dot{x}_2}{m_1+m_2}= \frac{m_1}{m_1+m_2}v_0</math></center> | ||
| + | | ||
| + | <center><math>x_G=\frac{m_1x_1+m_2x_2}{m_1+m_2}= \frac{m_1}{m_1+m_2}v_0t+\frac{m_2\ell_0}{m_1+m_2}</math></center> | ||
| + | |||
| + | Vemos que el CM se mueve uniformemente, aunque su velocidad no es <math>v_0</math> sino una cantidad inferior. | ||
| + | |||
| + | ===Energía mecánica=== | ||
| + | Este sistema es conservativo, siendo su energía potencial | ||
| + | |||
| + | <center><math>U=\frac{1}{2}k(x_2-x_1-\ell_0)^2</math></center> | ||
| + | |||
| + | Por tanto se conserva su energía mecánica | ||
| + | |||
| + | <center><math>E = \frac{1}{2}(m_1\dot{x}_1^2+m_2\dot{x}_2^2)+\frac{1}{2}k(x_2-x_1-\ell_0)^2= \frac{1}{2}mv_0^2</math></center> | ||
==Ecuaciones horarias== | ==Ecuaciones horarias== | ||
| + | Para resolver el sistema de ecuaciones de movimiento | ||
| + | |||
| + | <center><math>\begin{array}{rcl} | ||
| + | m_1 \ddot{x}_1 & = & k(x_2-x_1-\ell_0) \\ | ||
| + | m_2 \ddot{x}_2 & = & -k(x_2-x_1-\ell_0) | ||
| + | \end{array}</math></center> | ||
| + | |||
| + | realizamos un cambio de variables. En lugar de las posiciones respectivas tomaremos la posición del CM | ||
| + | |||
| + | <center><math>x_G=\frac{m_1x_1+m_2x_2}{m_1+m_2}</math></center> | ||
| + | |||
| + | y la elongación del resorte | ||
| + | |||
| + | <center><math>x = x_2-x_1-\ell_0\,</math></center> | ||
| + | |||
| + | Una vez que determinemos estas dos cantidades como función del tiempo, podemos hallar la posición de cada masa invirtiendo estas relaciones | ||
| + | |||
| + | <center><math>x_1= x_G-\frac{m_2}{m_1+m_2}(x+\ell_0)\qquad\qquad x_2=x_G+\frac{m_1}{m_1+m_2}(x+\ell_0)</math></center> | ||
| + | |||
| + | La posición del CM como función del tiempo ya la hemos determinado a partir de la conservación de la cantidad de movimiento | ||
| + | |||
| + | <center><math>x_G=\frac{m_1}{m_1+m_2}v_0t+\frac{m_2\ell_0}{m_1+m_2}</math></center> | ||
| + | |||
| + | Nos queda hallar la ecuación para la elongación y resolverla. Las ecuaciones de movimiento las podemos escribir en la forma | ||
| + | |||
| + | <center><math>\begin{array}{rcl} | ||
| + | \ddot{x}_1 & = & \dfrac{k}{m_1}x \\ | ||
| + | \ddot{x}_2 & = & -\dfrac{k}{m_2}x | ||
| + | \end{array}</math></center> | ||
| + | |||
| + | Si restamos la primera de la segunda obtenemos la segunda derivada de la elongación | ||
| + | |||
| + | <center><math>\ddot{x}=\ddot{x}_2-\ddot{x}_1=-k\left(\frac{1}{m_1}+\frac{1}{m_2})x = -\omega^2 x</math></center> | ||
| + | |||
| + | que es la ecuación del oscilador armónico con la frecuencia al cuadrado | ||
| + | |||
| + | <center><math>\omega^2 = \frac{k}{m_1}+\frac{k}{m_2}</math></center> | ||
| + | |||
| + | La solución de esta ecuación diferencial es de la forma | ||
| + | |||
| + | <center><math>x=c_1 \cos(\omega t)+c_2\,\mathrm{sen}(\omega t)</math></center> | ||
| + | |||
| + | con los coeficientes que salen de las condiciones iniciales. En este caso tenemos | ||
| + | |||
| + | <center><math>x(t=0)=x_{20}-x_{10}-\ell_0=0\qquad\qquad \dot{x}(t=0)=\dot{x}_{20}-\dot{x}_{10}=-v_0</math></center> | ||
| + | |||
| + | Llevamos esto a la expresión de <math>x(t)</math> | ||
| + | |||
| + | <center><math>0=x(t=0)=c_1 \cos(\omega\cdot 0)+c_2\,\mathrm{sen}(\omega\cdot 0)=c_1\dtot 1 + c_2\dot 0 = c_1\qquad\Rightarrow\qquad c_1=0</math></center> | ||
| + | |||
| + | y de <math>\dot{x}(t)</math> | ||
| + | |||
| + | <center><math>-v_0=\dot{x}_(t=0)=-c_1\omega\,\mathrm{sen}(\omega\cdot 0) + c_2\omega\,\cos(\omega\cdot 0)=c_2\omega\qquad\Rightarrow\qquad c_2=-\frac{v_0}{\omega}</math></center> | ||
| + | |||
| + | Por tanto la elongación como función del tiempo es de la forma | ||
| + | |||
| + | <center><math>x(t)=-\frac{v_0}{\omega}\mathrm{sen}(\omega t)</math></center> | ||
| + | |||
| + | A partir de aquí obtenemos la posición de cada masa como función del tiempo | ||
| + | |||
| + | <center><math>\begin{array} | ||
| + | x_1(t)&=&\dfrac{m_1}{m_1+m_2}v_0t+\dfrac{m_2v_0}{(m_1+m2)\omega}\mathrm{sen}(\omega t)\\ | ||
| + | x_2(t) & = & \dfrac{m_1}{m_1+m_2}v_0t+\ell_0-\dfrac{m_1v_0}{(m_1+m2)\omega}\mathrm{sen}(\omega t) | ||
| + | \end{array}</math></center> | ||
| + | |||
| + | En las gráficas podemos ver el resultado para el caso de que la masa 1 sea igual a la 2, el que la 1 sea más masiva (y por tanto apenas se ve afectada por el resorte) o que sea muy ligera (en cuyo caso rebota y retrocede periódicamente). | ||
| + | |||
| + | |||
[[Categoría:Problemas de dinámica vectorial (CMR)]] | [[Categoría:Problemas de dinámica vectorial (CMR)]] | ||
Revisión de 17:46 12 dic 2017
Contenido |
1 Enunciado
Dos masas m1 y m2 se mueven a lo largo del eje OX unidas por un resorte de constante k y longitud natura 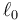 . Inicialmente las dos masas se encuentran en reposo en x10 = 0 y
. Inicialmente las dos masas se encuentran en reposo en x10 = 0 y 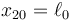 . Entonces se le comunica a la masa m1 una velocidad v0 en el sentido positivo del eje.
. Entonces se le comunica a la masa m1 una velocidad v0 en el sentido positivo del eje.
- Determine dos constantes de movimiento.
- Calcule la posición de cada una de las masas como función del tiempo. Sugerencia: realice el cambio de variables
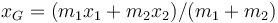 ,
,  .
.
2 Ecuaciones de movimiento
Las dos masas describen un movimiento rectilíneo, por lo que podemos emplear cantidades escalares, en lugar de vectores.
En ese caso, la segunda ley de Newton aplicada a cada partícula nos da

La fuerza que actúa sobre cada partícula es la debida al resorte (aparte estarían el peso y la normal, pero se cancelan mutuamente, por lo que no influyen). Esta fuerza está gobernada por la ley de Hooke

donde el signo es tal que si el muelle está estirado tiende a reunir las dos masas.
Por tanto, tenemos el sistema de ecuaciones diferenciales
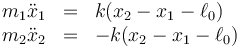
con las condiciones iniciales, en este caso

3 Constantes de movimiento
De las ecuaciones de movimiento se deducen dos integrales primeras o constantes de movimiento:
3.1 Cantidad de movimiento del sistema
Sumando las dos ecuaciones
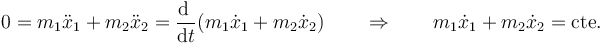
con las condiciones iniciales de este problema
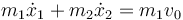
Esta ecuación puede ser integrada de nuevo
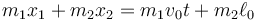
De la conservación de la cantidad de movimiento se halla la velocidad y posición del CM
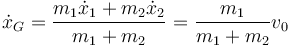
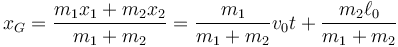
Vemos que el CM se mueve uniformemente, aunque su velocidad no es v0 sino una cantidad inferior.
3.2 Energía mecánica
Este sistema es conservativo, siendo su energía potencial
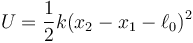
Por tanto se conserva su energía mecánica
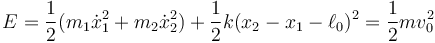
4 Ecuaciones horarias
Para resolver el sistema de ecuaciones de movimiento
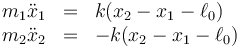
realizamos un cambio de variables. En lugar de las posiciones respectivas tomaremos la posición del CM
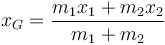
y la elongación del resorte
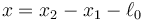
Una vez que determinemos estas dos cantidades como función del tiempo, podemos hallar la posición de cada masa invirtiendo estas relaciones

La posición del CM como función del tiempo ya la hemos determinado a partir de la conservación de la cantidad de movimiento
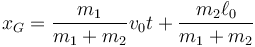
Nos queda hallar la ecuación para la elongación y resolverla. Las ecuaciones de movimiento las podemos escribir en la forma
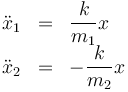
Si restamos la primera de la segunda obtenemos la segunda derivada de la elongación
que es la ecuación del oscilador armónico con la frecuencia al cuadrado
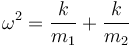
La solución de esta ecuación diferencial es de la forma

con los coeficientes que salen de las condiciones iniciales. En este caso tenemos

Llevamos esto a la expresión de x(t)
y de 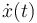
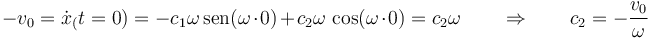
Por tanto la elongación como función del tiempo es de la forma
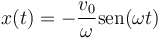
A partir de aquí obtenemos la posición de cada masa como función del tiempo
En las gráficas podemos ver el resultado para el caso de que la masa 1 sea igual a la 2, el que la 1 sea más masiva (y por tanto apenas se ve afectada por el resorte) o que sea muy ligera (en cuyo caso rebota y retrocede periódicamente).





