Problemas de dinámica vectorial (CMR2)
De Laplace
(→Dos masas unidas por un oscilador armónico) |
|||
| Línea 20: | Línea 20: | ||
# Demuestre que el centro de masas de las dos partículas describe un movimiento rectilíneo y uniforme. | # Demuestre que el centro de masas de las dos partículas describe un movimiento rectilíneo y uniforme. | ||
# Considerando la posición de cada partícula respecto al CM, determine la posición de cada una de ellas como función del tiempo. | # Considerando la posición de cada partícula respecto al CM, determine la posición de cada una de ellas como función del tiempo. | ||
| + | |||
| + | ==[[Movimiento a partir de una fuerza conocida]]== | ||
| + | Una partícula material de masa <math>m</math> parte del origen de coordenadas con velocidad <math>\vec{v}_0=v_0\vec{\jmath}</math>, encontrándose sometida en todo momento a la fuerza dependiente de la posición | ||
| + | |||
| + | <center><math>\vec{F}(x,y,z)=Az\vec{\imath}-By\vec{\jmath}+C\vec{k}</math></center> | ||
| + | |||
| + | siendo <math>\vec{r}=x\vec{\imath}+y\vec{\jmath}+z\vec{k}</math> la posición instantánea de la partícula, y <math>A</math>, <math>B</math> y <math>C</math> constantes positivas conocidas. | ||
| + | |||
| + | Calcule la posición, velocidad y aceleración instantáneas de la partícula para todo instante de tiempo, <math>t</math>. | ||
Revisión de 11:44 1 dic 2017
Contenido |
1 Oscilador armónico tridimensional
Una partícula se mueve en tres dimensiones de forma tal que verifica la ecuación del oscilador armónico
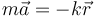
con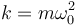 
y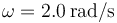 
. Su posición inicial es 
.
- Para el caso
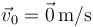. ¿Qué tipo de movimiento describe la partícula?
- Para el caso
, ¿cómo es la trayectoria? ¿Qué tipo de movimiento describe la partícula?
- Suponga ahora que
, ¿cómo es ahora la trayectoria de la partícula?
- Demuestre que en todos los casos la cantidad calculada en coordenadas polares
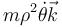es constante.
2 Dos masas unidas por un muelle
Dos masas m1 y m2 se mueven a lo largo del eje OX unidas por un resorte de constante k y longitud natura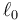 
. Inicialmente las dos masas se encuentran en reposo en x10 = 0 y 
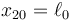. Entonces se le comunica a la masa m1 una velocidad v0 en el sentido positivo del eje.
- Determine dos constantes de movimiento.
- Calcule la posición de cada una de las masas como función del tiempo. Sugerencia: realice el cambio de variables xG = (m1x1 + m2x2) / (m1 + m2),
.
3 Dos masas unidas por un oscilador armónico
Suponga que en el problema “Oscilador armónico tridimensional” en lugar de una sola partícula tenemos dos, de masas m1 y m2, unidas por un resorte de constante k y longitud natural nula. Inicialmente la masa 1 se halla en reposo en el origen de coordenadas y la masa 2 se encuentra en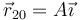 
moviéndose con velocidad 
.
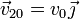- Demuestre que el centro de masas de las dos partículas describe un movimiento rectilíneo y uniforme.
- Considerando la posición de cada partícula respecto al CM, determine la posición de cada una de ellas como función del tiempo.
4 Movimiento a partir de una fuerza conocida
Una partícula material de masa m parte del origen de coordenadas con velocidad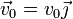 
, encontrándose sometida en todo momento a la fuerza dependiente de la posición
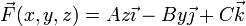
siendo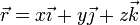 
la posición instantánea de la partícula, y A, B y C constantes positivas conocidas.
Calcule la posición, velocidad y aceleración instantáneas de la partícula para todo instante de tiempo, t.
