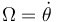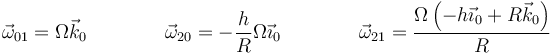Disco en varilla horizontal (CMR)
De Laplace
| Línea 9: | Línea 9: | ||
# Halle las aceleraciones angulares <math>\vec{\alpha}_{01}</math>, <math>\vec{\alpha}_{20}</math> y <math>\vec{\alpha}_{21}</math>. | # Halle las aceleraciones angulares <math>\vec{\alpha}_{01}</math>, <math>\vec{\alpha}_{20}</math> y <math>\vec{\alpha}_{21}</math>. | ||
# Calcule las aceleraciones en los movimientos {21} y {20} de los puntos C, G y D del apartado (3). | # Calcule las aceleraciones en los movimientos {21} y {20} de los puntos C, G y D del apartado (3). | ||
| + | |||
| + | ==Velocidades angulares== | ||
| + | En este problema tenemos tres sistemas de referencias, los dos sólidos y el sistema intermedio. Puesto que el punto A es fijo en los tres, podemos emplearlo como origen de coordenadas común. | ||
| + | |||
| + | El sistema 1 es el fijo, con ejes <math>OX_1</math> y <math>OY_1</math> horizontales y <math>OZ_1</math> vertical. | ||
| + | |||
| + | El sistema 0 tienes su eje <math>OX_0</math> siempre alineado con la varilla, siendo <math>OZ_0</math> vertical y coincidente con <math>OZ_1</math>. En el movimiento {01} este sistema gira en torno a <math>OZ_1=OZ_0</math> por lo que las bases respectivas cumplen | ||
| + | |||
| + | <center><math>\begin{array}{rcl}\vec{\imath}_0&=&\cos(\theta)\vec{\imath}_1+\mathrm{sen}(\theta)\vec{\jmath}_1\\ | ||
| + | \vec{\imath}_0&=&-\mathrm{sen}(\theta)\vec{\imath}_1+\cos(\theta)\vec{\jmath}_1\\ | ||
| + | \vec{k}_0&=&\vec{k}_1\end{array}</math></center> | ||
| + | |||
| + | La velocidad angular del movimiento {01} es una rotación en torno a su eje común | ||
| + | |||
| + | <center><math>\vec{\omega}_{01}=\dot{\theta}\vec{k}_1=\dot{\theta}\vec{k}_0</math></center> | ||
| + | |||
| + | El sistema 2 es uno ligado al disco y cuyo eje <math>OX_2</math> coincide con el <math>OX_2</math>. El disco gira alrededor de este eje. Por tanto, la relación entre las correspondientes bases es | ||
| + | |||
| + | <center><math>\begin{array}{rcl}\vec{\imath}_2&=&\vec{\imath}_0\\ | ||
| + | \vec{\jmath}_2&=&\cos(\psi)\vec{\jmath}_0+\mathrm{sen}(\psi)\vec{k}_0\\ | ||
| + | \vec{k}_2&=&-\mathrm{sen}(\psi)\vec{\jmath}_0+\cos\vec{k}_0\\ | ||
| + | \end{array}</math></center> | ||
| + | |||
| + | siendo la velocidad angular | ||
| + | |||
| + | <center><math>\vec{\omega}_{20}=\dot{\psi}\vec{\imath}_0=\dot{\psi}\vec{\imath}_2</math></center> | ||
| + | |||
| + | Aquí ψ es el ángulo que va girando el disco sobre su eje. No es una variable independiente de θ ya que debe cumplirse la condición de rodadura sin deslizamiento. | ||
| + | |||
| + | La velocidad angular del movimiento {21} es la composición de las otras dos | ||
| + | |||
| + | <center><math>\vec{\omega}_{21}=\vec{\omega}_{20}+\vec{\omega}_{01}=\dot{\psi}\vec{\imath}_0+\dot{\theta}\vec{k}_0</math></center> | ||
| + | |||
| + | Obtenemos la relación entre las dos componentes imponiendo la condición de que la velocidad en el punto de contacto C es nula en el movimiento {21} | ||
| + | |||
| + | <center><math>\vec{0}=\vec{v}^C_{21}=\overbrace{\vec{v}^A_{21}}^{=\vec{0}}+\vec{\omega}_{21}\times \overrightarrow{AC}</math></center> | ||
| + | |||
| + | Desarrollando el producto vectorial | ||
| + | |||
| + | <center><math>\vec{0}=\left(\dot{\psi}\vec{\imath}_0+\dot{\theta}\vec{k}_0\right)\times\left(h\vec{\imath}_0-R\vec{k}_0\right)=\left(R\dot{\psi}+h\dot{\theta}\right)\vec{\jmath}_0</math></center> | ||
| + | |||
| + | por lo que debe ser | ||
| + | |||
| + | <center><math>\dot{\psi}=-\frac{h}{R}\dot{\theta}\qquad\Rightarrow\qquad \psi=-\frac{h}{R}\theta</math></center> | ||
| + | |||
| + | y por tanto, si llamamos <math>\Omega=\dot{\theta}</math> | ||
| + | |||
| + | <center><math>\vec{\omega}_{01}=\Omega\vec{k}_0\qquad\qquad \vec{\omega}_{20}=-\frac{h}{R}\Omega\vec{\imath}_0\qquad\qquad\vec{\omega}_{21}=\frac{\Omega\left(-h\vec{\imath}_0+R\vec{k}_0\right)}{R}</math></center> | ||
| + | |||
[[Categoría:Problemas de cinemática del movimiento relativo (CMR)]] | [[Categoría:Problemas de cinemática del movimiento relativo (CMR)]] | ||
Revisión de 17:25 10 nov 2017
1 Enunciado
Un disco de radio R (“sólido 2”) se encuentra ensartado mediante un rodamiento sin fricción en un eje horizontal de longitud h (“sólido 0”). Este eje está montado sobre un soporte vertical fijo de altura R. El disco rueda sin deslizar sobre la superficie horizontal z = 0 (“sólido 1”). Consideramos tres sistemas de referencia. Uno fijo en el suelo, uno ligado al disco, y uno intermedio en el que el eje OX0 es a lo largo de la barra horizontal y OZ0 = OZ1 en todo momento. Sea (t) el ángulo que el eje OX0 forma con el OX1. En un instante dado 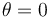 ,
, 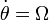 ,
, 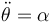 .
.
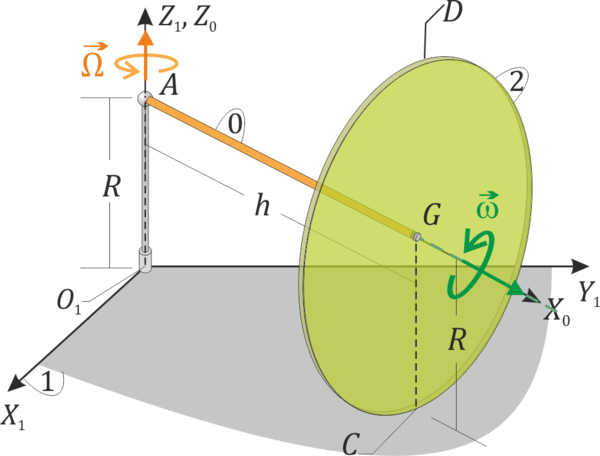
Para ese instante:
- Determine los vectores
 ,
,  y
y  .
.
- Halle la posición de los ejes instantáneos de rotación en los movimientos {01}, {20} y {21}.
- Calcule las velocidades en el movimiento {21} y el {20} del punto C de contacto del disco con el suelo; del G, centro del disco, y de D, el punto más alto del disco.
- Halle las aceleraciones angulares
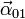 ,
, 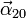 y
y 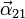 .
.
- Calcule las aceleraciones en los movimientos {21} y {20} de los puntos C, G y D del apartado (3).
2 Velocidades angulares
En este problema tenemos tres sistemas de referencias, los dos sólidos y el sistema intermedio. Puesto que el punto A es fijo en los tres, podemos emplearlo como origen de coordenadas común.
El sistema 1 es el fijo, con ejes OX1 y OY1 horizontales y OZ1 vertical.
El sistema 0 tienes su eje OX0 siempre alineado con la varilla, siendo OZ0 vertical y coincidente con OZ1. En el movimiento {01} este sistema gira en torno a OZ1 = OZ0 por lo que las bases respectivas cumplen
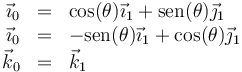
La velocidad angular del movimiento {01} es una rotación en torno a su eje común
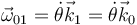
El sistema 2 es uno ligado al disco y cuyo eje OX2 coincide con el OX2. El disco gira alrededor de este eje. Por tanto, la relación entre las correspondientes bases es
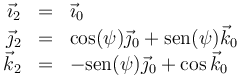
siendo la velocidad angular
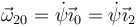
Aquí ψ es el ángulo que va girando el disco sobre su eje. No es una variable independiente de θ ya que debe cumplirse la condición de rodadura sin deslizamiento.
La velocidad angular del movimiento {21} es la composición de las otras dos
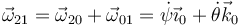
Obtenemos la relación entre las dos componentes imponiendo la condición de que la velocidad en el punto de contacto C es nula en el movimiento {21}
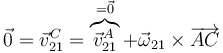
Desarrollando el producto vectorial
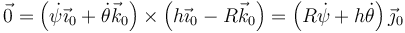
por lo que debe ser

y por tanto, si llamamos