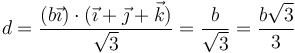Entrar Página Discusión Historial Go to the site toolbox

Test del primer parcial 2017-2018 (GIE)

De Laplace

(Diferencias entre revisiones)
 
(11 ediciones intermedias no se muestran.)
Línea 7: Línea 7:
;Solución:
;Solución:
La respuesta correcta es la '''<span style="color:red;">C<span>'''.
La respuesta correcta es la '''<span style="color:red;">C<span>'''.
 +
 +
La relación entre los momentos respecto a dos puntos diferentes es
 +
 +
<center><math>\vec{M}_A=\vec{M}_O+\vec{v}\times\overrightarrow{OA}</math></center>
 +
 +
Si son iguales
 +
 +
<center><math>\vec{M}_A=\vec{M}_O \qquad\Rightarrow\qquad\vec{v}\times\overrightarrow{OA}=\vec{0}</math></center>
 +
 +
y por tanto <math>\overrightarrow{OA}</math> es paralelo a <math>\vec{v}</math>
==Velocidad dependiente de x==
==Velocidad dependiente de x==
Línea 24: Línea 34:
La respuesta correcta es la '''<span style="color:red;">B<span>'''.
La respuesta correcta es la '''<span style="color:red;">B<span>'''.
 +
Por homogeneidad dimensional
 +
 +
<center><math>\frac{\mathrm{m}}{\mathrm{s}}=[A]\sqrt{\mathrm{m}^2}\qquad\Rightarrow\qquad [A]=\frac{1}{\mathrm{s}}</math></center>
===Pregunta 2===
===Pregunta 2===
¿Cuánto vale la aceleración de la partícula como función de x?
¿Cuánto vale la aceleración de la partícula como función de x?
Línea 31: Línea 44:
:* '''D''' <math>a=-Ax/\sqrt{b^2-x^2}</math>.
:* '''D''' <math>a=-Ax/\sqrt{b^2-x^2}</math>.
;Solución:
;Solución:
-
La respuesta correcta es la '''<span style="color:red;">D<span>'''.
+
La respuesta correcta es la '''<span style="color:red;">A<span>'''.
 +
 
 +
Se deriva respecto al tiempo aplicando la regla de la cadena
 +
 
 +
<center><math>a=\frac{\mathrm{d}v}{\mathrm{d}t}=\frac{\mathrm{d}v}{\mathrm{d}x}\,\overbrace{\frac{\mathrm{d}x}{\mathrm{d}t}}^{=v}=\frac{-Ax}{\sqrt{b^2-x^2}}A\sqrt{b^2-x^2}=-A^2x</math></center>
 +
 
 +
Equivalentemente se puede hallar como
 +
 
 +
<center><math>a=\frac{\mathrm{d}\ }{\mathrm{d}x}\left(\frac{1}{2}v^2\right)=\frac{\mathrm{d}\ }{\mathrm{d}x}\left(\frac{A^2(b^2-x^2)}{2}\right)=-A^2x</math></center>
===Pregunta 3===
===Pregunta 3===
Línea 42: Línea 63:
La respuesta correcta es la '''<span style="color:red;">C<span>'''.
La respuesta correcta es la '''<span style="color:red;">C<span>'''.
 +
De acuerdo con la pregunta anterior, la partícula cumple la ecuación del oscilador armonico
 +
 +
<center><math>a=-\omega^2 x\qquad\qquad\mbox{con}\qquad\omega = A\,</math></center>
 +
 +
y la solución es de la forma
 +
 +
<center><math>x = x_0\cos(A t)+\frac{v_{x0}}{A}\mathrm{sen}(A t)</math></center>
 +
 +
En este caso
 +
 +
<center><math>x_0=0\qquad\qquad v_0=A\sqrt{b^2-0^2}=Ab</math></center>
 +
 +
y queda
 +
 +
<center><math>x=b\,\mathrm{sen}(At)</math></center>
 +
 +
También puede hacerse sustituyendo las diferentes opciones en la ecuación para la velocidad, o integrando
 +
 +
<center><math>\frac{\mathrm{d}x}{\mathrm{d}t}=A\sqrt{b^2-x^2}\qquad\Rightarrow\qquad \int_0^x\frac{\mathrm{d}x}{\sqrt{b^2-x^2}}=A\int_0^t\mathrm{d}t</math></center>
==Triedro de Frenet==
==Triedro de Frenet==
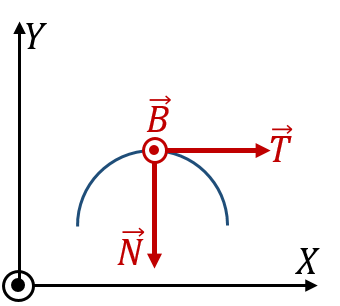
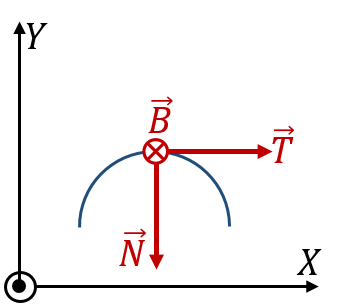
¿Cuál de las siguientes figuras representa correctamente la orientación de los vectores del triedro de Frenet (&#x2299;: hacia afuera del papel; &otimes; hacia adentro del papel)?
¿Cuál de las siguientes figuras representa correctamente la orientación de los vectores del triedro de Frenet (&#x2299;: hacia afuera del papel; &otimes; hacia adentro del papel)?
Línea 60: Línea 100:
|}
|}
 +
;Solución:
 +
La respuesta correcta es la '''<span style="color:red;">D<span>'''.
 +
 +
El vector normal <math>\vec{N}</math> está contenido en el plano del movimiento y dirigido hacia el interior de la curva, lo cual nos deja con las opciones B y D.
 +
 +
El vector binormal cumple la regla de la mano derecha respecto a <math>\vec{T}</math> y <math>\vec{N}</math>
 +
 +
<center><math>\vec{B}=\vec{T}\times\vec{N}</math></center>
 +
 +
por lo que el binormal debe ir hacia adentro y la respuesta es la D.
 +
 +
==Rapidez con incertidumbre==
 +
Se miden las componentes de una velocidad, con sus respectivas incertidumbres y resulta la cantidad <math>\vec{v}=(3.0(1)\vec{\imath}-4.0(1)\vec{\jmath}-8.0(1)\vec{k})  \mathrm{m}/\mathrm{s}</math>. ¿Cuánto vale la rapidez del movimiento?
 +
:* '''A''' 9.43(16)m/s
 +
:* '''B''' 89(3)m/s.
 +
:* '''C''' 89.0(1)m/s.
 +
:* '''D''' 9.43398(1)m/s.
 +
;Solución:
 +
La respuesta correcta es la '''<span style="color:red;">A<span>'''.
 +
 +
Podemos estimar la medida y su incertidumbre tomando los valores mínimo y máximo para cada componente. Así queda
 +
 +
<center><math>|\vec{v}|_\mathrm{min}=\sqrt{2.9^2+3.9^2+7.9^2}=9.27524\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
 +
 +
y
 +
 +
<center><math>|\vec{v}|_\mathrm{max}=\sqrt{3.1^2+4.1^2+8.1^2}=9.59323\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
 +
 +
La medida sería la media de estas dos
 +
 +
<center><math>|\vec{v}|=\frac{|\vec{v}|_\mathrm{min}+|\vec{v}|_\mathrm{max}}{2}=9.43423\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
 +
 +
y su incertidumbre la mitad de la diferencia
 +
 +
<center><math>E_v=\frac{|\vec{v}|_\mathrm{max}-|\vec{v}|_\mathrm{min}}{2}=0.158995\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
 +
 +
Redondeando queda
 +
 +
<center><math>|\vec{v}|=9.43(16)\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
 +
 +
También se puede llegar por eliminación, ya que no puede ser ni la B ni la C, y la D tiene un número excesivo de cifras significativas.
 +
 +
 +
==Velocidad media de dos tramos==
 +
Una partícula en movimiento rectilíneo recorre la primera mitad de la distancia con velocidad <math>v_1</math> y la segunda mitad con <math>v_2</math>, siempre en el mismo sentido. La velocidad media del trayecto es&hellip;
 +
:* '''A''' <math>v_m=(v_1+v_2)/2\,</math>.
 +
:* '''B''' <math>v_m=2v_1v_2/(v_1+v_2)\,</math>.
 +
:* '''C''' <math>v_m=\sqrt{(v_1^2+v_2^2)/2}</math>.
 +
:* '''D''' <math>v_m=\sqrt{v_1v_2}</math>.
 +
;Solución:
 +
La respuesta correcta es la '''<span style="color:red;">B<span>'''.
 +
 +
Los desplazamientos en cada mitad valen
 +
 +
<center><math>\Delta x_1=\Delta x_2=\frac{\Delta x}{2}</math></center>
 +
 +
Los intervalos empleados en recorrer cada mitad son
 +
 +
<center><math>\Delta t_1=\frac{\Delta x_1}{v_1}=\frac{\Delta x}{2v_1}\qquad\qquad \Delta t_2=\frac{\Delta x_2}{v_2}=\frac{\Delta x}{2v_2}</math></center>
 +
 +
y el total
 +
 +
<center><math>\Delta t = \Delta t_1+\Delta t_2=\frac{\Delta x}{2v_1}+\frac{\Delta x}{2v_2}=\frac{\Delta x(v_1+v_2)}{2v_1v_2}</math></center>
 +
 +
lo que da la velocidad media
 +
 +
<center><math>v_m=\frac{\Delta x}{\Delta t}=\frac{2v_1v_2}{v_1+v_2}</math></center>
 +
 +
==Distancia dentro de un cubo==
 +
Sea un cubo de arista <math>b</math> siendo O uno de sus vértices. ¿Cuánto mide la distancia de O al plano definido por sus tres vértices contiguos?
 +
:* '''A''' <math>b\sqrt{2}/2</math>.
 +
:* '''B''' <math>b\sqrt{3}/2</math>.
 +
:* '''C''' <math>b\sqrt{3}/3</math>.
 +
:* '''D''' <math>b/3</math>.
 +
;Solución:
 +
La respuesta correcta es la '''<span style="color:red;">C<span>'''.
 +
 +
La distancia de un punto O a un plano que pasa por A se calcula como
 +
 +
<center><math>d=\frac{\overrightarrow{OA}\cdot\vec{B}}{|\vec{B}|}</math></center>
 +
 +
siendo <math>\vec{B}</math> un vector perpendicular al plano. En este caso, <math>\vec{B}</math> va en la dirección de la diagonal del cubo
 +
 +
<center><math>\vec{B}=\vec{\imath}+\vec{\jmath}+\vec{k}\qquad\qquad |\vec{B}|=\sqrt{3}</math></center>
 +
 +
y <math>\overrightarrow{OA}</math> es el vector de O a un punto del plano, por ejemplo,
 +
 +
<center><math>\overrightarrow{OA}=b\vec{\imath}</math></center>
 +
 +
lo que da
 +
 +
<center><math>d = \frac{(b\vec{\imath})\cdot(\vec{\imath}+\vec{\jmath}+\vec{k})}{\sqrt{3}}=\frac{b}{\sqrt{3}}=\frac{b\sqrt{3}}{3}</math></center>
[[Categoría:Preguntas de test de Física I (GIE)]]
[[Categoría:Preguntas de test de Física I (GIE)]]

última version al 08:51 25 oct 2017

Contenido

1 Momentos de un vector

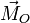Un vector \vec{v} está aplicado en el punto P. Se conocen sus momentos \vec{M}_O respecto a un punto O y 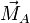\vec{M}_A respecto a un punto A. Si 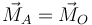\vec{M}_A=\vec{M}_O se cumple que…

  • A \overrightarrow{OP} es paralelo a \vec{v}.
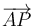  • B \overrightarrow{AP} es paralelo a \vec{v}.
  • C \overrightarrow{OA} es paralelo a \vec{v}.
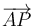  • D \overrightarrow{OP} es paralelo a \overrightarrow{AP}.
Solución

La respuesta correcta es la C.

La relación entre los momentos respecto a dos puntos diferentes es

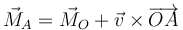
\vec{M}_A=\vec{M}_O+\vec{v}\times\overrightarrow{OA}

Si son iguales

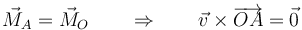
\vec{M}_A=\vec{M}_O \qquad\Rightarrow\qquad\vec{v}\times\overrightarrow{OA}=\vec{0}

y por tanto \overrightarrow{OA} es paralelo a \vec{v}

2 Velocidad dependiente de x

Una partícula se mueve a lo largo de la recta OX cumpliéndose en todo momento

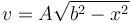
v=A\sqrt{b^2-x^2}

con A y b dos constantes positivas. La partícula se halla inicialmente en x = 0.

2.1 Pregunta 1

¿En qué unidades se mide A en el sistema internacional?

  • A m/s.
  • B 1/s.
  • C m²/s.
  • D m³/s
Solución

La respuesta correcta es la B.

Por homogeneidad dimensional

\frac{\mathrm{m}}{\mathrm{s}}=[A]\sqrt{\mathrm{m}^2}\qquad\Rightarrow\qquad [A]=\frac{1}{\mathrm{s}}

2.2 Pregunta 2

¿Cuánto vale la aceleración de la partícula como función de x?

  • A a=-A^2x\,.
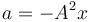  • B No hay información suficiente para determinarla.
  • C a=0\,
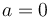
  • D 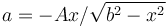a=-Ax/\sqrt{b^2-x^2}.
Solución

La respuesta correcta es la A.

Se deriva respecto al tiempo aplicando la regla de la cadena

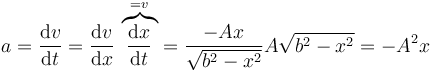
a=\frac{\mathrm{d}v}{\mathrm{d}t}=\frac{\mathrm{d}v}{\mathrm{d}x}\,\overbrace{\frac{\mathrm{d}x}{\mathrm{d}t}}^{=v}=\frac{-Ax}{\sqrt{b^2-x^2}}A\sqrt{b^2-x^2}=-A^2x

Equivalentemente se puede hallar como

a=\frac{\mathrm{d}\ }{\mathrm{d}x}\left(\frac{1}{2}v^2\right)=\frac{\mathrm{d}\ }{\mathrm{d}x}\left(\frac{A^2(b^2-x^2)}{2}\right)=-A^2x

2.3 Pregunta 3

¿Cuál es la posición de la partícula como función del tiempo, para todo t?

  • A x=0\,.
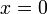  • B No hay información suficiente para determinarla.
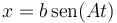
  • C x=b\,\mathrm{sen}(At)
  • D 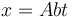x=A b t\,.
Solución

La respuesta correcta es la C.

De acuerdo con la pregunta anterior, la partícula cumple la ecuación del oscilador armonico

a=-\omega^2 x\qquad\qquad\mbox{con}\qquad\omega = A\,

y la solución es de la forma

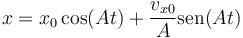
x = x_0\cos(A t)+\frac{v_{x0}}{A}\mathrm{sen}(A t)

En este caso

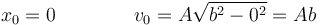
x_0=0\qquad\qquad v_0=A\sqrt{b^2-0^2}=Ab

y queda

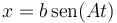
x=b\,\mathrm{sen}(At)

También puede hacerse sustituyendo las diferentes opciones en la ecuación para la velocidad, o integrando

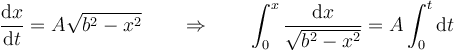
\frac{\mathrm{d}x}{\mathrm{d}t}=A\sqrt{b^2-x^2}\qquad\Rightarrow\qquad \int_0^x\frac{\mathrm{d}x}{\sqrt{b^2-x^2}}=A\int_0^t\mathrm{d}t

3 Triedro de Frenet

¿Cuál de las siguientes figuras representa correctamente la orientación de los vectores del triedro de Frenet (⊙: hacia afuera del papel; ⊗ hacia adentro del papel)?

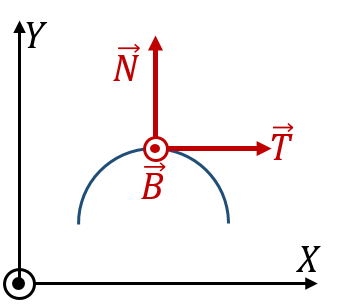
Archivo:caso-frenet-01.png Archivo:caso-frenet-02.png
A B
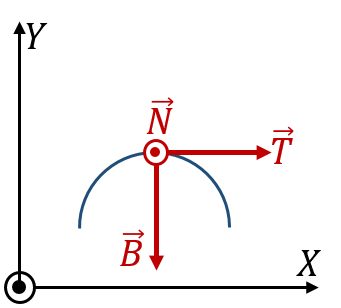
Archivo:caso-frenet-03.png Archivo:caso-frenet-04.png
C D
Solución

La respuesta correcta es la D.

El vector normal \vec{N} está contenido en el plano del movimiento y dirigido hacia el interior de la curva, lo cual nos deja con las opciones B y D.

El vector binormal cumple la regla de la mano derecha respecto a \vec{T} y \vec{N}

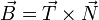
\vec{B}=\vec{T}\times\vec{N}

por lo que el binormal debe ir hacia adentro y la respuesta es la D.

4 Rapidez con incertidumbre

Se miden las componentes de una velocidad, con sus respectivas incertidumbres y resulta la cantidad \vec{v}=(3.0(1)\vec{\imath}-4.0(1)\vec{\jmath}-8.0(1)\vec{k}) \mathrm{m}/\mathrm{s}. ¿Cuánto vale la rapidez del movimiento?

  • A 9.43(16)m/s
  • B 89(3)m/s.
  • C 89.0(1)m/s.
  • D 9.43398(1)m/s.
Solución

La respuesta correcta es la A.

Podemos estimar la medida y su incertidumbre tomando los valores mínimo y máximo para cada componente. Así queda

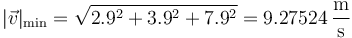
|\vec{v}|_\mathrm{min}=\sqrt{2.9^2+3.9^2+7.9^2}=9.27524\,\frac{\mathrm{m}}{\mathrm{s}}

y

|\vec{v}|_\mathrm{max}=\sqrt{3.1^2+4.1^2+8.1^2}=9.59323\,\frac{\mathrm{m}}{\mathrm{s}}

La medida sería la media de estas dos

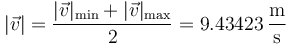
|\vec{v}|=\frac{|\vec{v}|_\mathrm{min}+|\vec{v}|_\mathrm{max}}{2}=9.43423\,\frac{\mathrm{m}}{\mathrm{s}}

y su incertidumbre la mitad de la diferencia

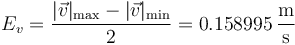
E_v=\frac{|\vec{v}|_\mathrm{max}-|\vec{v}|_\mathrm{min}}{2}=0.158995\,\frac{\mathrm{m}}{\mathrm{s}}

Redondeando queda

|\vec{v}|=9.43(16)\,\frac{\mathrm{m}}{\mathrm{s}}

También se puede llegar por eliminación, ya que no puede ser ni la B ni la C, y la D tiene un número excesivo de cifras significativas.


5 Velocidad media de dos tramos

Una partícula en movimiento rectilíneo recorre la primera mitad de la distancia con velocidad v1 y la segunda mitad con v2, siempre en el mismo sentido. La velocidad media del trayecto es…

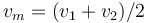  • A v_m=(v_1+v_2)/2\,.
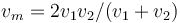  • B v_m=2v_1v_2/(v_1+v_2)\,.
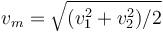  • C v_m=\sqrt{(v_1^2+v_2^2)/2}.
  • D v_m=\sqrt{v_1v_2}.
Solución

La respuesta correcta es la B.

Los desplazamientos en cada mitad valen

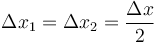
\Delta x_1=\Delta x_2=\frac{\Delta x}{2}

Los intervalos empleados en recorrer cada mitad son

\Delta t_1=\frac{\Delta x_1}{v_1}=\frac{\Delta x}{2v_1}\qquad\qquad \Delta t_2=\frac{\Delta x_2}{v_2}=\frac{\Delta x}{2v_2}

y el total

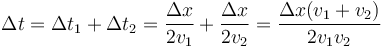
\Delta t = \Delta t_1+\Delta t_2=\frac{\Delta x}{2v_1}+\frac{\Delta x}{2v_2}=\frac{\Delta x(v_1+v_2)}{2v_1v_2}

lo que da la velocidad media

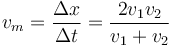
v_m=\frac{\Delta x}{\Delta t}=\frac{2v_1v_2}{v_1+v_2}

6 Distancia dentro de un cubo

Sea un cubo de arista b siendo O uno de sus vértices. ¿Cuánto mide la distancia de O al plano definido por sus tres vértices contiguos?

  • A 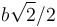b\sqrt{2}/2.
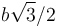  • B b\sqrt{3}/2.
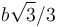  • C b\sqrt{3}/3.
  • D b / 3.
Solución

La respuesta correcta es la C.

La distancia de un punto O a un plano que pasa por A se calcula como

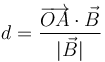
d=\frac{\overrightarrow{OA}\cdot\vec{B}}{|\vec{B}|}

siendo \vec{B} un vector perpendicular al plano. En este caso, \vec{B} va en la dirección de la diagonal del cubo

\vec{B}=\vec{\imath}+\vec{\jmath}+\vec{k}\qquad\qquad |\vec{B}|=\sqrt{3}

y \overrightarrow{OA} es el vector de O a un punto del plano, por ejemplo,

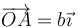
\overrightarrow{OA}=b\vec{\imath}

lo que da

d = \frac{(b\vec{\imath})\cdot(\vec{\imath}+\vec{\jmath}+\vec{k})}{\sqrt{3}}=\frac{b}{\sqrt{3}}=\frac{b\sqrt{3}}{3}

Obtenido de "http://tesla.us.es/wiki/index.php/Test_del_primer_parcial_2017-2018_(GIE)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 08:51, 25 oct 2017. - Esta página ha sido visitada 2.379 veces. - Aviso legal - Acerca de Laplace