Problemas de cinemática de la partícula (CMR)
De Laplace
(Página creada con '==Cálculo de velocidad media== Una partícula describe un movimiento rectilíneo tal que su velocidad instantánea cumple la ley <center>…') |
|||
| Línea 26: | Línea 26: | ||
# Halle el triedro de Frenet en <math>t=1\,\mathrm{s}</math>. | # Halle el triedro de Frenet en <math>t=1\,\mathrm{s}</math>. | ||
# Calcule el radio de curvatura en <math>t=1\,\mathrm{s}</math> así como el centro de curvatura en ese instante. | # Calcule el radio de curvatura en <math>t=1\,\mathrm{s}</math> así como el centro de curvatura en ese instante. | ||
| + | |||
| + | ==[[Estudio de un movimiento tridimensional]]== | ||
| + | Una partícula se mueve según las ecuaciones horarias | ||
| + | |||
| + | <center><math>\vec{r}(t)=B\cos^2(\Omega t)\vec{\imath}+2B\,\mathrm{sen}^2(\Omega t)\vec{\jmath}+2B\cos^2(\Omega t)\vec{k}</math></center> | ||
| + | |||
| + | # ¿Qué trayectoria sigue la partícula? | ||
| + | # Determine la ley horaria <math>s(t)</math>. Suponga que <math>s(0)=0</math>. | ||
| + | # ¿Qué tipo de movimiento describe la partícula? | ||
| + | |||
| + | ==[[Movimiento circular en 3D]]== | ||
| + | Una partícula se mueve según las ecuaciones horarias | ||
| + | |||
| + | <center><math>\vec{r}(t)=4A\cos(\Omega t)\vec{\imath}+ 5A\,\mathrm{sen}(\Omega t)\vec{\jmath}+3A\cos(\Omega t)\vec{k}</math></center> | ||
| + | |||
| + | con A y Ω constantes. | ||
| + | |||
| + | # ¿Qué trayectoria sigue la partícula? | ||
| + | # ¿Qué desplazamiento realiza y qué distancia recorre la partícula entre t=0 y t = π/Ω? | ||
| + | # Justifique que este movimiento es circular y uniforme | ||
| + | # Determine la posición del centro del movimiento circular | ||
| + | # Calcule la velocidad angular de este movimiento circular | ||
| + | |||
| + | ==[[Ejemplo de movimiento helicoidal (GIE)|Ejemplo de movimiento helicoidal ]]== | ||
| + | El movimiento de un pájaro en una corriente térmica es aproximadamente helicoidal, compuesto de un movimiento ascensional y uno de giro alrededor del eje de subida, de forma que la velocidad en cada punto de la trayectoria puede escribirse como | ||
| + | |||
| + | <center><math>\vec{v}=\vec{v}_0+\vec{\omega}_0\times\vec{r}</math></center> | ||
| + | |||
| + | siendo | ||
| + | |||
| + | <center><math>\vec{v}_0 = v_0\vec{k}\qquad \vec{\omega}_0=\omega_0 \vec{k}</math></center> | ||
| + | |||
| + | dos vectores constantes. Si la posición inicial es <math>\vec{r}_0=A\vec{\imath}</math> | ||
| + | |||
| + | # Determine las ecuaciones horarias del movimiento. ¿Qué trayectoria describe? | ||
| + | # Halle los vectores tangente, normal y binormal para un instante arbitrario. | ||
| + | # Determine la aceleración tangencial, la normal y el radio de curvatura en cualquier instante. | ||
| + | # Calcule la distancia recorrida por la partícula en un intervalo de tiempo T=2π⁄ω_0 | ||
| + | |||
| + | |||
| + | |||
[[Categoría:Problemas de cinemática de la partícula (CMR)]] | [[Categoría:Problemas de cinemática de la partícula (CMR)]] | ||
Revisión de 20:03 12 oct 2017
Contenido |
1 Cálculo de velocidad media
Una partícula describe un movimiento rectilíneo tal que su velocidad instantánea cumple la ley
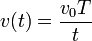
¿Cuánto vale la velocidad media entre 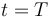 y
y 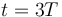 ?
?
2 Tiro parabólico sobre una pendiente
Se desea alcanzar un blanco que se encuentra sobre un plano inclinado un ángulo β, estando el blanco a una distancia D del punto de disparo.
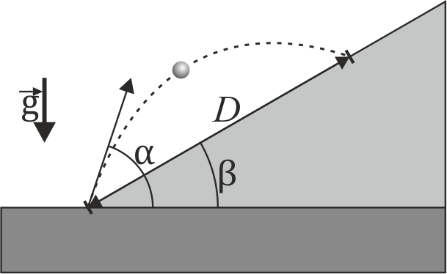
- ¿Cuál es la rapidez mínima que debe tener el proyectil para llegar al blanco? ¿Con qué ángulo sobre la horizontal debe dispararse en ese caso?
- Suponga que el plano tiene una pendiente del 75% y el proyectil se lanza con el ángulo que da el alcance máximo para llegar a D = 100 m. Para este caso, halle:
- La rapidez que tiene en el momento del impacto.
- La aceleración tangencial y normal (escalares) en el momento de impacto.
Tómese 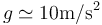 .
.
3 Análisis de ecuación horaria
Una partícula se mueve por el espacio de forma que su velocidad, en las unidades fundamentales del SI, viene dada por la ecuación horaria
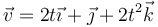
Inicialmente la partícula se encuentra en 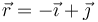 .
.
- Calcule la posición en función del tiempo y el desplazamiento entre
 y
y 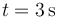 . ¿Cuánto vale la velocidad media en dicho intervalo?
. ¿Cuánto vale la velocidad media en dicho intervalo?
- Halle la rapidez en cada instante, así como la distancia que recorre la partícula en el mismo intervalo de tiempo. ¿Cuánto vale la rapidez media en este intervalo?
- Halle las componentes intrínsecas de la aceleración en
 , como escalares y como vectores.
, como escalares y como vectores.
- Halle el triedro de Frenet en
 .
.
- Calcule el radio de curvatura en
 así como el centro de curvatura en ese instante.
así como el centro de curvatura en ese instante.
4 Estudio de un movimiento tridimensional
Una partícula se mueve según las ecuaciones horarias
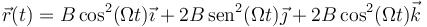
- ¿Qué trayectoria sigue la partícula?
- Determine la ley horaria s(t). Suponga que s(0) = 0.
- ¿Qué tipo de movimiento describe la partícula?
5 Movimiento circular en 3D
Una partícula se mueve según las ecuaciones horarias
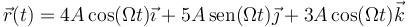
con A y Ω constantes.
- ¿Qué trayectoria sigue la partícula?
- ¿Qué desplazamiento realiza y qué distancia recorre la partícula entre t=0 y t = π/Ω?
- Justifique que este movimiento es circular y uniforme
- Determine la posición del centro del movimiento circular
- Calcule la velocidad angular de este movimiento circular
6 Ejemplo de movimiento helicoidal
El movimiento de un pájaro en una corriente térmica es aproximadamente helicoidal, compuesto de un movimiento ascensional y uno de giro alrededor del eje de subida, de forma que la velocidad en cada punto de la trayectoria puede escribirse como
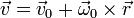
siendo

dos vectores constantes. Si la posición inicial es 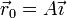
- Determine las ecuaciones horarias del movimiento. ¿Qué trayectoria describe?
- Halle los vectores tangente, normal y binormal para un instante arbitrario.
- Determine la aceleración tangencial, la normal y el radio de curvatura en cualquier instante.
- Calcule la distancia recorrida por la partícula en un intervalo de tiempo T=2π⁄ω_0





