Entrar Página Discusión Historial Go to the site toolbox

Movimientos en 2D y 3D (G.I.C.)

De Laplace

(Diferencias entre revisiones)
(→Caso 2)
Línea 4: Línea 4:
curvas que definen las trayectorias en los movimientos descritos por las leyes
curvas que definen las trayectorias en los movimientos descritos por las leyes
horarias siguientes
horarias siguientes
 +
#<math>\vec{r}(t) = R\cos(\omega t)\,\vec{\imath} + A\,\mathrm{sen}\,(\omega t)\,\vec{\jmath} </math>, con <math>R</math> y <math>\omega</math> constantes.
#<math>\vec{r}(t) = A\cos\alpha\,\mathrm{sen}\,(\omega t)\,\vec{\imath} + A\,\mathrm{sen}\,\alpha\,\mathrm{sen}\,(\omega t)\,\vec{\jmath} </math>, con <math>A</math>, <math>\omega</math> y <math>\alpha</math> constantes.
#<math>\vec{r}(t) = A\cos\alpha\,\mathrm{sen}\,(\omega t)\,\vec{\imath} + A\,\mathrm{sen}\,\alpha\,\mathrm{sen}\,(\omega t)\,\vec{\jmath} </math>, con <math>A</math>, <math>\omega</math> y <math>\alpha</math> constantes.
#<math>\vec{r}(t) = At\,\vec{\imath} + Bt^2\,\vec{\jmath} </math>, con <math>A</math> y <math>B</math> constantes.
#<math>\vec{r}(t) = At\,\vec{\imath} + Bt^2\,\vec{\jmath} </math>, con <math>A</math> y <math>B</math> constantes.
 +
#<math>\vec{r}(t) = \dfrac{A(T^2-t^2)}{T^2+t^2}\,\vec{\imath} + \dfrac{2ATt}{T^2+t^2}\,\vec{\jmath} </math>, con <math>A</math> y <math>T</math> constantes.
= Solución =
= Solución =
== Caso 1 ==
== Caso 1 ==
 +
[[File:GIERM_P01_cir.png|right|300px]]
 +
La velocidad es
 +
<center>
 +
<math>
 +
\vec{v} = \dot{\vec{r}} = -R\omega\,\mathrm{sen}\,(\omega t)\,\vec{\imath} +
 +
R\omega\cos(\omega t)\,\vec{\jmath}
 +
</math>
 +
</center>
 +
La rapidez es
 +
<center>
 +
<math>
 +
|\vec{v}| = R\omega
 +
</math>
 +
</center>
 +
El desplazamiento elemental
 +
<center>
 +
<math>
 +
\mathrm{d}\vec{r} = \vec{v}\mathrm{d}t =
 +
(-R\omega\,\mathrm{sen}\,(\omega t)\,\vec{\imath} +
 +
R\omega\cos(\omega t)\,\vec{\jmath})\,\mathrm{d}t
 +
</math>
 +
</center>
 +
La aceleración es
 +
<center>
 +
<math>
 +
\vec{a} = \dot{\vec{v}} = -R\omega^2\cos(\omega t)\,\vec{\imath} -
 +
R\omega^2\,\mathrm{sen}\,(\omega t)\,\vec{\jmath}
 +
 +
</math>
 +
</center>
 +
Buscamos la ecuación de la trayectoria en forma implícita. Escribiendo en forma de ecuaciones paramétricas tenemos
 +
<center>
 +
<math>
 +
\vec{r} = \left\{
 +
\begin{array}{l}
 +
x = R\cos(\omega t) \\
 +
y = R\,\mathrm{sen}\,(\omega t)
 +
\end{array}
 +
\right.
 +
</math>
 +
</center>
 +
Vemos que
 +
<center>
 +
<math>
 +
x^2 + y^2 = R^2
 +
</math>
 +
</center>
 +
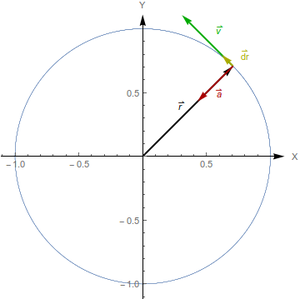
Es una circunferencia de radio <math>R</math> centrada en el origen.
 +
 +
 +
== Caso 2 ==
[[File:GIERM_P01_1.png|right]]
[[File:GIERM_P01_1.png|right]]
El vector de posición puede escribirse así
El vector de posición puede escribirse así
Línea 62: Línea 115:
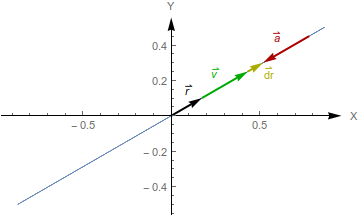
Es una línea recta que pasa por el origen y tiene pendiente <math>\tan\alpha</math>. Esto ya puede verse al escribir el vector de posición como una función escalar del tiempo por un vector constante
Es una línea recta que pasa por el origen y tiene pendiente <math>\tan\alpha</math>. Esto ya puede verse al escribir el vector de posición como una función escalar del tiempo por un vector constante
-
== Caso 2 ==
+
== Caso 3 ==
[[File:GIERM_P01_2.png|right]]
[[File:GIERM_P01_2.png|right]]
La velocidad es
La velocidad es
Línea 107: Línea 160:
</center>
</center>
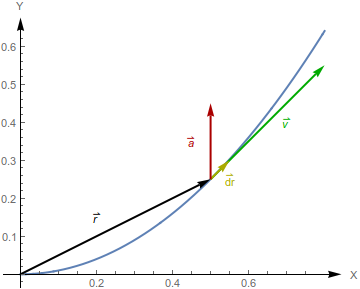
Es una parábola con la concavidad hacia arriba
Es una parábola con la concavidad hacia arriba
 +
 +
== Caso 4 ==
 +
[[File:GIERM_P01_4.png|right|300px]]
 +
La velocidad es
 +
<center>
 +
<math>
 +
\vec{v} = \dot{\vec{r}} =
 +
\dfrac{2AT}{T^2+t^2}\,(-2Tt\,\vec{\imath} + (T^2-t^2)\,\vec{\jmath})
 +
</math>
 +
</center>
 +
La rapidez es
 +
<center>
 +
<math>
 +
|\vec{v}| = \dfrac{2AT}{T^2+t^2}
 +
</math>
 +
</center>
 +
El desplazamiento elemental
 +
<center>
 +
<math>
 +
\mathrm{d}\vec{r} = \vec{v}\mathrm{d}t =
 +
\dfrac{2AT}{T^2+t^2}\,(-2Tt\,\vec{\imath} + (T^2-t^2)\,\vec{\jmath})\,\mathrm{d}t
 +
</math>
 +
</center>
 +
La aceleración es
 +
<center>
 +
<math>
 +
\vec{a} =
 +
\dfrac{4AT}{(T^2+t^2)^3}\,(T(3t^2-T^2)\,\vec{\imath} +
 +
t(t^2-3T^2)\,\vec{\jmath})
 +
</math>
 +
</center>
 +
Buscamos la ecuación de la trayectoria en forma implícita. Escribiendo en forma de ecuaciones paramétricas tenemos
 +
<center>
 +
<math>
 +
\vec{r} = \left\{
 +
\begin{array}{l}
 +
x =  \dfrac{A(T^2-t^2)}{T^2+t^2}\\ \\
 +
y = \dfrac{2ATt}{T^2+t^2}
 +
\end{array}
 +
\right.
 +
</math>
 +
</center>
 +
Tomando el cuadrado de los dos vemos que
 +
<center>
 +
<math>
 +
\begin{array}{l}
 +
x^2 =  A^2\dfrac{(T^4+t^4-2T^2t^2)}{(T^2+t^2)^2}\\ \\
 +
y^2 = A^2\dfrac{4T^2t^2}{(T^2+t^2)^2}
 +
\end{array}
 +
</math>
 +
</center>
 +
Sumando los dos
 +
<center>
 +
<math>
 +
x^2 + y^2 = A^2\dfrac{T^4+t^4+2T^2t^2}{(T^2+t^2)^2}=
 +
A^2\dfrac{(T^2+t^2)^2}{(T^2+t^2)^2}=A^2
 +
</math>
 +
</center>
 +
 +
Es una circunferencia de radio <math>R</math> centrada en el origen.

Revisión de 12:50 29 sep 2017

Contenido

1 Enunciado

1.1 Movimientos en 2D y 3D

Calcula la velocidad, rapidez, aceleración, desplazamiento elemental y las curvas que definen las trayectorias en los movimientos descritos por las leyes horarias siguientes

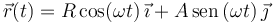  1. \vec{r}(t) = R\cos(\omega t)\,\vec{\imath} + A\,\mathrm{sen}\,(\omega t)\,\vec{\jmath} , con R y ω constantes.
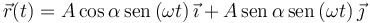  2. \vec{r}(t) = A\cos\alpha\,\mathrm{sen}\,(\omega t)\,\vec{\imath} + A\,\mathrm{sen}\,\alpha\,\mathrm{sen}\,(\omega t)\,\vec{\jmath} , con A, ω y α constantes.
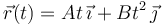  3. \vec{r}(t) = At\,\vec{\imath} + Bt^2\,\vec{\jmath} , con A y B constantes.
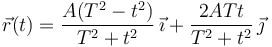  4. \vec{r}(t) = \dfrac{A(T^2-t^2)}{T^2+t^2}\,\vec{\imath} + \dfrac{2ATt}{T^2+t^2}\,\vec{\jmath} , con A y T constantes.

2 Solución

2.1 Caso 1

La velocidad es

\vec{v} = \dot{\vec{r}} = -R\omega\,\mathrm{sen}\,(\omega t)\,\vec{\imath} + R\omega\cos(\omega t)\,\vec{\jmath}

La rapidez es

|\vec{v}| = R\omega

El desplazamiento elemental

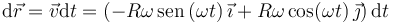
\mathrm{d}\vec{r} = \vec{v}\mathrm{d}t = (-R\omega\,\mathrm{sen}\,(\omega t)\,\vec{\imath} + R\omega\cos(\omega t)\,\vec{\jmath})\,\mathrm{d}t

La aceleración es

\vec{a} = \dot{\vec{v}} = -R\omega^2\cos(\omega t)\,\vec{\imath} - R\omega^2\,\mathrm{sen}\,(\omega t)\,\vec{\jmath}

Buscamos la ecuación de la trayectoria en forma implícita. Escribiendo en forma de ecuaciones paramétricas tenemos

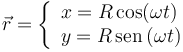
\vec{r} = \left\{ \begin{array}{l} x = R\cos(\omega t) \\ y = R\,\mathrm{sen}\,(\omega t) \end{array} \right.

Vemos que

x2 + y2 = R2

Es una circunferencia de radio R centrada en el origen.


2.2 Caso 2

El vector de posición puede escribirse así

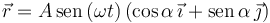
\vec{r} = A\,\mathrm{sen}\,(\omega t)\,(\cos\alpha\,\vec{\imath}+\mathrm{sen}\,\alpha\,\vec{\jmath})

Sólo el primer factor depende del tiempo. La velocidad es

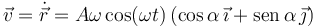
\vec{v} = \dot{\vec{r}} = A\omega\cos(\omega t)\,(\cos\alpha\,\vec{\imath} + \mathrm{sen}\,\alpha\,\vec{\jmath})

La rapidez es

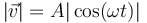
|\vec{v}| = A |\cos(\omega t)|

El desplazamiento elemental

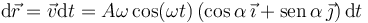
\mathrm{d}\vec{r} = \vec{v}\mathrm{d}t = A\omega\cos(\omega t)\,(\cos\alpha\,\vec{\imath} + \mathrm{sen}\,\alpha\,\vec{\jmath}) \,\mathrm{d}t

La aceleración es

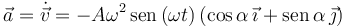
\vec{a} = \dot{\vec{v}} = -A\omega^2\,\mathrm{sen}\,(\omega t)\,(\cos\alpha\,\vec{\imath} + \mathrm{sen}\,\alpha\,\vec{\jmath})

Buscamos la ecuación de la trayectoria en forma implícita. Escribiendo en forma de ecuaciones paramétricas tenemos

\vec{r} = \left\{ \begin{array}{l} x = A\,\mathrm{sen}\,(\omega t)\cos\alpha\\ y = A\,\mathrm{sen}\,(\omega t)\,\mathrm{sen}\,\alpha \end{array} \right.

Vemos que

\dfrac{y}{x} = \tan\alpha \Longrightarrow y = x\,\tan\alpha

Es una línea recta que pasa por el origen y tiene pendiente tanα. Esto ya puede verse al escribir el vector de posición como una función escalar del tiempo por un vector constante

2.3 Caso 3

La velocidad es

\vec{v} = \dot{\vec{r}} = A\,\vec{\imath} + 2Bt\,\vec{\jmath}

La rapidez es

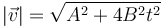
|\vec{v}| = \sqrt{A^2 + 4B^2t^2}

El desplazamiento elemental

\mathrm{d}\vec{r} = \vec{v}\mathrm{d}t = ( A\,\vec{\imath} + 2Bt\,\vec{\jmath})\,\mathrm{d}t

La aceleración es

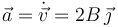
\vec{a} = \dot{\vec{v}} = 2B\,\vec{\jmath}

Buscamos la ecuación de la trayectoria en forma implícita. Escribiendo en forma de ecuaciones paramétricas tenemos

\vec{r} = \left\{ \begin{array}{l} x = At\\ y = B t^2 \end{array} \right.

Despejando t en la primera y sustituyendo en la segunda vemos que

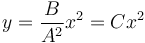
y = \dfrac{B}{A^2}x^2 = Cx^2

Es una parábola con la concavidad hacia arriba

2.4 Caso 4

La velocidad es

\vec{v} = \dot{\vec{r}} = \dfrac{2AT}{T^2+t^2}\,(-2Tt\,\vec{\imath} + (T^2-t^2)\,\vec{\jmath})

La rapidez es

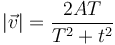
|\vec{v}| = \dfrac{2AT}{T^2+t^2}

El desplazamiento elemental

\mathrm{d}\vec{r} = \vec{v}\mathrm{d}t = \dfrac{2AT}{T^2+t^2}\,(-2Tt\,\vec{\imath} + (T^2-t^2)\,\vec{\jmath})\,\mathrm{d}t

La aceleración es

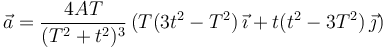
\vec{a} = \dfrac{4AT}{(T^2+t^2)^3}\,(T(3t^2-T^2)\,\vec{\imath} + t(t^2-3T^2)\,\vec{\jmath})

Buscamos la ecuación de la trayectoria en forma implícita. Escribiendo en forma de ecuaciones paramétricas tenemos

\vec{r} = \left\{ \begin{array}{l} x = \dfrac{A(T^2-t^2)}{T^2+t^2}\\ \\ y = \dfrac{2ATt}{T^2+t^2} \end{array} \right.

Tomando el cuadrado de los dos vemos que

\begin{array}{l} x^2 = A^2\dfrac{(T^4+t^4-2T^2t^2)}{(T^2+t^2)^2}\\ \\ y^2 = A^2\dfrac{4T^2t^2}{(T^2+t^2)^2} \end{array}

Sumando los dos

x^2 + y^2 = A^2\dfrac{T^4+t^4+2T^2t^2}{(T^2+t^2)^2}= A^2\dfrac{(T^2+t^2)^2}{(T^2+t^2)^2}=A^2

Es una circunferencia de radio R centrada en el origen.

Obtenido de "http://tesla.us.es/wiki/index.php/Movimientos_en_2D_y_3D_(G.I.C.)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace