Anilla ensartada en dos varillas rotatorias (GIE)
De Laplace
(Página creada con '==Enunciado== Una pequeña anilla se halla ensartada en las dos barras rotatorias de la figura. Las dos barras giran alrededor de puntos fijos O y A que distan una cantidad b. L…') |
|||
| (9 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| - | Una pequeña anilla se halla ensartada en las dos barras rotatorias de la figura. Las dos barras giran alrededor de puntos fijos O y A que distan una cantidad b. Las dos barras giran en sentido positivo, la de O con velocidad angular 2Ω y la de A con velocidad angular Ω. Inicialmente la barra de O se halla situada horizontalmente y la de A verticalmente. | + | Una pequeña anilla se halla ensartada en las dos barras rotatorias de la figura. Las dos barras giran alrededor de puntos fijos <math>O</math> y <math>A</math> que distan una cantidad <math>b</math>. Las dos barras giran en sentido positivo, la de O con velocidad angular 2Ω y la de A con velocidad angular Ω. Inicialmente la barra de O se halla situada horizontalmente y la de A verticalmente.<center> |
| - | + | [[Archivo:barras-anilla.png|300px]]</center> | |
| - | + | # Determine la posición, velocidad y aceleración de la anilla como función del tiempo. | |
| - | + | # Para el instante en que <math>\mathrm{tg}(\Omega t)=1/2</math> halle | |
| - | + | ## La posición, velocidad y aceleración de la anilla. | |
| - | El triedro de Frenet referido a la base canónica { | + | ## El triedro de Frenet referido a la base canónica <math>\left\{\vec{\imath},\vec{\jmath},\vec{k}\right\}</math> |
| - | + | ## Las componentes intrínsecas de la aceleración (escalares). | |
| - | + | ## El radio y el centro de curvatura. | |
| + | ==Posición, velocidad y aceleración== | ||
| + | ===Determinación de la posición=== | ||
| + | La posición en cada instante se halla conocida la distancia <math>|\overrightarrow{OP}|</math> como | ||
| + | |||
| + | <center><math>\vec{r}=|\overrightarrow{OP}|\left(\cos(2\Omega t)\vec{\imath}+\mathrm{sen}(2\Omega t)\right)</math></center> | ||
| + | |||
| + | La distancia <math>|\overrightarrow{OP}|</math> la calculamos resolviendo el triángulo OAP, del cual conocemos un lado y dos ángulos | ||
| + | |||
| + | <center><math>|\overrightarrow{OA}|=b\qquad\qquad \widehat{AOP}=2\Omega t\qquad\qquad \widehat{OAP}=\frac{\pi}{2}-\Omega t</math></center> | ||
| + | |||
| + | El tercer ángulo sale de que la suma de los tres es <math>\pi</math> | ||
| + | |||
| + | <center><math>\widehat{APO}=\pi-(2\Omega t)-\left(\frac{\pi}{2}-\Omega t\right)=\frac{\pi}{2}-\Omega t=\widehat{OAP}</math></center> | ||
| + | |||
| + | Al haber dos ángulos iguales el triángulo es isósceles y los dos lados son iguales | ||
| + | |||
| + | <center><math>|\overrightarrow{OP}|=|\overrightarrow{OA}|=b</math></center> | ||
| + | |||
| + | lo que nos da la posición en cada instante | ||
| + | |||
| + | <center><math>\vec{r}=b\left(\cos(2\Omega t)\vec{\imath}+\mathrm{sen}(2\Omega t)\right)</math></center> | ||
| + | |||
| + | Es decir, la anilla describe un movimiento circular uniforme alrededor del origen de coordenadas, con velocidad angular <math>2\Omega</math>. | ||
| + | ===Velocidad=== | ||
| + | Derivamos una vez | ||
| + | <center><math>\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=-2\Omega b\,\mathrm{sen}(2\Omega t)\vec{\imath}+2\Omega b\cos(2\Omega t)\vec{\jmath}</math></center> | ||
| + | |||
| + | La rapidez de este movmiento es constante |\vec{v}|=2\Omega b | ||
| + | ===Aceleración=== | ||
| + | Derivamos una segunda vez | ||
| + | |||
| + | <center><math>\vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=-4\Omega ^2b\,\cos(2\Omega t)\vec{\imath}-4\Omega^2 b\,\mathrm{sen}(2\Omega t)\vec{\jmath}</math></center> | ||
| + | |||
| + | Esta aceleración es puramente normal, como corresponde a un movimiento uniforme. | ||
| + | ==Valores en un instante concreto== | ||
| + | Cuando <math>\mathrm{tg}(\Omega t)=1/2</math> se cumple | ||
| + | |||
| + | <center><math>\cos(2\Omega t)=\frac{1-(1/2)^2}{1+(1/2)^2}=\frac{3}{5}\qquad\qquad \mathrm{sen}(2\Omega t)=\frac{2(1/2)}{1+(1/2)^2}=\frac{4}{5}</math></center> | ||
| + | |||
| + | y por tanto, aplicando reiteradamente que se trata de un movimiento circular uniforme | ||
| + | |||
| + | ;Posición: | ||
| + | |||
| + | <center><math>\vec{r}=\frac{3b}{5}\vec{\imath}+\frac{4b}{5}\vec{\jmath}</math></center> | ||
| + | |||
| + | ;Velocidad: | ||
| + | |||
| + | <center><math>\vec{v}=-\frac{8\Omega b}{5}\vec{\imath}+\frac{6\Omega b}{5}\vec{\jmath}</math></center> | ||
| + | |||
| + | ;Aceleración: | ||
| + | |||
| + | <center><math>\vec{a}=-\frac{12\Omega b}{5}\vec{\imath}-\frac{16\Omega b}{5}\vec{\jmath}</math></center> | ||
| + | |||
| + | ;Vector tangente: | ||
| + | |||
| + | <center><math>\vec{T}=\frac{\vec{v}}{|\vec{v}|}=-\frac{4}{5}\vec{\imath}+\frac{3}{5}\vec{\jmath}</math></center> | ||
| + | |||
| + | ;Vector normal: | ||
| + | |||
| + | <center><math>\vec{N}=\frac{\vec{a}}{|\vec{a}|}=-\frac{3}{5}\vec{\imath}-\frac{4}{5}\vec{\jmath}</math></center> | ||
| + | |||
| + | ;Vector binormal: | ||
| + | |||
| + | <center><math>\vec{B}=\vec{T}\times\vec{N}=\vec{k}</math></center> | ||
| + | |||
| + | ;Radio de curvatura: | ||
| + | |||
| + | <center><math>R=b\,</math></center> | ||
| + | |||
| + | ;Centro de curvatura: | ||
| + | |||
| + | <center><math>\overrightarrow{OC}=\overrightarrow{OO}=\vec{0}</math></center> | ||
última version al 18:09 20 sep 2017
Contenido[ocultar] |
1 Enunciado
Una pequeña anilla se halla ensartada en las dos barras rotatorias de la figura. Las dos barras giran alrededor de puntos fijos O y A que distan una cantidad b. Las dos barras giran en sentido positivo, la de O con velocidad angular 2Ω y la de A con velocidad angular Ω. Inicialmente la barra de O se halla situada horizontalmente y la de A verticalmente.
- Determine la posición, velocidad y aceleración de la anilla como función del tiempo.
- Para el instante en que tg(Ωt) = 1 / 2 halle
- La posición, velocidad y aceleración de la anilla.
- El triedro de Frenet referido a la base canónica
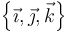
- Las componentes intrínsecas de la aceleración (escalares).
- El radio y el centro de curvatura.
2 Posición, velocidad y aceleración
2.1 Determinación de la posición
La posición en cada instante se halla conocida la distancia 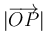 como
como
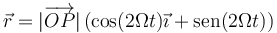
La distancia 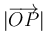 la calculamos resolviendo el triángulo OAP, del cual conocemos un lado y dos ángulos
la calculamos resolviendo el triángulo OAP, del cual conocemos un lado y dos ángulos

El tercer ángulo sale de que la suma de los tres es π

Al haber dos ángulos iguales el triángulo es isósceles y los dos lados son iguales

lo que nos da la posición en cada instante
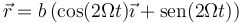
Es decir, la anilla describe un movimiento circular uniforme alrededor del origen de coordenadas, con velocidad angular 2Ω.
2.2 Velocidad
Derivamos una vez
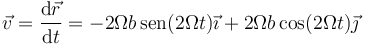
La rapidez de este movmiento es constante |\vec{v}|=2\Omega b
2.3 Aceleración
Derivamos una segunda vez

Esta aceleración es puramente normal, como corresponde a un movimiento uniforme.
3 Valores en un instante concreto
Cuando tg(Ωt) = 1 / 2 se cumple

y por tanto, aplicando reiteradamente que se trata de un movimiento circular uniforme
- Posición

- Velocidad
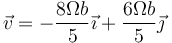
- Aceleración
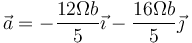
- Vector tangente

- Vector normal
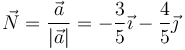
- Vector binormal
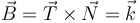
- Radio de curvatura

- Centro de curvatura






