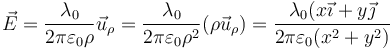Campo eléctrico de un segmento
De Laplace
| (5 ediciones intermedias no se muestran.) | |||
| Línea 25: | Línea 25: | ||
Llevando esto a la integral nos queda | Llevando esto a la integral nos queda | ||
| - | <center><math>\vec{E}=\frac{\lambda_0}{4\pi\varepsilon_0}\int_{-a}^a\frac{(x\vec{\imath}-z'\vec{k})\mathrm{d}z'}{(x^2+z'^2)^{3/2}}</math></center> | + | <center><math>\vec{E}=\frac{\lambda_0}{4\pi\varepsilon_0}\int_{-a}^a\frac{\left(x\vec{\imath}-z'\vec{k}\right)\mathrm{d}z'}{(x^2+z'^2)^{3/2}}</math></center> |
Esta integral vectorial se descompone en dos integrales escalares. De éstas, la segunda se anula | Esta integral vectorial se descompone en dos integrales escalares. De éstas, la segunda se anula | ||
| - | <center><math>\int_{-a}^a \frac{z'\,\mathrm{d}z'}{(x^2+z'^2)^{3/2}}</math></center> | + | <center><math>\int_{-a}^a \frac{z'\,\mathrm{d}z'}{(x^2+z'^2)^{3/2}}=0</math></center> |
por tratarse de una integral de una función impar sobre un intervalo simétrico. Esto nos deja con | por tratarse de una integral de una función impar sobre un intervalo simétrico. Esto nos deja con | ||
| Línea 35: | Línea 35: | ||
<center><math>\vec{E}=\frac{\lambda_0x\vec{\imath}}{4\pi\varepsilon_0}\int_{-a}^a\frac{\mathrm{d}z'}{(x^2+z'^2)^{3/2}}</math></center> | <center><math>\vec{E}=\frac{\lambda_0x\vec{\imath}}{4\pi\varepsilon_0}\int_{-a}^a\frac{\mathrm{d}z'}{(x^2+z'^2)^{3/2}}</math></center> | ||
| + | Esta integral se resuelve mediante el cambio de variable | ||
| + | |||
| + | <center><math>z'=x\,\mathrm{tg}(\alpha)\qquad\Rightarrow\qquad x^2+z'^2 = \frac{x^2}{\cos^2(\alpha)}\qquad\qquad \mathrm{d}z'=\frac{x\,\mathrm{d}\alpha}{\cos^2(\alpha)}</math></center> | ||
| + | |||
| + | Este ángulo posee una interpretación geométrica: es el ángulo de elevación respecto a la horizontal con el que se ve un punto del segmento desde la posición donde queremos hallar el campo. Con este cambio de variable la integral se transforma en | ||
| + | |||
| + | <center><math>\vec{E}=\frac{\lambda_0 x\vec{\imath}}{4\pi\varepsilon_0}\int_{-\alpha_0}^{\alpha_0}\frac{x\,\mathrm{d}\alpha}{\cos^2(\alpha)}\,\frac{\cos^3(\alpha)}{x^3}=\frac{\lambda_0\vec{\imath}}{4\pi\varepsilon_0 x}\int_{-\alpha_0}^{\alpha_0}\cos(\alpha)\mathrm{d}\alpha</math></center> | ||
| + | |||
| + | El límite de integración lo da el ángulo de elevación del extremo del segmento | ||
| + | |||
| + | <center><math>\mathrm{tg}(\alpha)_0=\frac{a}{x}\qquad\Rightarrow\qquad \mathrm{sen}(\alpha_0)=\frac{a}{\sqrt{a^2+x^2}}</math></center> | ||
| + | |||
| + | Con esto, la expresión para el campo eléctrico queda | ||
| + | |||
| + | <center><math>\vec{E}=\frac{\lambda_0 \mathrm{sen}(\alpha_0)\vec{\imath}}{2\pi\varepsilon_0 x}=\frac{\lambda_0 a\vec{\imath}}{2\pi\varepsilon_0 x\sqrt{x^2+a^2}}</math></center> | ||
==Hilo infinito== | ==Hilo infinito== | ||
| + | Podemos calcular el campo de un hilo infinito a partir del de un segmento considerando el límite en que la longitud de éste se hace infinita. En términos del ángulo de elevación <math>\alpha_0</math> equivale a hacer | ||
| + | |||
| + | <center><math>\alpha_0\to \frac{\pi}{2}\qquad\Rightarrow\qquad \vec{E}\to \frac{\lambda_0 \vec{\imath}}{2\pi\varepsilon_0 x}</math></center> | ||
| + | |||
| + | Esta expresión está particularizada para el caso de que el punto donde medimos el campo esté situado sobre el eje OX. La generalización a un punto arbitrio es inmediata. | ||
| + | |||
| + | Para un punto cualquiera, sustituimos x por la distancia al eje OZ (o, aun más en general, la línea donde se halla el hilo de carga). Empleando coordenadas cilíndricas, equivale sustituir <math>x</math> por <math>\rho=(x^2+y^2)^{1/2}</math>. | ||
| + | |||
| + | Además debemos dar la dirección del campo. En el caso del eje OX, <math>\vec{\imath}</math> es el unitario en el sentido de x creciente, esto es, el que se aleja en línea recta del eje OX. La generalización a cualquier punto consiste en sustituir <math>\vec{\imath}</math> por el unitario radial <math>\vec{u}_\rho</math>. | ||
| + | |||
| + | Por tanto, la expresión del campo creado por un hilo cargado uniformemente es, en cualquier punto del espacio, | ||
| + | |||
| + | <center><math>\vec{E}=\frac{\lambda_0}{2\pi\varepsilon_0\rho}\vec{u}_\rho</math></center> | ||
| + | |||
| + | Podemos expresar este resultado en la base cartesiana como | ||
| + | |||
| + | <center><math>\vec{E}=\frac{\lambda_0}{2\pi\varepsilon_0\rho}\vec{u}_\rho=\frac{\lambda_0}{2\pi\varepsilon_0\rho^2}(\rho\vec{u}_\rho)=\frac{\lambda_0(x\vec{\imath}+y\vec{\jmath}}{2\pi\varepsilon_0(x^2+y^2)}</math></center> | ||
[[Categoría:Problemas de electrostática en el vacío (GIE)]] | [[Categoría:Problemas de electrostática en el vacío (GIE)]] | ||
última version al 00:55 11 ene 2006
Contenido |
1 Enunciado
Calcule el campo eléctrico producido por un segmento rectilíneo cargado uniformemente con una densidad de carga λ0 en cualquier punto del plano perpendicular al segmento por su punto medio.
A partir del resultado anterior, halle el campo eléctrico creado por un hilo rectilíneo infinitamente largo cargado con una densidad homogénea λ0.
2 Segmento
El campo eléctrico creado por una distribución lineal de carga es
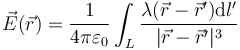
En nuestro caso, situamos el segmento cargado en el eje OZ y centrado en el origen de coordenadas, de forma que los puntos donde se encuentran las cargas cumplen
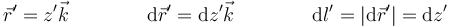
la variable z' irá de − a a + a.
Para los puntos donde medimos el campo nos dicen que se trata de un punto del plano central z = 0
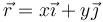
No obstante, dado que el sistema tiene simetría de revolución respecto al eje Z podemos considerar simplemente un punto del eje OX y luego generalizar. En este caso
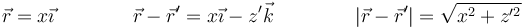
Llevando esto a la integral nos queda
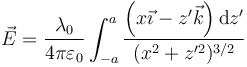
Esta integral vectorial se descompone en dos integrales escalares. De éstas, la segunda se anula
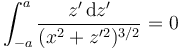
por tratarse de una integral de una función impar sobre un intervalo simétrico. Esto nos deja con
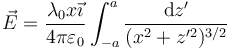
Esta integral se resuelve mediante el cambio de variable
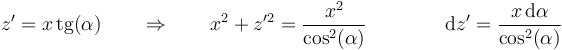
Este ángulo posee una interpretación geométrica: es el ángulo de elevación respecto a la horizontal con el que se ve un punto del segmento desde la posición donde queremos hallar el campo. Con este cambio de variable la integral se transforma en
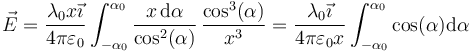
El límite de integración lo da el ángulo de elevación del extremo del segmento
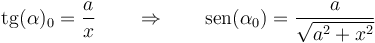
Con esto, la expresión para el campo eléctrico queda
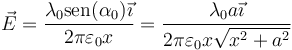
3 Hilo infinito
Podemos calcular el campo de un hilo infinito a partir del de un segmento considerando el límite en que la longitud de éste se hace infinita. En términos del ángulo de elevación α0 equivale a hacer

Esta expresión está particularizada para el caso de que el punto donde medimos el campo esté situado sobre el eje OX. La generalización a un punto arbitrio es inmediata.
Para un punto cualquiera, sustituimos x por la distancia al eje OZ (o, aun más en general, la línea donde se halla el hilo de carga). Empleando coordenadas cilíndricas, equivale sustituir x por ρ = (x2 + y2)1 / 2.
Además debemos dar la dirección del campo. En el caso del eje OX,  es el unitario en el sentido de x creciente, esto es, el que se aleja en línea recta del eje OX. La generalización a cualquier punto consiste en sustituir
es el unitario en el sentido de x creciente, esto es, el que se aleja en línea recta del eje OX. La generalización a cualquier punto consiste en sustituir  por el unitario radial
por el unitario radial 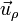 .
.
Por tanto, la expresión del campo creado por un hilo cargado uniformemente es, en cualquier punto del espacio,
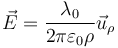
Podemos expresar este resultado en la base cartesiana como