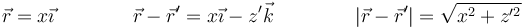Campo eléctrico de un segmento
De Laplace
(→Segmento) |
|||
| Línea 12: | Línea 12: | ||
<center><math>\vec{r}'=z'\vec{k}\qquad \qquad \mathrm{d}\vec{r}'=\mathrm{d}z'\vec{k}\qquad\qquad \mathrm{d}l'=|\mathrm{d}\vec{r}'|=\mathrm{d}z'</math></center> | <center><math>\vec{r}'=z'\vec{k}\qquad \qquad \mathrm{d}\vec{r}'=\mathrm{d}z'\vec{k}\qquad\qquad \mathrm{d}l'=|\mathrm{d}\vec{r}'|=\mathrm{d}z'</math></center> | ||
| + | |||
| + | la variable <math>z'</math> irá de <math>-a</math> a <math>+a</math>. | ||
| + | |||
| + | Para los puntos donde medimos el campo nos dicen que se trata de un punto del plano central <math>z=0</math> | ||
| + | <center><math> | ||
| + | \vec{r}=x\vec{\imath}+y\vec{\jmath}</math></center> | ||
| + | |||
| + | No obstante, dado que el sistema tiene simetría de revolución respecto al eje Z podemos considerar simplemente un punto del eje OX y luego generalizar. En este caso | ||
| + | |||
| + | <center><math>\vec{r}=x\vec{\imath}\qquad\qquad \vec{r}-\vec{r}'=x\vec{\imath}-z'\vec{k}\qquad\qquad \left|\vec{r}-\vec{r}'\right|=\sqrt{x^2+z'^2}</math></center> | ||
| + | |||
==Hilo infinito== | ==Hilo infinito== | ||
[[Categoría:Problemas de electrostática en el vacío (GIE)]] | [[Categoría:Problemas de electrostática en el vacío (GIE)]] | ||
Revisión de 20:25 28 mar 2017
Contenido |
1 Enunciado
Calcule el campo eléctrico producido por un segmento rectilíneo cargado uniformemente con una densidad de carga λ0 en cualquier punto del plano perpendicular al segmento por su punto medio.
A partir del resultado anterior, halle el campo eléctrico creado por un hilo rectilíneo infinitamente largo cargado con una densidad homogénea λ0.
2 Segmento
El campo eléctrico creado por una distribución lineal de carga es
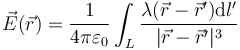
En nuestro caso, situamos el segmento cargado en el eje OZ y centrado en el origen de coordenadas, de forma que los puntos donde se encuentran las cargas cumplen
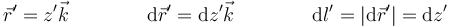
la variable z' irá de − a a + a.
Para los puntos donde medimos el campo nos dicen que se trata de un punto del plano central z = 0
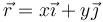
No obstante, dado que el sistema tiene simetría de revolución respecto al eje Z podemos considerar simplemente un punto del eje OX y luego generalizar. En este caso