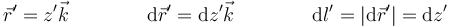Campo eléctrico de un segmento
De Laplace
(Diferencias entre revisiones)
| Línea 7: | Línea 7: | ||
El campo eléctrico creado por una distribución lineal de carga es | El campo eléctrico creado por una distribución lineal de carga es | ||
| - | <center><math>\vec{E}(\vec{r})=\frac{1}{4\pi\varepsilon_0}\int_L\frac{\lambda(\vec{r}-\vec{r}')\mathrm{d}l'}{|\vec{r}-\vec{r}'|^3}</math></center> | + | <center><math>\vec{E}(\vec{r})=\frac{1}{4\pi\varepsilon_0}\int_L\frac{\lambda(\vec{r}-\vec{r}')\mathrm{d}l'}{|\vec{r}-\vec{r}'|^3}</math></center> |
| + | |||
| + | En nuestro caso, situamos el segmento cargado en el eje OZ y centrado en el origen de coordenadas, de forma que los puntos donde se encuentran las cargas cumplen | ||
| + | |||
| + | <center><math>\vec{r}'=z'\vec{k}\qquad \qquad \mathrm{d}\vec{r}'=\mathrm{d}z'\vec{k}\qquad\qquad \mathrm{d}l'=|\mathrm{d}\vec{r}'|=\mathrm{d}z'</math></center> | ||
==Hilo infinito== | ==Hilo infinito== | ||
[[Categoría:Problemas de electrostática en el vacío (GIE)]] | [[Categoría:Problemas de electrostática en el vacío (GIE)]] | ||
Revisión de 20:22 28 mar 2017
Contenido |
1 Enunciado
Calcule el campo eléctrico producido por un segmento rectilíneo cargado uniformemente con una densidad de carga λ0 en cualquier punto del plano perpendicular al segmento por su punto medio.
A partir del resultado anterior, halle el campo eléctrico creado por un hilo rectilíneo infinitamente largo cargado con una densidad homogénea λ0.
2 Segmento
El campo eléctrico creado por una distribución lineal de carga es
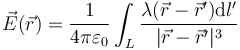
En nuestro caso, situamos el segmento cargado en el eje OZ y centrado en el origen de coordenadas, de forma que los puntos donde se encuentran las cargas cumplen