Oscilador no lineal
De Laplace
(Diferencias entre revisiones)
(→Enunciado) |
|||
| Línea 11: | Línea 11: | ||
==Solución== | ==Solución== | ||
===Energía mecánica=== | ===Energía mecánica=== | ||
| + | Esta fuerza, dependiente solo de la posición, es una fuerza conservativa, que deriva de una energía potencial | ||
===Movimiento periódico=== | ===Movimiento periódico=== | ||
===Puntos de equilibrio=== | ===Puntos de equilibrio=== | ||
===Pequeñas oscilaciones=== | ===Pequeñas oscilaciones=== | ||
[[Categoría:Problemas de movimiento oscilatorio]] | [[Categoría:Problemas de movimiento oscilatorio]] | ||
Revisión de 11:55 8 feb 2009
Contenido |
1 Enunciado
Una partícula está sometida exclusivamente a una fuerza, dependiente de la posición, dada por
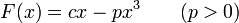
- Halle la expresión de la energía potencial y la energía mecánica para la partícula. Esboce las gráficas para los casos c < 0 y c > 0.
- Demuestre que el movimiento de la partícula siempre es acotado, y periódico.
- Localice las posiciones de equilibrio de la partícula (a) si c < 0 (b) si c > 0.
- Suponga que la partícula se suelta desde una posición muy próxima a las posiciones de equilibrio calculadas en el apartado anterior. ¿En qué caso describe oscilaciones? Halle el valor aproximado del periodo de oscilación para este movimiento.
2 Solución
2.1 Energía mecánica
Esta fuerza, dependiente solo de la posición, es una fuerza conservativa, que deriva de una energía potencial





