Ecuaciones de Lagrange (CMR)

De Laplace

(Diferencias entre revisiones)

última version al 15:08 22 ene 2017

Contenido

1 Introducción
2 Ecuaciones de Euler-Lagrange
3 Fuerzas conservativas

1 Introducción

Al introducir las coordenadas generalizadas llegamos a que el principio de D'Alembert puede escribirse en la forma

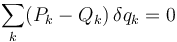
$\sum_k(P_k-Q_k)\,\delta q_k = 0$

En el caso particular importante de que todos los vínculos sean holónomos y podamos definir 3N-r coordenadas generalizadas intependientes, cada uno de los coeficientes debe anularse por separado y obtenemos el sistema de ecuaciones

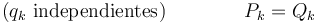
$(q_k\ \mbox{independientes})\qquad\qquad P_k=Q_k$

Aquí las cantidades $Q k$ son las fuerzas generalizadas

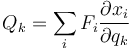
$Q_k = \sum_i F_i\frac{\partial x_i}{\partial q_k}$

a las que se le puede dar una interpretación relativamente simple: son las componentes (en un sentido amplio) de las fuerzas que pueden producir un cambio en la coordenada $q k$ . Si esta coordenada es cartesiana, $Q k$ representa una fuerza usual; si es un ángulo, representa el momento de una fuerza (que es el que produce un giro) y así sucesivamente.

Los términos $P k$ no tienen una interpretación inmediata. Se definen como

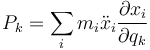
$P_k = \sum_i m_i\ddot{x}_i\frac{\partial x_i}{\partial q_k}$

y podemos decir que $- P k$ representa una fuerza de inercia generalizada, pero esta interpretación no aporta mucho, ya que esa fuerza de inercia requiere hallar la aceleración de las partículas, lo que es precisamente uno de los objetivos de la dinámica, por lo que no se pueden tratar como fuerzas aplicadas.

En lo que sigue deduciremos expresiones alternativas para $P k$ que proporcionan un método sistemático para la determinación de estas fuerzas de inercia generalizadas que no requiera conocer la solución del problema que queremos resolver.

2 Ecuaciones de Euler-Lagrange

2.1 Dos identidades utiles

Definimos un conjunto de coordenadas generalizadas $q k$ de manera que las coordenadas cartesianas de las diferentes partículas se escriben

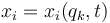
$x_i=x_i(q_k,t)\,$

A partir de las relaciones entre coordenadas hallamos la relación entre velocidades derivando

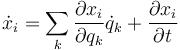
$\dot{x}_i=\sum_k\frac{\partial x_i}{\partial q_k}\dot{q}_k+\frac{\partial x_i}{\partial t}$

La velocidad 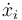$\dot{x}_i$ es una función de las coordenadas generalizadas, de las velocidades generalizadas y del tiempo. De la expresión anterior se deduce que

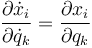
$\frac{\partial \dot{x}_i}{\partial \dot{q}_k}=\frac{\partial x_i}{\partial q_k}$

Por otro lado, si hallamos la derivada total respecto al tiempo de la derivada parcial

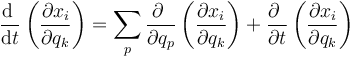
$\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial x_i}{\partial q_k}\right)=\sum_p\frac{\partial\ }{\partial q_p}\left(\frac{\partial x_i}{\partial q_k}\right)+\frac{\partial\ }{\partial t}\left(\frac{\partial x_i}{\partial q_k}\right)$

Por las propiedades de las derivadas parciales se puede invertir el orden de cada derivada cruzada

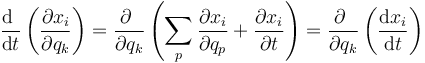
$\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial x_i}{\partial q_k}\right)=\frac{\partial \ }{\partial q_k}\left(\sum_p\frac{\partial x_i}{\partial q_p}+\frac{\partial x_i}{\partial t}\right)=\frac{\partial\ }{\partial q_k}\left(\frac{\mathrm{d}x_i}{\mathrm{d}t}\right)$

Es decir, resulta la identidad

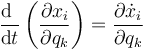
$\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial x_i}{\partial q_k}\right)=\frac{\partial\dot{x}_i}{\partial q_k}$

2.2 Deducción de las ecuaciones

Partimos de la definición

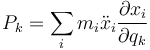
$P_k = \sum_i m_i \ddot{x}_i\frac{\partial x_i}{\partial q_k}$

Aplicamos la derivada de un producto

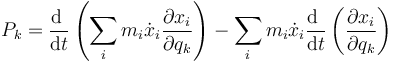
$P_k = \frac{\mathrm{d}\ }{\mathrm{d}t}\left(\sum_i m_i\dot{x}_i\frac{\partial x_i}{\partial q_k}\right)-\sum_i m_i\dot{x}_i\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial x_i}{\partial q_k}\right)$

Sustituimos aquí las dos identidades obtenidas anteriormente

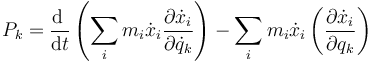
$P_k = \frac{\mathrm{d}\ }{\mathrm{d}t}\left(\sum_i m_i\dot{x}_i\frac{\partial \dot{x}_i}{\partial \dot{q}_k}\right)-\sum_i m_i\dot{x}_i\left(\frac{\partial \dot{x}_i}{\partial q_k}\right)$

Si introducimos aquí la energía cinética K (que en mecánica analítica se escribe casi exclusivamente como T, pero por ser consistentes con la notación de otras páginas de este curso)

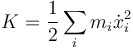
$K=\frac{1}{2}\sum_i m_i\dot{x}_i^2$

la identidad anterior equivale a

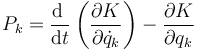
$P_k = \frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial K}{\partial \dot{q}_k}\right)-\frac{\partial K}{\partial q_k}$

Llevando esto al principio de D'Alembert nos queda una primera versión de las ecuaciones de Lagrange

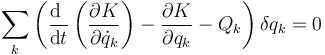
$\sum_k\left(\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial K}{\partial \dot{q}_k}\right)-\frac{\partial K}{\partial q_k}-Q_k\right)\delta q_k=0$

donde las $Q k$ no incluyen las fuerzas de reacción vincular. A esta ecuación hay que añadir las r ecuaciones de vínculo

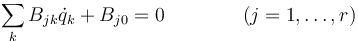
$\sum_k B_{jk}\dot{q}_k+B_{j0}=0\qquad\qquad(j=1,\ldots,r)$

que permiten relacionar los desplazamientos virtuales

$\sum_k B_{jk}\delta q_k=0\qquad\qquad(j=1,\ldots,r)$

2.3 Coordenadas independientes

Cuando todos os vínculos son holónomos, es posible (en teoría; en la práctica pueden resultar ecuaciones irresolubles) elegir un sistema mínimo de tantas coordenadas como grados de libertad de forma que todos los vínculos se satisfagan automáticamente.

En ese caso, todos los desplazamientos virtuales son independientes y cada coeficiente se debe anular por separado, resultando las ecuaciones de Lagrange (o de Euler-Lagrange)

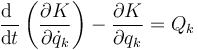
$\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial K}{\partial \dot{q}_k}\right)-\frac{\partial K}{\partial q_k}=Q_k$

Coordenadas polares

Las ecuaciones de Lagrange proporcionan un método para calcular las componentes de la aceleración en diferentes sistemas de coordenadas sin tener que complicarse con vectores de la base y sus derivadas.

Consideremos una partícula que se mueve en el plano OXY, estando su posición expresada en coordenadas polares de manera que

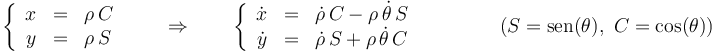
$\left\{\begin{array}{rcl}x & = & \rho\,C \\ y & = & \rho\,S\end{array}\right.\qquad\Rightarrow\qquad \left\{\begin{array}{rcl}\dot{x} & = & \dot{\rho}\,C-\rho\,\dot{\theta}\,S \\ \dot{y} & = & \dot{\rho}\,S+\rho\,\dot{\theta}\,C\end{array}\right.\qquad\qquad \left(S=\mathrm{sen}(\theta),\ C=\cos(\theta)\right)$

Esto da la energía cinética

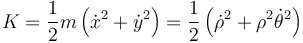
$K=\frac{1}{2}m\left(\dot{x}^2+\dot{y}^2\right)=\frac{1}{2}\left(\dot{\rho}^2+\rho^2\dot{\theta}^2\right)$

Aplicamos ahora la ecuación de Lagrange a la coordenada radial

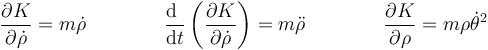
$\frac{\partial{K}}{\partial \dot{\rho}}=m\dot{\rho}\qquad\qquad\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial{K}}{\partial \dot{\rho}}\right)=m\ddot{\rho}\qquad\qquad \frac{\partial{K}}{\partial \rho}=m\rho\dot{\theta}^2$

lo que nos da

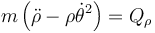
$m\left(\ddot{\rho}-\rho{\dot{\theta}^2}\right)=Q_\rho$

Por tratarse la coordenada de una distancia la fuerza generalizada es simplemente la fuerza en dicha dirección, es decir

$m\left(\ddot{\rho}-\rho{\dot{\theta}^2}\right)=F_\rho\qquad\rightarrow\qquad a_\rho=\ddot{\rho}-\rho{\dot{\theta}^2}$

Operamos igualmente para la coordenada angular

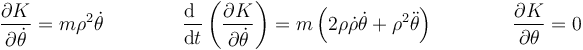
$\frac{\partial{K}}{\partial \dot{\theta}}=m\rho^2\dot{\theta}\qquad\qquad\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial{K}}{\partial \dot{\theta}}\right)=m\left(2\rho\dot{\rho}\dot{\theta}+\rho^2\ddot{\theta}\right)\qquad\qquad \frac{\partial{K}}{\partial \theta}=0$

y obtenemos

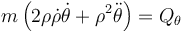
$m\left(2\rho\dot{\rho}\dot{\theta}+\rho^2\ddot{\theta}\right)=Q_\theta$

Por tratarse de un ángulo, la fuerza generalizada representa el momento de las fuerzas que actúan sobre la partícula y es igual al producto de la fuerza acimutal por el brazo del par, que en este caso es la distancia al origen

$m\left(2\rho\dot{\rho}\dot{\theta}+\rho^2\ddot{\theta}\right)=\rho F_\theta\qquad\Rightarrow\qquad a_\theta=2\dot{\rho}\dot{\theta}+\rho\ddot{\theta}$

2.4 Fuerzas de reacción vincular

Si no todos los vínculos son holónomos o si deseamos hallar las fuerzas de reacción generalizadas debemos usar un número de coordenadas generalizadas superior al de grados de libertad.

A cada vínculo le corresponde una fuerza de reacción generalizada que podemos reintroducir en el sistema como una fuerza aplicada mediante los multiplicadores de Lagrange

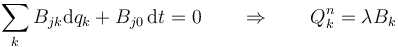
$\sum_k B_{jk} \mathrm{d}q_k+B_{j0}\,\mathrm{d} t = 0\qquad\Rightarrow\qquad Q^n_k=\lambda B_k$

Al incluir cada una de estas fuerzas deja de aplicarse el vínculo correspondiente, aumentando en uno el número de diferenciales independientes y por tanto el número de ecuaciones

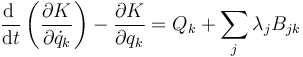
$\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial K}{\partial \dot{q}_k}\right)-\frac{\partial K}{\partial q_k}=Q_k+\sum_j \lambda_j B_{jk}$

3 Fuerzas conservativas

3.1 Lagrangiana

Las fuerzas conservativas son aquellas que realizan un trabajo independiente del camino. Para estas fuerzas puede definirse una energía potencial U (habitualmente denotada también como V) tal que las componentes cartesianas de la fuerza equivalen al gradiente de la energía potencial cambiado de signo.

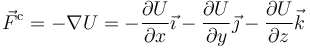
$\vec{F}^\mathrm{c}=-\nabla U = -\frac{\partial U}{\partial x}\vec{\imath}- \frac{\partial U}{\partial y}\vec{\jmath}-\frac{\partial U}{\partial z}\vec{k}$

Separando por componentes cartesianas

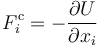
$F^\mathrm{c}_i=-\frac{\partial U}{\partial x_i}$

La fuerza generalizada correspondiente a una fuerza conservativa vendrá dada por la expresión

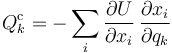
$Q^\mathrm{c}_k = -\sum_i \frac{\partial U}{\partial x_i}\,\frac{\partial x_i}{\partial q_k}$

pero, por la regla de la cadena, esta expresión equivale a

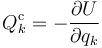
$Q_k^\mathrm{c} = -\frac{\partial U}{\partial q_k}$

Sobre un sistema actuarán en general fuerzas cosnervativas (como el peso) y fuerzas no conservativas (como el rozamiento), además de las de reacción vincular. Para las conservativas podemos emplear esta relación (tomando como energía potencial total la suma de las diferentes energías potenciales) y transformar la ecuación de Lagrange

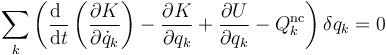
$\sum_k \left(\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial K}{\partial \dot{q}_k}\right)-\frac{\partial K}{\partial q_k}+\frac{\partial U}{\partial q_k}-Q_k^\mathrm{nc}\right)\delta q_k=0$

Definimos la función lagrangiana del sistema

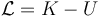
$\mathcal{L}=K-U\,$

Esta función depende de las coordenadas generalizadas y del tiempo (que aparecen en K y U), pero también de las velocidades generalizadas, que en principio aparecen solo en K.

Empleando la notación habitual en los libros de mecánica analítica sería 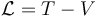$\mathcal{L}=T-V$ .

Con ayuda de esta función las fuerzas conservativas puede incorporarse en los primeros términos

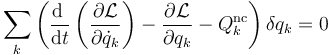
$\sum_k \left(\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial \mathcal{L}}{\partial \dot{q}_k}\right)-\frac{\partial \mathcal{L}}{\partial q_k}-Q_k^\mathrm{nc}\right)\delta q_k=0$

Si además las coordenadas son independientes se anulan los coeficientes, resultando las ecuaciones de Lagrange (una por cada coordenada):

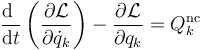
$\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial \mathcal{L}}{\partial \dot{q}_k}\right)-\frac{\partial \mathcal{L}}{\partial q_k}=Q_k^\mathrm{nc}$

y, si no hay presentes fuerzas no conservativas

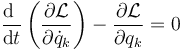
$\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial \mathcal{L}}{\partial \dot{q}_k}\right)-\frac{\partial \mathcal{L}}{\partial q_k}=0$

Esta es la forma más simple de las ecuaciones de Lagrange y dado que aparecen así en muchos problemas, es tentador pensar que son universalmente válidas, pero hay que tener en mente siempre que esta expresión solo vale en ausencia de fuerzas no conservativas y si todas las coordenadas son independientes.

Oscilador armónico

Como caso muy simple de aplicación de las ecuaciones de Lagrange tenemos el ejemplo de un socilador armónico en una dimensión. Para este sistema

$K=\frac{1}{2}m\dot{x}^2\qquad\qquad U=\frac{1}{2}k(x-\ell_0)^2\qquad\qquad \mathcal{L}=K-U=\frac{1}{2}m\dot{x}^2-\frac{1}{2}k(x-\ell_0)^2$

lo que da la ecuación de movimiento

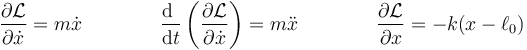
$\frac{\partial \mathcal{L}}{\partial\dot{x}}=m\dot{x}\qquad\qquad \frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial \mathcal{L}}{\partial\dot{x}}\right)=m\ddot{x}\qquad\qquad \frac{\partial \mathcal{L}}{\partial x}=-k(x-\ell_0)$

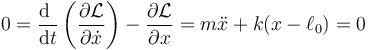
$0=\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial \mathcal{L}}{\partial \dot{x}}\right)-\frac{\partial \mathcal{L}}{\partial x}=m\ddot{x}+k(x-\ell_0)=0$

Péndulo simple

Para el caso de un péndulo simple podemos emplear la energía cinética calculada previamente

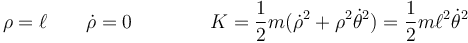
$\rho=\ell\qquad\dot{\rho}=0\qquad\qquad K=\frac{1}{2}m(\dot{\rho}^2+\rho^2\dot{\theta}^2)=\frac{1}{2}m\ell^2\dot{\theta}^2$

y para la energía potencial, si tomamos el eje X como vertical y hacia abajo

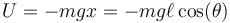
$U=-mgx=-mg\ell \cos(\theta)$

Llegamos entonces a la lagrangiana

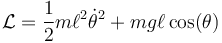
$\mathcal{L}=\frac{1}{2}m\ell^2 \dot{\theta}^2+mg\ell\cos(\theta)$

y de aquí a la ecuación de movimiento

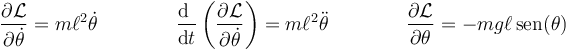
$\frac{\partial \mathcal{L}}{\partial\dot{\theta}}=m\ell^2\dot{\theta}\qquad\qquad \frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial \mathcal{L}}{\partial\dot{\theta}}\right)=m\ell^2\ddot{\theta}\qquad\qquad \frac{\partial \mathcal{L}}{\partial \theta}=-mg\ell\,\mathrm{sen}(\theta)$

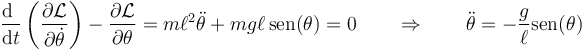
$\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial \mathcal{L}}{\partial \dot{\theta}}\right)-\frac{\partial \mathcal{L}}{\partial \theta}=m\ell^2\ddot{\theta}+mg\ell\,\mathrm{sen}(\theta)=0\qquad\Rightarrow\qquad \ddot{\theta}=-\frac{g}{\ell}\mathrm{sen}(\theta)$

En un caso más general, con fuerzas no conservativas y considerando las fuerzas de reacción como fuerzas aplicadas quedaría la forma

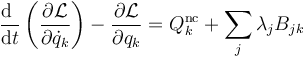
$\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial \mathcal{L}}{\partial \dot{q}_k}\right)-\frac{\partial \mathcal{L}}{\partial q_k}=Q^\mathrm{nc}_k+\sum_j \lambda_j B_{jk}$

3.2 Cálculo de las fuerzas de reacción

Incluso en los casos de coordenadas independientes y ausencia de fuerzas no conservativas puede interesarnos la determinación de las fuerzas de reacción asociadas a un vínculo de la forma

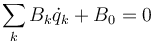
$\sum_k B_k\dot{q}_k+B_0=0\,$

En ese caso, el procedimiento consiste en desvincular esta ligadura, suponiendo una fuerza de reacción vincular que produce el mismo efecto. En ese caso, tenemos una coordenada independiente más, y el conjunto se ve modificado con la introducción de esta fuerza de reacción

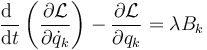
$\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial \mathcal{L}}{\partial \dot{q}_k}\right)-\frac{\partial \mathcal{L}}{\partial q_k}=\lambda B_k$

En la mayoría de los casos, las coordenadas generalizadas se eligen precisamente para que los vínculos se reduzcan a identidades triviales, como $q n = b = cte$ . En ese caso, la fuerza de reacción vincular se reduce a una sola componente (en la dirección de $q n$ ) cuyo valor es justamente el multiplicador de Lagrange.

Tensión del péndulo simple

Tras plantear las ecuaciones del péndulo simple, podemos determinar la tensión desvinculando la ligadura 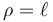$\rho=\ell$ . Es decir, volvemos a escribir la lagrangiana, suponiendo ahora que $ρ$ es variable

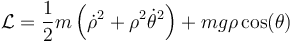
$\mathcal{L}=\frac{1}{2}m\left(\dot{\rho}^2+\rho^2\dot{\theta}^2\right)+mg\rho\cos(\theta)$

Escribimos la ecuación de movimiento para la coordenada radial

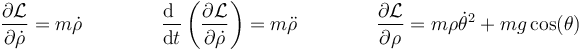
$\frac{\partial \mathcal{L}}{\partial\dot{\rho}}=m\dot{\rho}\qquad\qquad \frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial \mathcal{L}}{\partial\dot{\rho}}\right)=m\ddot{\rho}\qquad\qquad \frac{\partial \mathcal{L}}{\partial \rho}=m\rho\dot{\theta}^2+mg\cos(\theta)$

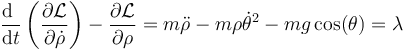
$\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial \mathcal{L}}{\partial \dot{\rho}}\right)-\frac{\partial \mathcal{L}}{\partial \rho}=m\ddot{\rho}-m\rho\dot{\theta}^2-mg\cos(\theta)=\lambda$

Si aplicamos ahora que la fuerza de reacción es tal que la ecuación del vínculo se sigue cumpliendo, 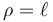$\rho=\ell$ y la segunda derivada se anula

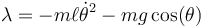
$\lambda = -m\ell\dot{\theta}^2-mg\cos(\theta)$

En este caso, el multiplicador de Lagrange nos da la componente de la fuerza en la dirección y sentido en que aumenta $ρ$ . Resulta negativa, ya que la tensión es radial, pero hacia adentro.

Por otro lado, a partir de la ley de conservación de la energía mecánica, podemos hallar 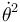$\dot{\theta}^2$ en función de $θ$ y sustituir aquí.

3.3 Potenciales dependientes de la velocidad

El concepto de potencial puede generalizarse a algunas fuerzas dependientes de la velocidad, como la fuerza magnética de Lorentz 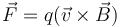$\vec{F}=q(\vec{v}\times\vec{B})$ . Para estas fuerzas puede definirse un potencial que cumple

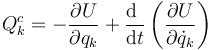
$Q^c_k = -\frac{\partial U}{\partial q_k}+\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial U}{\partial \dot{q}_k}\right)$

Si se cumple esta condición, las ecuaciones de Lagrange siguen siendo válidas

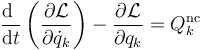
$\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial \mathcal{L}}{\partial \dot{q}_k}\right)-\frac{\partial \mathcal{L}}{\partial q_k}=Q_k^\mathrm{nc}$

donde ahora las velocidades aparecen tanto en la energía cinética como en la potencial.

Sistema en rotación

Un caso en el que se puede usar esta formulación es el correspondiente a un sistema de referencia en rotación uniforme (como puede ser el propio planeta Tierra). Es sabido que en este sistema una partícula parece experimentar las fuerzas ficticias centrífuga y de Coriolis.

$\vec{F}_c=-m\vec{\omega}\times(\vec{\omega}\times\vec{r})\qquad\qquad \vec{F}_C=-2m\vec{\omega}\times\vec{v}$

La fuerza de Coriolis es dependiente de la velocidad medida en el sistema de referencia en rotación. Por ello, sin necesidad de modificar nada, la lagrangiana calculada en un sistema de referencia fijo puede reinterpretarse como la resta a una energía cinética (medida en el sistema en rotación) de una energía potencial dependiente de las velocidades.

Consideremos el caso plano, con un sistema que gira con velocidad angular constante Ω alrededor del eje OZ. En ese caso las coordenadas (x,y) del sistema fijo se relacionan con las (X,Y) del sistema móvil a través de la matriz de rotación y de la fórmula de Poisson

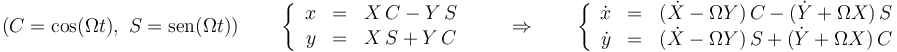
$\left(C=\cos(\Omega t),\ S=\mathrm{sen}(\Omega t)\right)\qquad\left\{\begin{array}{rcl}x&=&X\,C-Y\,S \\ y & = & X\,S+Y\,C\end{array}\right.\qquad\Rightarrow\qquad \left\{\begin{array}{rcl}\dot{x}&=&(\dot{X}-\Omega Y)\,C-(\dot{Y}+\Omega X)\,S \\ \dot{y} & = & (\dot{X}-\Omega Y)\,S+(\dot{Y}+\Omega X)\,C\end{array}\right.$

lo que nos da la energía cinética

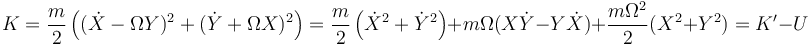
$K=\frac{m}{2}\left((\dot{X}-\Omega Y)^2+(\dot{Y}+\Omega X)^2\right)= \frac{m}{2}\left(\dot{X}^2+\dot{Y}^2\right)+m\Omega(X\dot{Y}-Y\dot{X})+\frac{m\Omega^2}{2}(X^2+Y^2)=K'-U$

siendo el potencial efectivo, dependiente de la velocidad

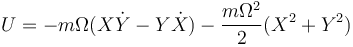
$U=-m\Omega(X\dot{Y}-Y\dot{X})-\frac{m\Omega^2}{2}(X^2+Y^2)$

A partir de este potencial se deducen tanto la fuerza centrífuga como la de Coriolis.

$\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial U}{\partial \dot{X}}\right) -\frac{\partial U}{\partial X}=-m\Omega^2 X -2m\Omega\dot{Y}\qquad\qquad \frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial U}{\partial \dot{Y}}\right) -\frac{\partial U}{\partial Y}=-m\Omega^2 Y + 2m\Omega\dot{X}$

@@ Línea 69: / Línea 69: @@
 <center><math>P_k = \frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial K}{\partial \dot{q}_k}\right)-\frac{\partial K}{\partial q_k}</math></center>
-Llevando esto al principio de D'Alembert nos queda una primera ecuación de las ecuaciones de Lagrange
+Llevando esto al principio de D'Alembert nos queda una primera versión de las ecuaciones de Lagrange
 <center><math>\sum_k\left(\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial K}{\partial \dot{q}_k}\right)-\frac{\partial K}{\partial q_k}-Q_k\right)\delta q_k=0</math></center>
@@ Línea 84: / Línea 84: @@
 Cuando todos os vínculos son holónomos, es posible (en teoría; en la práctica pueden resultar ecuaciones irresolubles) elegir un sistema mínimo de tantas coordenadas como grados de libertad de forma que todos los vínculos se satisfagan automáticamente.
-En ese caso, todos los desplazamientos virtuales son independientes y cada coeficiente se debe anular por separado, resultando las ecuaciones
+En ese caso, todos los desplazamientos virtuales son independientes y cada coeficiente se debe anular por separado, resultando las ecuaciones de Lagrange (o de Euler-Lagrange)
 <center><math>\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial K}{\partial \dot{q}_k}\right)-\frac{\partial K}{\partial q_k}=Q_k</math></center>
@@ Línea 173: / Línea 173: @@
 Si además las coordenadas son independientes se anulan los coeficientes, resultando las ecuaciones de Lagrange (una por cada coordenada):
-<center><math>\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial \mathcal{L}}{\partial \dot{q}_k}\right)-\frac{\partial \mathcal{L}}{\partial q_k}-Q_k^\mathrm{nc}=0</math></center>
+<center><math>\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial \mathcal{L}}{\partial \dot{q}_k}\right)-\frac{\partial \mathcal{L}}{\partial q_k}=Q_k^\mathrm{nc}</math></center>
 y, si no hay presentes fuerzas no conservativas
@@ Línea 277: / Línea 277: @@
 <center><math>K=\frac{m}{2}\left((\dot{X}-\Omega Y)^2+(\dot{Y}+\Omega X)^2\right)=
-\frac{m}{2}\left(\dot{X}^2+\dot{Y}^2\right)+m\Omega(X\dot{Y}-Y\dot{X})+\frac{m\Omega^2}{2}(X^2+Y^2)=K'-U_\mathrm{ef}</math></center>
+\frac{m}{2}\left(\dot{X}^2+\dot{Y}^2\right)+m\Omega(X\dot{Y}-Y\dot{X})+\frac{m\Omega^2}{2}(X^2+Y^2)=K'-U</math></center>
 siendo el potencial efectivo, dependiente de la velocidad
-<center><math>U_\mathrm{ef}=-m\Omega(X\dot{Y}-Y\dot{X})-\frac{m\Omega^2}{2}(X^2+Y^2)</math></center>
+<center><math>U=-m\Omega(X\dot{Y}-Y\dot{X})-\frac{m\Omega^2}{2}(X^2+Y^2)</math></center>
 A partir de este potencial se deducen tanto la fuerza centrífuga como la de Coriolis.

Ecuaciones de Lagrange (CMR)

De Laplace

última version al 15:08 22 ene 2017

Contenido

1 Introducción

2 Ecuaciones de Euler-Lagrange

2.1 Dos identidades utiles

2.2 Deducción de las ecuaciones

2.3 Coordenadas independientes

2.4 Fuerzas de reacción vincular

3 Fuerzas conservativas

3.1 Lagrangiana

3.2 Cálculo de las fuerzas de reacción

3.3 Potenciales dependientes de la velocidad

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES