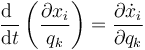Ecuaciones de Lagrange (CMR)
De Laplace
| Línea 37: | Línea 37: | ||
Por otro lado, si hallamos la derivada tota respecto al tiempo de la derivada parcial | Por otro lado, si hallamos la derivada tota respecto al tiempo de la derivada parcial | ||
| - | <center><math>\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial x_i}{q_k}\right)=\sum_p\frac{\partial\ }{\partial q_k}\left(\frac{\partial x_i}{q_k}\right)+\frac{\partial\ }{\partial t}\left(\frac{\partial x_i}{q_k}\right)</math></center> | + | <center><math>\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial x_i}{q_k}\right)=\sum_p\frac{\partial\ }{\partial q_k}\left(\frac{\partial x_i}{\partial q_k}\right)+\frac{\partial\ }{\partial t}\left(\frac{\partial x_i}{\partial q_k}\right)</math></center> |
Por las propiedades de las derivadas parciales se puede invertir el orden de cada derivada cruzada | Por las propiedades de las derivadas parciales se puede invertir el orden de cada derivada cruzada | ||
| - | <center><math>\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial x_i}{q_k}\right)=\frac{\partial \ }{q_k}\left(\sum_p\frac{\partial x_i}{q_p}+\frac{\partial x_i}{\partial t}\right)=\frac{\partial\ }{\partial q_k}\left(\frac{\mathrm{d}x_i}{\mathrm{d}t}\right)</math></center> | + | <center><math>\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial x_i}{\partial q_k}\right)=\frac{\partial \ }{q_k}\left(\sum_p\frac{\partial x_i}{\partial q_p}+\frac{\partial x_i}{\partial t}\right)=\frac{\partial\ }{\partial q_k}\left(\frac{\mathrm{d}x_i}{\mathrm{d}t}\right)</math></center> |
Es decir, resulta la identidad | Es decir, resulta la identidad | ||
Revisión de 20:30 14 ene 2017
Contenido |
1 Introducción
Al introducir las coordenadas generalizadas llegamos a que el principio de D'Alembert puede escribirse en la forma
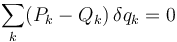
En el caso particular importante de que todos los vínculos sean holónomos y podamos definir 3N-r coordenadas generalizadas intependientes, cada uno de los coeficientes debe anularse por separado y obtenemos el sistema de ecuaciones
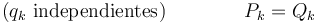
Aquí las cantidades Qk son las fuerzas generalizadas
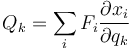
a las que se le puede dar una interpretación relativamente simple: son las componentes (en un sentido amplio) de las fuerzas que pueden producir un cambio en la coordenada qk. Si esta coordenada es cartesiana, Qk representa una fuerza usual; si es un ángulo, representa el momento de una fuerza (que es el que produce un giro) y así sucesivamente.
Los términos Pk no tienen una interpretación inmediata. Se definen como
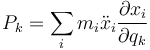
y podemos decir que − Pk representa una fuerza de inercia generalizada, pero esta interpretación no aporta mucho, ya que esa fuerza de inercia requiere hallar la aceleración de las partículas, lo que es precisamente uno de los objetivos de la dinámica, por lo que no se pueden tratar como fuerzas aplicada.
En lo que sigue deduciremos expresiones alternativas para Pk que proporcionan un método sistemático para la determinación de estas fuerzas de inercia generalizadas que no requiera conocer la solución del problema que queremos resolver.
2 Ecuaciones de Euler-Lagrange
2.1 Dos identidades utiles
Definimos un conjunto de coordenadas generalizadas qk de manera que las coordenadas cartesianas de las diferentes partículas se escriben
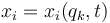
A partir de las relaciones entre coordenadas hallamos la relación entre velocidades derivando
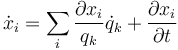
La velocidad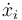 
es una función de las coodenadas generalizadas, de las velocidades generalizadas y del tiempo. De la expresión anterior se deduce que
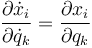
Por otro lado, si hallamos la derivada tota respecto al tiempo de la derivada parcial
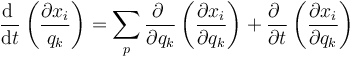
Por las propiedades de las derivadas parciales se puede invertir el orden de cada derivada cruzada
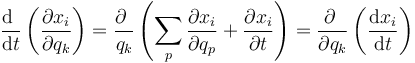
Es decir, resulta la identidad
