Entrar Página Discusión Historial Go to the site toolbox

Espiral logarítmica (GIE)

De Laplace

(Diferencias entre revisiones)
(→Tiempo de impacto)
 
(7 ediciones intermedias no se muestran.)
Línea 2: Línea 2:
Una partícula describe una ''espiral logarítmica'' a partir de <math>t=0</math> de manera que, en el SI y empleando coordenadas polares,
Una partícula describe una ''espiral logarítmica'' a partir de <math>t=0</math> de manera que, en el SI y empleando coordenadas polares,
-
<center><math>\rho = 240-48t\qquad\qquad \varphi = -0.75\ln\left(1.00-0.20t\right)</math></center>
+
<center><math>\rho = 240-48t\qquad\qquad \theta = -0.75\ln\left(1.00-0.20t\right)</math></center>
# Halle la velocidad en cada instante.
# Halle la velocidad en cada instante.
Línea 8: Línea 8:
# ¿Cuánto tiempo tarda la partícula en llegar al origen de coordenadas? ¿Cuántas vueltas alrededor del origen da en ese tiempo?
# ¿Cuánto tiempo tarda la partícula en llegar al origen de coordenadas? ¿Cuántas vueltas alrededor del origen da en ese tiempo?
# Halle la aceleración para cada instante, así como sus componentes intrínsecas
# Halle la aceleración para cada instante, así como sus componentes intrínsecas
-
# Calcule los vectores tangente y normal a la trayectoria en cada punto de ésta, en función de la base <math>\{\vec{u}_\rho,\vec{u}_\varphi\}</math>
+
# Calcule los vectores tangente y normal a la trayectoria en cada punto de ésta, en función de la base <math>\{\vec{u}_\rho,\vec{u}_\theta\}</math>
# Calcule el radio de curvatura como función del tiempo.
# Calcule el radio de curvatura como función del tiempo.
Línea 14: Línea 14:
La fórmula para la velocidad en coordenadas polares viene dada por
La fórmula para la velocidad en coordenadas polares viene dada por
-
<center><math>\vec{v} = \dot{\rho}\vec{u}_\rho + \rho\dot{\varphi}\vec{u}_\varphi</math></center>
+
<center><math>\vec{v} = \dot{\rho}\vec{u}_\rho + \rho\dot{\theta}\vec{u}_\theta</math></center>
siendo en este caso
siendo en este caso
<center><math>\dot{\rho} = \frac{\mathrm{d}\rho}{\mathrm{d}t} = -48\,\frac{\mathrm{m}}{\mathrm{s}}\qquad\qquad  
<center><math>\dot{\rho} = \frac{\mathrm{d}\rho}{\mathrm{d}t} = -48\,\frac{\mathrm{m}}{\mathrm{s}}\qquad\qquad  
-
\dot{\varphi}=\frac{\mathrm{d}\varphi}{\mathrm{d}t}=\frac{0.15}{1.00-0.20t}\mathrm{s}^{-1}</math></center>
+
\dot{\theta}=\frac{\mathrm{d}\theta}{\mathrm{d}t}=\frac{0.15}{1.00-0.20t}\mathrm{s}^{-1}</math></center>
lo que nos da la velocidad
lo que nos da la velocidad
-
<center><math>\vec{v}=\left(-48\,\vec{u}_\rho}+\frac{0.15(240-48t)}{1.00-0.20t}\vec{u}_\varphi}\right)\frac{\mathrm{m}}{\mathrm{s}}</math></center>
+
<center><math>\vec{v}=\left(-48\,\vec{u}_\rho+\frac{0.15(240-48t)}{1.00-0.20t}\vec{u}_\theta\right)\frac{\mathrm{m}}{\mathrm{s}}</math></center>
pero
pero
Línea 31: Línea 31:
así que queda simplemente
así que queda simplemente
-
<center><math>\vec{v}=(-48\vec{u}_\rho+36\vec{u}_\varphi)\frac{\mathrm{m}}{\mathrm{s}}</math></center>
+
<center><math>\vec{v}=(-48\vec{u}_\rho+36\vec{u}_\theta)\frac{\mathrm{m}}{\mathrm{s}}</math></center>
Hay que señalar que esta velocidad ''depende del tiempo''. Aunque las componentes son constantes, los vectores de la base son dependientes del tiempo, ya que van girando con la partícula en su movimiento.
Hay que señalar que esta velocidad ''depende del tiempo''. Aunque las componentes son constantes, los vectores de la base son dependientes del tiempo, ya que van girando con la partícula en su movimiento.
 +
 +
<center>[[Archivo:nautilus-03.gif]]</center>
 +
==Rapidez instantánea==
==Rapidez instantánea==
Una vez que tenemos la velocidad instantánea, calculamos la rapidez hallando su módulo.
Una vez que tenemos la velocidad instantánea, calculamos la rapidez hallando su módulo.
-
<center><math>|\vec{v}| = \sqrt{v_\rho^2+v_\varphi^2} = \sqrt{48^2+36^2}\,\frac{\mathrm{m}}{\mathrm{s}} = 60\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
+
<center><math>|\vec{v}| = \sqrt{v_\rho^2+v_\theta^2} = \sqrt{48^2+36^2}\,\frac{\mathrm{m}}{\mathrm{s}} = 60\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
El movimiento es con rapidez constante y por tanto uniforme.
El movimiento es con rapidez constante y por tanto uniforme.
Línea 45: Línea 48:
<center><math>240-48t_\mathrm{i} = 0\qquad\Rightarrow\qquad t = 5\,\mathrm{s}</math></center>
<center><math>240-48t_\mathrm{i} = 0\qquad\Rightarrow\qquad t = 5\,\mathrm{s}</math></center>
-
El número de vueltas lo obtenemos calculando la variación en la coordenada <math>\varphi</math>. Cuando este ángulo varía en <math>2\pi</math> quiere decir que se ha dado una vuelta. Si varía en <math>4\pi</math> son dos vueltas y así sucesivamente. El número de vueltas total será
+
El número de vueltas lo obtenemos calculando la variación en la coordenada <math>\theta</math>. Cuando este ángulo varía en <math>2\pi</math> quiere decir que se ha dado una vuelta. Si varía en <math>4\pi</math> son dos vueltas y así sucesivamente. El número de vueltas total será
-
<center><math>n = \frac{\Delta\varphi}{2\pi}=\frac{1}{2\pi}\left(-0.75\ln\left(1.00-0.20t\right)\right|_{0\,\mathrm{s}}^{5\,\mathrm{s}}</math></center>
+
<center><math>n = \frac{\Delta\theta}{2\pi}=\frac{1}{2\pi}\left.\left(-0.75\ln\left(1.00-0.20t\right)\right)\right|_{0\,\mathrm{s}}^{5\,\mathrm{s}}</math></center>
Pero
Pero
Línea 63: Línea 66:
La expresión de la aceleración en coordenadas polares es
La expresión de la aceleración en coordenadas polares es
-
<center><math>\vec{a} = (\ddot{\rho}-\rho\dot{\varphi}^2)\vec{u}_\rho+(\rho\ddot{\varphi}+2\dot{\rho}\dot{\varphi})\vec{u}_\varphi</math></center>
+
<center><math>\vec{a} = (\ddot{\rho}-\rho\dot{\theta}^2)\vec{u}_\rho+(\rho\ddot{\theta}+2\dot{\rho}\dot{\theta})\vec{u}_\theta</math></center>
donde, en este caso
donde, en este caso
<center><math>\ddot{\rho}=0\,\frac{\mathrm{m}}{\mathrm{s}^2}</math>{{qquad}}{{qquad}}<math>
<center><math>\ddot{\rho}=0\,\frac{\mathrm{m}}{\mathrm{s}^2}</math>{{qquad}}{{qquad}}<math>
-
\rho\dot{\varphi}^2 = \overbrace{(\rho\dot{\varphi})}^{36}\dot{\varphi}=\frac{5.4}{1.00-0.20t}\,\frac{\mathrm{m}}{\mathrm{s}^2}</math>{{qquad}}{{qquad}}
+
\rho\dot{\theta}^2 = \overbrace{(\rho\dot{\theta})}^{36}\dot{\theta}=\frac{5.4}{1.00-0.20t}\,\frac{\mathrm{m}}{\mathrm{s}^2}</math>{{qquad}}{{qquad}}
-
<math>\rho\ddot{\varphi} = \frac{7.2}{1.00-0.20t}\,\frac{\mathrm{m}}{\mathrm{s}^2}</math>{{qquad}}{{qquad}}
+
<math>\rho\ddot{\theta} = \frac{7.2}{1.00-0.20t}\,\frac{\mathrm{m}}{\mathrm{s}^2}</math>{{qquad}}{{qquad}}
-
<math>2\dot{\rho}\dot{\varphi} = -\frac{14.4}{1.00-0.20t}\,\frac{\mathrm{m}}{\mathrm{s}^2}</math>
+
<math>2\dot{\rho}\dot{\theta} = -\frac{14.4}{1.00-0.20t}\,\frac{\mathrm{m}}{\mathrm{s}^2}</math>
</center>
</center>
Reuniendo todo esto nos queda
Reuniendo todo esto nos queda
-
<center><math>\vec{a} = -\frac{5.4\vec{u}_\rho+7.2\vec{u}_\varphi}{1.00-0.20t}\,\frac{\mathrm{m}}{\mathrm{s}^2}</math></center>
+
<center><math>\vec{a} = -\frac{5.4\vec{u}_\rho+7.2\vec{u}_\theta}{1.00-0.20t}\,\frac{\mathrm{m}}{\mathrm{s}^2}</math></center>
En este caso particular, no obstante, hubiera sido más fácil calcular la aceleración como la derivada de la velocidad respecto al tiempo, aprovechando que las componentes de la velocidad son constantes.
En este caso particular, no obstante, hubiera sido más fácil calcular la aceleración como la derivada de la velocidad respecto al tiempo, aprovechando que las componentes de la velocidad son constantes.
-
<center><math>\vec{v}=(-48\vec{u}_\rho+36\vec{u}_\varphi)\frac{\mathrm{m}}{\mathrm{s}}</math></center>
+
<center><math>\vec{v}=(-48\vec{u}_\rho+36\vec{u}_\theta)\frac{\mathrm{m}}{\mathrm{s}}</math>{{qquad}}{{qquad}}<math>\vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=\left(-48\frac{\mathrm{d}\vec{u}_\rho}{\mathrm{d}t}+36\frac{\mathrm{d}\vec{u}_\theta}{\mathrm{d}t}\right)\frac{\mathrm{m}}{\mathrm{s}^2}</math></center>
-
 
+
-
<center><math>\vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=\left(-48\frac{\mathrm{d}\vec{u}_\rho}{\mathrm{d}t}+36\frac{\mathrm{d}\vec{u}_\varphi}{\mathrm{d}t}\right)\frac{\mathrm{m}}{\mathrm{s}^2}</math></center>
+
donde
donde
-
<center><math>\frac{\mathrm{d}\vec{u}_\rho}{\mathrm{d}t} = \dot{\varphi}\vec{u}_\varphi=\left(\frac{0.15}{1.00-0.20t}\vec{u}_\varphi\right)\frac{1}{\mathrm{s}}\qquad\qquad \frac{\mathrm{d}\vec{u}_\varphi}{\mathrm{d}t} = -\dot{\varphi}\vec{u}_\rho=-\left(\frac{0.15}{1.00-0.20t}\vec{u}_\rho\right)\frac{1}{\mathrm{s}}</math></center>
+
<center><math>\frac{\mathrm{d}\vec{u}_\rho}{\mathrm{d}t} = \dot{\theta}\vec{u}_\theta=\left(\frac{0.15}{1.00-0.20t}\vec{u}_\theta\right)\frac{1}{\mathrm{s}}\qquad\qquad \frac{\mathrm{d}\vec{u}_\theta}{\mathrm{d}t} = -\dot{\theta}\vec{u}_\rho=-\left(\frac{0.15}{1.00-0.20t}\vec{u}_\rho\right)\frac{1}{\mathrm{s}}</math></center>
lo que nos da la aceleración
lo que nos da la aceleración
-
<center><math>\vec{a}=\frac{0.15}{1.00-0.20t}\left(-48\vec{u}_\varphi-36\vec{u}_\rho\right)\frac{\mathrm{m}}{\mathrm{s}^2}=-\frac{5.4\vec{u}_\rho+7.2\vec{u}_\varphi}{1.00-0.20t}\,\frac{\mathrm{m}}{\mathrm{s}^2}</math></center>
+
<center><math>\vec{a}=\frac{0.15}{1.00-0.20t}\left(-48\vec{u}_\theta-36\vec{u}_\rho\right)\frac{\mathrm{m}}{\mathrm{s}^2}=-\frac{5.4\vec{u}_\rho+7.2\vec{u}_\theta}{1.00-0.20t}\,\frac{\mathrm{m}}{\mathrm{s}^2}</math></center>
===Aceleración tangencial===
===Aceleración tangencial===
Línea 99: Línea 100:
Si la aceleración tangencial es nula, toda la aceleración es normal, por lo que
Si la aceleración tangencial es nula, toda la aceleración es normal, por lo que
-
<center><math>\vec{a}_n = -\frac{5.4\vec{u}_\rho+7.2\vec{u}_\varphi}{1.00-0.20t}\,\frac{\mathrm{m}}{\mathrm{s}^2}</math></center>
+
<center><math>\vec{a}_n = -\frac{5.4\vec{u}_\rho+7.2\vec{u}_\theta}{1.00-0.20t}\,\frac{\mathrm{m}}{\mathrm{s}^2}</math></center>
En forma escalar, hallamos el módulo,
En forma escalar, hallamos el módulo,
Línea 109: Línea 110:
El vector tangente a la trayectoria es el unitario en la dirección y sentido de la velocidad
El vector tangente a la trayectoria es el unitario en la dirección y sentido de la velocidad
-
<center><math>\vec{T}=\frac{\vec{v}}{|\vec{v}|}=\frac{-48\vec{u}_\rho+36\vec{u}_\varphi}{60}=-0.8\vec{u}_\rho+0.6\vec{u}_\varphi</math></center>
+
<center><math>\vec{T}=\frac{\vec{v}}{|\vec{v}|}=\frac{-48\vec{u}_\rho+36\vec{u}_\theta}{60}=-0.8\vec{u}_\rho+0.6\vec{u}_\theta</math></center>
Este vector forma un ángulo constante con la dirección radial.
Este vector forma un ángulo constante con la dirección radial.
Línea 115: Línea 116:
El vector normal es el unitario en la dirección y sentido de la aceleración normal
El vector normal es el unitario en la dirección y sentido de la aceleración normal
-
<center><math>\vec{N}=\frac{\vec{a}_n}{|\vec{a}_n|}=-\frac{5.4\vec{u}_\rho+7.2\vec{u}_\varphi}{9.0}=-0.6\vec{u}_\rho-0.8\vec{u}_\varphi</math></center>
+
<center><math>\vec{N}=\frac{\vec{a}_n}{|\vec{a}_n|}=-\frac{5.4\vec{u}_\rho+7.2\vec{u}_\theta}{9.0}=-0.6\vec{u}_\rho-0.8\vec{u}_\theta</math></center>
Es inmediato comprobar que este vector es ortogonal al anterior.
Es inmediato comprobar que este vector es ortogonal al anterior.

última version al 18:12 28 oct 2016

Contenido

1 Enunciado

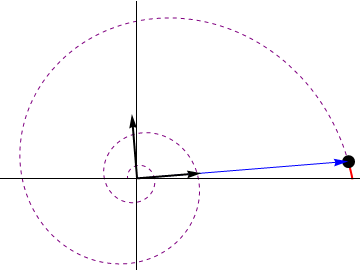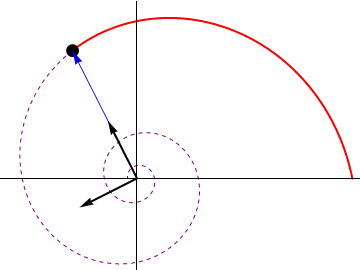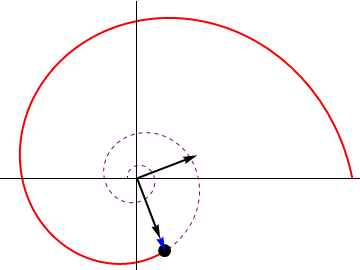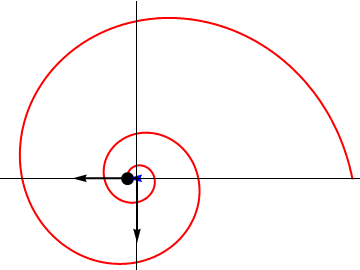
Una partícula describe una espiral logarítmica a partir de t = 0 de manera que, en el SI y empleando coordenadas polares,

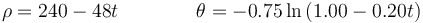
\rho = 240-48t\qquad\qquad \theta = -0.75\ln\left(1.00-0.20t\right)
  1. Halle la velocidad en cada instante.
  2. Calcule la rapidez del movimiento como función del tiempo.
  3. ¿Cuánto tiempo tarda la partícula en llegar al origen de coordenadas? ¿Cuántas vueltas alrededor del origen da en ese tiempo?
  4. Halle la aceleración para cada instante, así como sus componentes intrínsecas
  5. Calcule los vectores tangente y normal a la trayectoria en cada punto de ésta, en función de la base \{\vec{u}_\rho,\vec{u}_\theta\}
  6. Calcule el radio de curvatura como función del tiempo.

2 Velocidad instantánea

La fórmula para la velocidad en coordenadas polares viene dada por

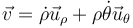
\vec{v} = \dot{\rho}\vec{u}_\rho + \rho\dot{\theta}\vec{u}_\theta

siendo en este caso

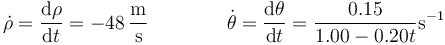
\dot{\rho} = \frac{\mathrm{d}\rho}{\mathrm{d}t} = -48\,\frac{\mathrm{m}}{\mathrm{s}}\qquad\qquad \dot{\theta}=\frac{\mathrm{d}\theta}{\mathrm{d}t}=\frac{0.15}{1.00-0.20t}\mathrm{s}^{-1}

lo que nos da la velocidad

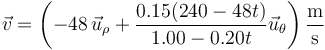
\vec{v}=\left(-48\,\vec{u}_\rho+\frac{0.15(240-48t)}{1.00-0.20t}\vec{u}_\theta\right)\frac{\mathrm{m}}{\mathrm{s}}

pero

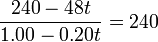
\frac{240-48t}{1.00-0.20t} = 240

así que queda simplemente

\vec{v}=(-48\vec{u}_\rho+36\vec{u}_\theta)\frac{\mathrm{m}}{\mathrm{s}}

Hay que señalar que esta velocidad depende del tiempo. Aunque las componentes son constantes, los vectores de la base son dependientes del tiempo, ya que van girando con la partícula en su movimiento.

Archivo:nautilus-03.gif

3 Rapidez instantánea

Una vez que tenemos la velocidad instantánea, calculamos la rapidez hallando su módulo.

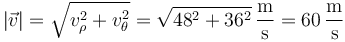
|\vec{v}| = \sqrt{v_\rho^2+v_\theta^2} = \sqrt{48^2+36^2}\,\frac{\mathrm{m}}{\mathrm{s}} = 60\,\frac{\mathrm{m}}{\mathrm{s}}

El movimiento es con rapidez constante y por tanto uniforme.

4 Tiempo de impacto

El tiempo en llegar al origen de coordenadas es aquel que hace ρ = 0. Esto ocurre para

240-48t_\mathrm{i} = 0\qquad\Rightarrow\qquad t = 5\,\mathrm{s}

El número de vueltas lo obtenemos calculando la variación en la coordenada θ. Cuando este ángulo varía en 2π quiere decir que se ha dado una vuelta. Si varía en 4π son dos vueltas y así sucesivamente. El número de vueltas total será

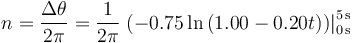
n = \frac{\Delta\theta}{2\pi}=\frac{1}{2\pi}\left.\left(-0.75\ln\left(1.00-0.20t\right)\right)\right|_{0\,\mathrm{s}}^{5\,\mathrm{s}}

Pero

\lim_{t\to 5\,\mathrm{s}}\ln(1.00-0.20t) = -\infty

Por tanto

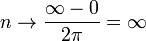
n \to \frac{\infty - 0}{2\pi} = \infty

Es decir, aunque tarda un tiempo finito en llegar al centro, da infinitas vueltas antes de hacerlo. La razón es que estas vueltas son cada vez más pequeñas y requieren menos tiempo.

5 Aceleración

5.1 En forma vectorial

La expresión de la aceleración en coordenadas polares es

\vec{a} = (\ddot{\rho}-\rho\dot{\theta}^2)\vec{u}_\rho+(\rho\ddot{\theta}+2\dot{\rho}\dot{\theta})\vec{u}_\theta

donde, en este caso

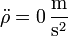
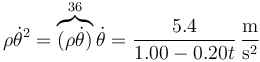
\ddot{\rho}=0\,\frac{\mathrm{m}}{\mathrm{s}^2}         \rho\dot{\theta}^2 = \overbrace{(\rho\dot{\theta})}^{36}\dot{\theta}=\frac{5.4}{1.00-0.20t}\,\frac{\mathrm{m}}{\mathrm{s}^2}        

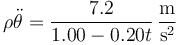
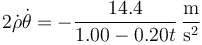
\rho\ddot{\theta} = \frac{7.2}{1.00-0.20t}\,\frac{\mathrm{m}}{\mathrm{s}^2}         2\dot{\rho}\dot{\theta} = -\frac{14.4}{1.00-0.20t}\,\frac{\mathrm{m}}{\mathrm{s}^2}

Reuniendo todo esto nos queda

\vec{a} = -\frac{5.4\vec{u}_\rho+7.2\vec{u}_\theta}{1.00-0.20t}\,\frac{\mathrm{m}}{\mathrm{s}^2}

En este caso particular, no obstante, hubiera sido más fácil calcular la aceleración como la derivada de la velocidad respecto al tiempo, aprovechando que las componentes de la velocidad son constantes.

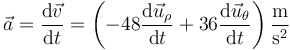
\vec{v}=(-48\vec{u}_\rho+36\vec{u}_\theta)\frac{\mathrm{m}}{\mathrm{s}}        \vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=\left(-48\frac{\mathrm{d}\vec{u}_\rho}{\mathrm{d}t}+36\frac{\mathrm{d}\vec{u}_\theta}{\mathrm{d}t}\right)\frac{\mathrm{m}}{\mathrm{s}^2}

donde

\frac{\mathrm{d}\vec{u}_\rho}{\mathrm{d}t} = \dot{\theta}\vec{u}_\theta=\left(\frac{0.15}{1.00-0.20t}\vec{u}_\theta\right)\frac{1}{\mathrm{s}}\qquad\qquad \frac{\mathrm{d}\vec{u}_\theta}{\mathrm{d}t} = -\dot{\theta}\vec{u}_\rho=-\left(\frac{0.15}{1.00-0.20t}\vec{u}_\rho\right)\frac{1}{\mathrm{s}}

lo que nos da la aceleración

\vec{a}=\frac{0.15}{1.00-0.20t}\left(-48\vec{u}_\theta-36\vec{u}_\rho\right)\frac{\mathrm{m}}{\mathrm{s}^2}=-\frac{5.4\vec{u}_\rho+7.2\vec{u}_\theta}{1.00-0.20t}\,\frac{\mathrm{m}}{\mathrm{s}^2}

5.2 Aceleración tangencial

Por tratarse de un movimiento uniforme, la aceleración tangencial es nula

a_t = \frac{\mathrm{d}|\vec{v}|}{\mathrm{d}t}=\frac{\mathrm{d}\ }{\mathrm{d}t}\left(60\,\frac{\mathrm{m}}{\mathrm{s}}\right)=0\,\frac{\mathrm{m}}{\mathrm{s}^2}

5.3 Aceleración normal

Si la aceleración tangencial es nula, toda la aceleración es normal, por lo que

\vec{a}_n = -\frac{5.4\vec{u}_\rho+7.2\vec{u}_\theta}{1.00-0.20t}\,\frac{\mathrm{m}}{\mathrm{s}^2}

En forma escalar, hallamos el módulo,

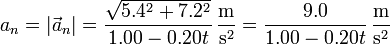
a_n = |\vec{a}_n| = \frac{\sqrt{5.4^2+7.2^2}}{1.00-0.20t}\,\frac{\mathrm{m}}{\mathrm{s}^2}=\frac{9.0}{1.00-0.20t}\,\frac{\mathrm{m}}{\mathrm{s}^2}

6 Vectores tangente y normal

6.1 Vector tangente

El vector tangente a la trayectoria es el unitario en la dirección y sentido de la velocidad

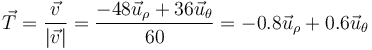
\vec{T}=\frac{\vec{v}}{|\vec{v}|}=\frac{-48\vec{u}_\rho+36\vec{u}_\theta}{60}=-0.8\vec{u}_\rho+0.6\vec{u}_\theta

Este vector forma un ángulo constante con la dirección radial.

6.2 Vector normal

El vector normal es el unitario en la dirección y sentido de la aceleración normal

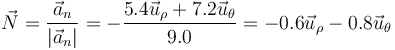
\vec{N}=\frac{\vec{a}_n}{|\vec{a}_n|}=-\frac{5.4\vec{u}_\rho+7.2\vec{u}_\theta}{9.0}=-0.6\vec{u}_\rho-0.8\vec{u}_\theta

Es inmediato comprobar que este vector es ortogonal al anterior.

7 Radio de curvatura

Una vez que tenemos la aceleración normal y la rapidez hallamos el radio de curvatura como

R = \frac{|\vec{v}|^2}{a_n}=\frac{(60\,\mathrm{m}/\mathrm{s})^2}{(9.0/(1.00-0.20t))\mathrm{m}/\mathrm{s}^2}=80(1.00-0.20t)\,\mathrm{m}=(80-16t)\,\mathrm{m}

El radio de curvatura disminuye linealmente con el tiempo hasta anularse cuando la partícula llega al centro de la espiral.

Obtenido de "http://tesla.us.es/wiki/index.php/Espiral_logar%C3%ADtmica_(GIE)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 18:12, 28 oct 2016. - Esta página ha sido visitada 4.060 veces. - Aviso legal - Acerca de Laplace